Question 1. Calculate the amount and compound interest on
(i) Rs 10,800 for 3 years at 12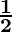 % per annum compounded annually.
% per annum compounded annually.
(ii) Rs 18,000 for 2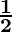 years at 10% per annum compounded annually.
years at 10% per annum compounded annually.
(iii) Rs 62,500 for 1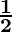 years at 8% per annum compounded half-yearly.
years at 8% per annum compounded half-yearly.
(iv) Rs 8,000 for 1 year at 9% per annum compounded half-yearly.
(v) Rs 10,000 for 1 year at 8% per annum compounded half-yearly.
Solution:
(i) Given values are,
P = Rs 10,800
R = 12 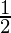 % per annum =
% per annum = 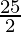 %
%
T = 3 Years
As it is compounded annually then, n = 3 times.
We have,
A = P (1 +  )n
)n
A = 10,800 (1+ 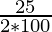 )3
)3
A = 10,800 (1+ 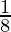 )3
)3
A = 10,800 (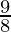 )3
)3
A = Rs 15,377.34
CI = A – P
CI = 15,377.34 – 10,800
CI = Rs 4,577.34
Hence, the amount = Rs 15,377.34 and
Compound interest = Rs 4,577.34
(ii) Given values are,
P = Rs 18,000
R = 10 % per annum
T = 2 Years
Years
As it is compounded annually then, n = 2 times.
times.
We have,
A = P (1 +  )n
)n
A = 18,000 (1+ 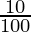 )2½
)2½
What we will do here is Firstly we know 2 Years is 2 years and 6 months which can be calculated by first calculating the amount to 2 years using CI formula and then calculating the simple interest by using SI formula.
Years is 2 years and 6 months which can be calculated by first calculating the amount to 2 years using CI formula and then calculating the simple interest by using SI formula.
The amount for 2 years has to be calculated :
A = 18,000 (1+ 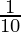 )2
)2
A = 18,000 (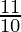 )2
)2
A = Rs 21,780
CI = A – P
CI = 21,780 – 18,000
CI = Rs 3,780
Now, The amount for  year has to be calculated:
year has to be calculated:
New P is equal to the amount after 2 Years. Hence,
P = Rs 21,780
R = 10 % per annum
T =  year
year
SI = 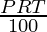
SI = 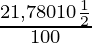
SI = 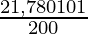
SI = Rs 1,089
Hence, the Total amount = A + SI
= 21,780 + 1,809
= Rs 22,869
Total compound interest = CI + SI
= 3,780 + 1,809
= Rs 4,869
(iii) Given values are,
P = Rs 62,500
R = 8 % per annum hence 4% Half Yearly
T = 1 Years
Years
As it is compounded Half yearly then, n = 3 times. (1 Years contains 3 half years)
Years contains 3 half years)
We have,
A = P (1 +  )n
)n
A = 62,500 (1+ 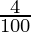 )3
)3
A = 62,500 (1+ 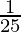 )3
)3
A = 62,500 (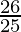 )3
)3
A = Rs 70,304
CI = A – P
CI = 70,304 – 62,500
CI = Rs 7,804
Hence, the amount = Rs 70,304 and
Compound interest = Rs 7,804
(iv) Given values are,
P = Rs 8,000
R = 9 % per annum hence, 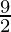 % Half Yearly
% Half Yearly
T = 1 Year
As it is compounded Half yearly then, n = 2 times. (1 Year contains 2 half years)
We have,
A = P (1 +  )n
)n
A = 8,000 (1+ 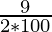 )2
)2
A = 8,000 (1+ 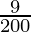 )2
)2
A = 8,000 (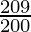 )2
)2
A = Rs 8,736.20
CI = A – P
CI = 8,736.20 – 8,000
CI = Rs 736.20
Hence, the amount = Rs 8,736.20 and
Compound interest = Rs 736.20
(v) Given values are,
P = Rs 10,000
R = 8 % per annum hence, 4% Half Yearly
T = 1 Year
As it is compounded Half yearly then, n = 2 times. (1 Year contains 2 half years)
We have,
A = P (1+  )n
)n
A = 10,000 (1+ (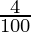 ))2
))2
A =10,000 (1+ (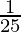 ))2
))2
A = 10,000 (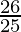 )2
)2
A = Rs 10,816
CI = A – P
CI = 10,816- 10,000
CI = Rs 816
Hence, the amount = Rs 10,816 and
Compound interest = Rs 816
Question 2. Kamala borrowed Rs 26,400 from a Bank to buy a scooter at a rate of 15% p.a. compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan?
Solution:
Here, Given values are,
P = Rs 26,400
R = 15 % per annum
T = 2 Years and 4 months, which is 2 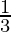 years
years
As it is compounded annually then, n = 2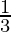 times
times
We have,
A = P (1 +  )n
)n
A = 26,400 (1 + (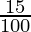 )2(1/3)
)2(1/3)
What we will do here is Firstly 2 years and 4 months which can be calculated by first calculating the amount to 2 years using CI formula and then calculating the simple interest by using SI formula.
The amount for 2 years has to be calculated:
A = 26,400 (1+ (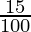 )2
)2
A = 26,400 (1+ (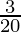 )2
)2
A = 26,400 (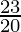 )2
)2
A = Rs 34,914
Now, The amount for (1/3) year (4 months) has to be calculated :
New P is equal to the amount after 2 Years. Hence,
P = Rs 34,914
R = 15 % per annum
T = 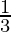 year
year
SI = 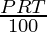
SI = 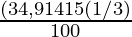
SI = 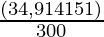
SI = 1,745.70
Hence, the Total amount = A + SI
= 34,914 + 1,745.70
= Rs 36,659.70
Hence, the amount to be paid by Kamla = ₹ 36,659.70
Question 3. Fabina borrows Rs 12,500 at 12% per annum for 3 years at simple interest and Radha borrows the same amount for the same time period at 10% per annum, compounded annually. Who pays more interest and by how much?
Solution:
Let’s see each case
Fabina Case: at simple interest
P = 12,500
R = 12% per annum
T = 3 Years
SI = 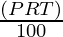
SI = 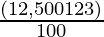
SI = Rs 4,500
Radha Case: at compound interest
P = 12,500
R = 10% per annum
T = 3 Years
As it is compounded annually then, n = 3 times
We have,
A = P (1 +  )n
)n
A = 12,500 (1 + (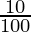 ))3
))3
A =12,500 (1 + 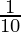 )3
)3
A = 12,500 (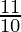 )3
)3
A = Rs 16,637.5
CI = A – P
CI = 16,637.5 – 12,500
CI = 4,137.5
Clearly we can see that Fabina paid more interest, and she paid
4,500 – 4,137.5 = Rs 362.5 more than Radha
Question 4. I borrowed Rs 12,000 from Jamshed at 6% per annum simple interest for 2 years. Had I borrowed this sum at 6% per annum compound interest, what extra amount would I have to pay?
Solution:
Lets see each case First
At simple interest
P = 12,000
R = 6% per annum
T = 2 Years
SI = 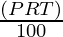
SI = 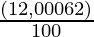
SI = Rs 1,440
At compound interest
P = 12,000
R = 6% per annum
T = 2 Years
As it is compounded annually then, n = 2 times
We have,
A = P (1 +  )n
)n
A = 12,000 (1+ (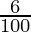 ))2
))2
A =12,000 (1+ (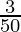 ))2
))2
A = 12,000 (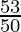 )2
)2
A = Rs 13,483.2
CI = A – P
CI = 13,483.2 – 12,000
CI = 1,483.2
Clearly we can see that,
1,483.2 – 1,440 = Rs 43.2
Hence, the extra amount to be paid = ₹ 43.20
Question 5. Vasudevan invested Rs 60,000 at an interest rate of 12% per annum compounded half-yearly. What amount would he get
(a) after 6 months?
(b) after 1 year?
Solution:
Let’s see each case
(a)
P = 60,000
R = 12% per annum (6% Half yearly)
T = 6 Months
As it is compounded Half Yearly then, n = 1 times (as 6 months is 1 half year)
We have,
A = P (1 +  )n
)n
A =60,000 (1+ (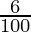 ))1
))1
A =60,000 (1+ (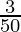 ))1
))1
A = 60,000 (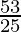 )1
)1
A = Rs 63,600
He would get Rs 63,600 after 6 Months.
(b)
P = 60,000
R = 12% per annum (6% Half yearly)
T = 1 Year
As it is compounded Half Yearly then, n = 2 times (as 1 Year is 2 half year)
We have,
A = P (1 +  )n
)n
A = 60,000 (1+ (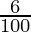 ))2
))2
A = 60,000 (1+ (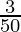 ))2
))2
A = 60000 (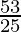 )2
)2
A = Rs 67,416
He would get Rs 67,416 after 1 Year.
Question 6. Arif took a loan of Rs 80,000 from a bank. If the rate of interest is 10% per annum, find the difference in amounts he would be paying after 1 years if the interest is
years if the interest is
(a) compounded annually.
(b) compounded half-yearly.
Solution:
Let’s see each case
(a) Compounded Annually
P = 80,000
R = 10% per annum
T = 1 Year
Year
As it is compounded annually then, n = 1  times
times
We have,
A = P (1 +  )n
)n
A = 80,000 (1 + (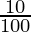 )1½
)1½
What we will do here is Firstly we know 1 Years is 1 year and 6 months which can be calculated by first calculating the amount to 1 year using CI formula and then calculating the simple interest by using SI formula.
Years is 1 year and 6 months which can be calculated by first calculating the amount to 1 year using CI formula and then calculating the simple interest by using SI formula.
The amount for 1 years has to be calculated :
A = 80,000 (1+ (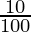 ))1
))1
A = 80,000 (1+ (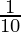 )1
)1
A = 80,000 (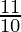 )1
)1
A = Rs 88,000
Now, The amount for  Year (6 months) has to be calculated :
Year (6 months) has to be calculated :
New P is equal to the amount after 1 Year. Hence,
P = Rs 88,000
R = 10 % per annum
T = Year
Year
SI = 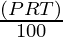
SI = 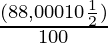
SI = 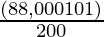
SI = 4,400
Hence, the Total amount = A + SI
= 88,000 + 4,400
= Rs 92,400
(b) Compounded Half-yearly
P = 80,000
R = 10% per annum (5 % Half Yearly)
T = 1 Year
Year
As it is compounded annually then, n = 3 times (as 1 Year is 3 half year)
Year is 3 half year)
We have,
A = P (1 +  )n
)n
A = 80,000 (1+ (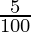 )3
)3
A = 80,000 (1+ (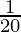 )3
)3
A = 80,000 (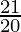 )3
)3
A = Rs 92,610
Hence, the Total amount = Rs 92,610
Question 7. Maria invested Rs 8,000 in a business. She would be paid interest at 5% per annum compounded annually. Find
(a) The amount credited against her name at the end of the second year.
(b) The interest for the 3rd year.
Solution:
Let’s see each case
Here,
P = 8,000
R = 5% Per annum
(a) The amount credited against Maria’s name at the end of the second year.
T = 2 Year
As it is compounded annually then, n = 2 times
We have,
A = P (1 +  )n
)n
A = 8,000 (1+ (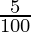 ))2
))2
A = 8,000 (1+ (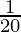 ))2
))2
A = 8,000 (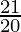 )2
)2
A = Rs 8,820
Hence, the amount credited against Maria’s name at the end of the second year = Rs 8,820
(b) The interest for the 3rd year.
T = 3 Year
As it is compounded annually then, n = 3 times
We have,
A = P (1+  )n
)n
A = 8,000 (1+ (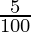 ))3
))3
A = 8,000 (1+ (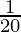 ))3
))3
A = 8,000 (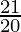 )3
)3
A = Rs 9,261
The interest for the 3rd year = Amount after 3 years – Amount after 2 Years
= 9,261 – 8,820
= Rs 441
Another Solution for (b)
As we can calculate interest of 3rd year by having 2nd Year Amount as P.
P = 8,820
R = 5% per annum
T = 1 Year (2nd to 3rd year)
SI = 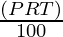
SI = 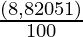
SI = Rs 441
The interest for the 3rd year = Rs 441
Question 8. Find the amount and the compound interest on Rs 10,000 for 1 years at 10% per annum, compounded half-yearly. Would this interest be more than the interest he would get if it was compounded annually?
years at 10% per annum, compounded half-yearly. Would this interest be more than the interest he would get if it was compounded annually?
Solution:
Let’s see each cases
Compounded Annually
P = 10,000
R = 10% per annum
T = 1 Year
Year
As it is compounded annually then, n = 1  times
times
We have,
A = P (1 +  )n
)n
A = 10,000 (1 + (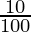 )1½
)1½
What we will do here is Firstly we know 1½ Years is 1 year and 6 months which can be calculated by first calculating the amount to 1 year using CI formula and then calculating the simple interest by using SI formula.
The amount for 1 year has to be calculated:
A = 10,000 (1 + 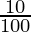 )1
)1
A = 10,000 (1+ 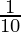 )1
)1
A = 10,000 (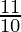 )1
)1
A = Rs 11,000
CI = A – P
CI = 11,000-10,000
CI = 1,000
Now, The amount for  Year (6 months) has to be calculated :
Year (6 months) has to be calculated :
New P is equal to the amount after 1 Year. Hence,
P = Rs 11,000
R = 10 % per annum
T = Year
Year
SI = 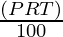
SI = 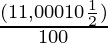
SI = 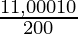
SI = 550
Hence, the Total Interest (compounded annually)= CI + SI
= 1,000 + 550
= Rs 1,550
Compounded Half-yearly
P = 10,000
R = 10% per annum (5 % Half Yearly)
T = 1 Year
Year
As it is compounded annually then, n = 3 times (as 1 Year is 3 half year)
Year is 3 half year)
We have,
A = P (1 +  )n
)n
A = 10,000 (1 + (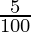 )3
)3
A = 10,000 (1+ 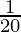 )3
)3
A = 10,000 (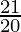 )3
)3
A = Rs 11,576.25
CI = A – P
CI = 11,576.25 – 10,000
CI = 1,576.25
Hence, the Total Interest (compounded Half Yearly) = Rs 11576.25
Difference between the two interests = 1,576.25 – 1,550 = Rs 26.25
Hence, the interest will be Rs 26.25 more when compounded half-yearly than the interest when compounded annually.
Question 9. Find the amount which Ram will get on Rs 4096, if he gave it for 18 months at 12  % per annum, interest being compounded half-yearly.
% per annum, interest being compounded half-yearly.
Solution:
Let’s see this case
P = Rs 4,096
R = 12  % per annum (
% per annum (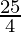 % Half yearly)
% Half yearly)
T = 18 Months = 1 Year
Year
As it is compounded Half yearly then, n = 3 Times
We have,
A = P (1 +  )n
)n
A = 4,096 (1+ (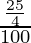 )3
)3
A = 4,096 (1+ 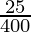 )3
)3
A = 4,096 (1+ (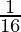 )3
)3
A = 4,096 (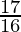 )3
)3
A = Rs 4,913
Ram will get the amount = Rs 4,913
Question 10. The population of a place increased to 54,000 in 2003 at a rate of 5% per annum
(a) find the population in 2001.
(b) what would be its population in 2005?
Solution:
Here,
P = 54,000 (in 2003)
R = 5% per annum
(a) Population in 2001
T = 2 Years (back)
n = 2
Population in 2003 = Population in 2001 (1 +  )n
)n
54,000 = P1 (1+(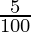 ))2
))2
54,000 = P1 (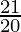 )2
)2
54,000 = P1 (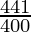 )
)
P1 = 54,000 (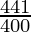 )
)
P1 = 48,979.59
P1 = 48,980 (approx.).
Population in 2001 was 48,980 (approx.).
(b) Population in 2005
T = 2 Years
n = 2
We have,
A = P (1 +  )n
)n
A = 54,000 (1+ 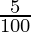 )2
)2
A = 54,000 (1+ (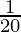 )2
)2
A = 54,000 (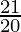 )2
)2
A = 59,535
Population in 2005 will be 59,535
Question 11. In a Laboratory, the count of bacteria in a certain experiment was increasing at the rate of 2.5% per hour. Find the bacteria at the end of 2 hours if the count was initially 5, 06,000.
Solution:
Here,
P = 5,06,000
R = 2.5% per hour
T = 2 hours
We have,
A = P (1 +  )n
)n
A = 5,06,000 (1+ 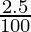 )2
)2
A = 5,06,000 (1+ 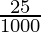 )2
)2
A = 5,06,000 (1+ 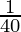 )2
)2
A = 5,06,000 (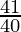 )2
)2
A = 5,31,616.25
A = 5,31,616 (approx.)
Bacteria at the end of 2 hours = 5,31,616 (approx.)
Question 12. A scooter was bought at Rs 42,000. Its value depreciated at the rate of 8% per annum. Find its value after one year.
Solution:
Here,
P = 42,000
R = 8% per annum (depreciated)
T = 1 Year
We have,
A = P (1 +  )n
)n
A = 42,000 (1- 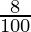 )1 (negative sign because the price is reduced)
)1 (negative sign because the price is reduced)
A = 42,000 (1- (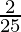 )1
)1
A = 42,000 (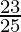 )1
)1
A = Rs 38,640
The value of scooter after one year will be = Rs 38,640
Share your thoughts in the comments
Please Login to comment...