Given ellipse: 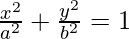
Its major axis is the x-axis
Using parametric form of ellipse, x = acosθ, y = bsinθ,
If coordinates of A are (acosθ, bsinθ)
Then B’S coordinates will be (acosθ, -bsin θ).
Now, OC = a, OD = acos θ, so CD = a(1 + cos θ)
AB = |AD| + |BD| = 2b sin θ
Area of △ABC = 1/2.AB.CD
= 1/2.2bsin θ.a(1 + cos θ)
△(θ) = ab.sinθ.(1 + sin θ)
For maxima/minima, put △'(θ) = 0
△'(θ) = ab[cosθ[1 + cosθ] + sinθ[-sinθ]]
△'(θ) = ab[2cos2θ + cosθ – 1] = 0
2cos2θ + cosθ – 1 = 0
2cos2θ + 2cosθ – cosθ – 1 = 0
2cosθ(cosθ + 1) – 1(cosθ + 1) = 0
(2cosθ – 1).(cosθ + 1) = 0
cosθ = 1/2 or cosθ = -1
If cosθ = -1, then sinθ = 0 & △(θ) = 0
But if cosθ = 1/2, sinθ = √3/2 & △(θ) = ab.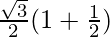
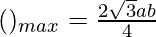
Let the length of the rectangle = x
the breadth of the rectangle = y
and the radius of the semicircle = x/2
So given that total perimeter of the window = 10m
P = πx/2 + x + 2y = 10
x(1 + π/2) + 2y = 10
2y = 10 – x(1 + π/2)
y = 5 – x(1/2 – π/4) -(1)
Now, the area of the window
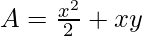 -(2)
-(2)
From eq(1) put the value of y in eq(2), we get
![Rendered by QuickLaTeX.com A=x.[5 - x(\frac{1}{2} - \frac{π}{4})]+\frac{πx^2}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0b12944506204feee148b6c09590ba8d_l3.png)
= 5x – x2(1/2 + π/4) + πx2/8
On differentiating we get
A’ = 5 – 2x(1/2 + π/4) + 2xπ/8
= 5 – x(1 + π/2) + xπ/4
Put A’ = 0
5 – x(1 + π/2) + xπ/4 = 0
-x(1 + π/2) + xπ/4 = -5
x(-1 – π/2 + π/4) = -5
x(-1 – π/2 + π/4) = -5
x(1 + π/4) = 5
x = 5/ (1 + π/4)
x = 20/ π + 4
Hence, the length of the rectangle = 20/ π + 4
Now put the value of x in eq(1)
y = 5 – (20/ π + 4)(1/2 – π/4)
y = 10/π + 4
Hence, breadth of the rectangle = 10/π + 4
and the radius of the semicircle = x/2 = 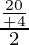 = 10/π + 4
= 10/π + 4
Question 9. A point on the hypotenuse of a triangle is at distance a and b from the sides of the triangle. Show that the minimum length of the hypotenuse is 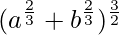
Solution:

Given, a triangle ABC
Let, PE = a & PD = b
In the △ABC, ∠B = 90
Let ∠C = θ, so, ∠ DPA = θ
DP|| BC.
Now in △ADDP,
cosθ = DP/AP = b/AP
AP = b/cosθ
In △EPC,
sinθ = EP/CP = a/CP
CP = a/sin θ
Now AC = h = PA + PC
h = 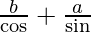
h(θ) = b sec θ + a cosec θ
Put h'(θ) = 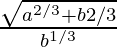
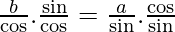
b sin3θ = a cos 3θ
tan3θ = a/b
tanθ = (a/b)1/3
secθ = 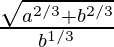
cosecθ = 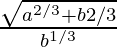
hmax = 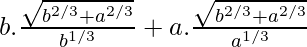
hmax = (b2/3+a2/3)3/2
Question 10. Find the points at which the function f given by f (x) = (x – 2)4 (x + 1)3 has
(i) local maxima
(ii) local minima
(iii) point of inflexion
Solution:
f(x) = (x – 2)4(x + 1)3
On differentiating w.r.t x, we get
f'(x) = 4(x – 2)3(x + 1)3 + 3(x + 1)2(x – 2)4
Put f'(x) = 0
(x – 2)3(x + 1)2 [4(x + 1) + 3(x – 2)] = 0
(x – 2)3(x + 1)2(7x – 2) = 0
Now,
Around x = -1, sign does not change, i.e
x = -1 is a point of inflation
Around x = 2/7, sign changes from +ve to -ve i.e.,
x = 2/7 is a point of local maxima.
Around x = 2, sign changes from -ve to +ve i.e.,
x = 2 is a point of local minima
Question 11. Find the absolute maximum and minimum values of the function f given by f(x) = cos2 x + sin x, x ∈ [0, π]
Solution:
f(x) = cos2x + sin x; x ϵ [0, π]
On differentiating w.r.t x, we get
f'(x) = 2cos x(-sin x) + cos x = cos x – sin2x
Put f'(x) = 0
cos x(1 – 2sin x) = 0
cos x = 0; sin x = 1/2
In x ϵ[0, π] if cos x = 0, then x = π/2
and if sin x = 1/2, then x = π/6 & 5π/6
Now, f”(x) = -sin x – 2 cos2x
f”(π/2) = -1 + 2 = 1 > 0
x = π/2 is a point of local minima f(π/2) = 1
f”(π/6) = 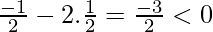
x = π/6 is a point of local maxima f(π/6) = 5/4
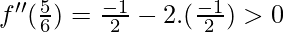
x = 5π/6 is a point of local minima f(5π/6) = 5/4
Global/Absolute maxima = ma{f(0), f(π/6), f(π)}
= max{1, 5/4, 1}
= 5/4 = Absolute maxima value
Global/Absolute minima = min{f(0), f(π/2), f(π/6), f(π)}
= min{1, 1, 5/4, 1}
= 1 = Absolute minima value
Question 12. Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is 4π/3
Solution:
Let ABC be the cone
and o is the centre of the sphere.
AO = BO = CO = R
AO = h = height of cone
BD = CD = r = radius of cone.
∠DOC = θ -(Properties of circle)
In △ DOC,
OD = R cosθ & CD = Rsinθ,
r = R sin θ
AD = AO + OD = R + Rcosθ
h = R(1 + cosθ)
Now, the volume of the cone is
V = 
v(θ) = 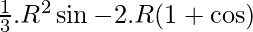
![Rendered by QuickLaTeX.com v'(θ)=\frac{}{}[\sin{-2}θ(-\sinθ)+(1+\cosθ)(2\sinθ\cosθ)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1112b88901bd66ec7466a7bc8afe0c1e_l3.png)
Put v(θ) = 0
sinθ[2cosθ + 2cos2θ − sin2θ] = 0
sinθ[2cosθ + 2cos2θ − 1] = 0
sinθ(3cosθ − 1)(1 + cosθ) = 0
sinθ = 0, cos = 1/3, cosθ = −1
If sinθ = 0, then volume will be 0.
If cosθ = -1, then sinθ = 0 & again volume will be 0.
But if cosθ = 1/3; sinθ = 2√2/3 and
Volume, v = 32/81πR3, which is maximum.
Height, h = R(1 + cosθ) = R(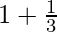 )
)
h = 4r/3
Hence proved
Question 13. Let f be a function defined on [a, b] such that f′(x) > 0, for all x ∈ (a, b). Then prove that f is an increasing function on (a, b).
Solution:
Given that on [a, b] f'(x) > 0, for all x in interval I.
So let us considered x1, x2 belongs to I with x1 < x2
To prove: f(x) is increasing in (a, b)
According to the Lagrange’s Mean theorem
f(x2) – f(x1)/ x2 – x1 = f'(c)
f(x2) – f(x1) = f'(c)(x2 – x1)
Where x1 < c < x2
As we know that x1 < x2
so x1 < x2 > 0
It is given that f'(x) > 0
so, f'(c) > 0
Hence, f(x2) – f(x1) > 0
f(x2) < f(x1)
Therefore, for every pair of points x1, x2 belongs to I with x1 < x2
f(x2) < f(x1)
f(x) is strictly increasing in I
Question 14. Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 2R/√3. Also, find the maximum volume.
Solution:
In △ABC,
AC2 = BC2 + AB2
4R2 = 4r2 + h2
r2 = R2–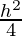 ……….(1)
……….(1)
Now, volume of cylinder = πr2h
Put the value ov r2 from eq(1), we get
V = π(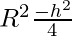 ).h
).h
V(h) = 
On differentiating both side we get
V ‘(h) = 
Now, put V'(h) = 0
πR2 = 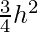
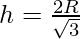
Now the maximum volume of cylinder = π[R2. 2R/√3 – 1/4.4R2/3.2R/√3]
= 4πR3/ 3√3
Question 15. Show that the height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi-vertical angle α is one-third that of the cone and the greatest volume of the cylinder is 4/27πh3tan2α.
Solution:

Let,
XQ = r
XO = h’
AO = h
OC = r’
∠XAQ = α
In triangle AXQ and AOC = XQ/OC = AX/AO
So, r’/r = h-h’/h
hr’ = r(h-h’)
hr’ = rh – rh’
rh’ = rh – hr’
rh’ = h(r – r’)
h’ = h(r – r’)/r
The volume of cylinder = πr’2h’
v = πr’2(h(r – r’)/r)
= π(h(rr’2 – r’3)/r)
On differentiating we get
v’ = πh/r(2rr’ – 3r’2)
Again on differentiating we get
v” = πh/r(2r – 6r’) ………(1)
Now put v’ = 0
πh/r(2rr’ – 3r’2) = 0
(2rr’ – 3r’2) = 0
2r’r = 3r’2
r’ = 2r/3
So, v is maximum at r’ = 2r/3
The maximum volume of cylinder = πh/r[r. 4r2/9 – 8r2/27]
= πhr2[4/27]
= 4/27πh(h tanα)2
= 4/27πh3 tan2α
Question 16. A cylindrical tank of a radius 10 m is being filled with wheat at the rate of 314 cubic meters per hour. Then the depth of the wheat is increasing at the rate of
(A) 1 m/h (B) 0.1 m/h (C) 1.1 m/h (D) 0.5 m/h
Solution:
Given,
Radius of cylinder = 10m [radius is fixed]
Rate of increase of volume = 314m3/h
ie dv/dt = 314m3/h
Now, the volume of cylinder = πr2h
v = π.(10)2.h
v = 100πh
On differentiating w.r.t t, we get
dv/dt = 100π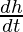
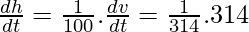
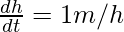
So option A is correct
Deleted Questions
Using differentials, find the approximate value of each of the following:
(i) (17/81)1/4
(ii) 33-1/5
Solution:
(i) (17/81)1/4
Let y = x1/4, x = 16/81 and △x = 1/81
△y = (x + △x)1/4 – x1/4
= (17/81)1/4 – (16/81)1/4
= (17/81)1/4 – (2/3)
So,
(17/81)1/4 = (2/3) + △y
Here, dy is approximately equal to △y
dy = (dy/dx)△x
= 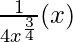
= 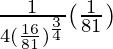
= 27/32 × 1/81
= 1/96
= 0.010
Hence, the approximate value of (17/81)1/4 = 2/3 + 0.010 = 0.677
(ii) 33-1/5
Let y = x-1/5, x = 32 and △x = 1
△y = (x + △x)-1/5 – x-1/5
= (33)-1/5 – (32)-1/5
= (33)-1/5 – 1/2
So,
(33)-1/5 = 1/2 + △y
Here, dy is approximately equal to △y
dy = (dy/dx)△x
= 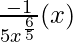
= 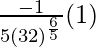
= -1/320
= -0.003
Hence, the approximate value of (33)-1/5 = 1/2 – 0.003 = 0.497
Find the equation of the normal to curve x2 = 4y which passes through the point (1, 2).
Solution:
Given area: x2 = 4y
On Differentiating both sides with respect to y,
2x(dx/dy) = 4
dx/dy = 2/x
Slope = -1/m = -2/x
By point slope form equation of normal will be,
y – 2 = -1(x – 1)
x + y = 3 is the required equation of normal.
Show that the normal at any point θ to the curve x = acosθ + aθsinθ, y = asinθ – aθ cosθ is at a constant distance from the origin.
Solution:
Given curve,
x = acosθ + aθsin θ
y = asinθ – aθcos θ
Now -dx/dy = slope of normal =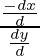 -(1)
-(1)
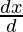 = -asinθ + asinθ + aθcosθ
= -asinθ + asinθ + aθcosθ
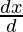 = aθcosθ -(2)
= aθcosθ -(2)
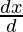 = acosθ + aθsinθ – acosθ
= acosθ + aθsinθ – acosθ
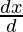 = aθsinθ -(3)
= aθsinθ -(3)
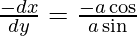 -(From 1, 2 & 3)
-(From 1, 2 & 3)
-dx/dy = -cotθ
Now using point slope from, equation of normal will be,
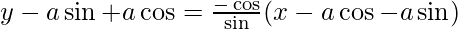
ysinθ – asin-2θ + aθcosθsinθ = -xcosθ + acos2θ + aθsinθcosθ
ysinθ + ysinθ − a = 0
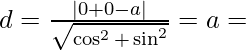 constant.
constant.
Hence proved
The slope of the tangent to the curve x = t2 + 3t – 8, y = 2t2 – 2t – 5 at the point (2,– 1) is
(A) 22/7 (B) 6/7 (C) 7/6 (D) -6/7
Solution:
Given that the slope of the tangent to the curve x = t2 + 2t – 8 and y = 2t2 – 2t – 5
On differentiating we get
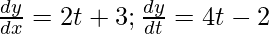
Now, when x = 2,
t2 + 3 – 8 = 2
t2 + 3 – 10 = 0
t2 – 2t + 5t – 10 = 0
(t – 2)(t + 5) = 0
Here, t = 2, t = -5 ……….(1)
When y = -1
2t2 – 2t – 5 = -1
2t2 – 2t – 4 = 0
t2 – t – 2 = 0
(t + 1)(t – 2) = 0
t = -1 or t = 2 ……….(2)
From eq(1) & eq(2) satisfies both,
Now, 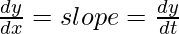
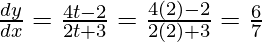
So, option B is the correct.
The line y = mx + 1 is a tangent to the curve y2 = 4x if the value of m is
(A) 1 (B) 2 (C) 3 (D)1/2
Solution:
The curve if y2 = 4x …….(1)
On differentiating we get

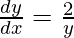
The slope of the tangent to the given curve at point(x, y)
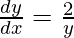
m = 2/y
y = 2/m
The equation of line is y = mx + 1
Now put the value of y, we get the value of x
2/m = mx + 1
x = 2 – m/m
Now put the value of y and x in eq(1), we get
(2/m)2 = 4(2 – m/m)
m = 1
Hence, the option A is correct
The normal at the point (1, 1) on the curve 2y + x2 = 3 is
(A) x + y = 0 (B) x – y = 0
(C) x + y +1 = 0 (D) x – y = 1
Solution:
The equation of curve 2y + x2 = 3
On differentiating w.r.t x, we get
2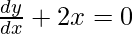
dy/dx = -x
The slope of the tangent to the given curve at point(1, 1)
dy/dx = -x = -1
m = -1
And slope of normal = 1
Now the equation of normal
(y -1) = 1(x – 1)
x – y = 0
So, B option is correct
The normal to the curve x2 = 4y passing (1, 2) is
(A) x + y = 3 (B) x – y = 3 (C) x + y = 1 (D) x – y = 1
Solution:
The equation of curve is x2 = 4y …….(1)
On differentiating w.r.t x, we get
2x = 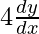
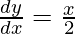
The slope of normal at (x, y)
-dx/dy = -2/x = m
The slope at given point(1, 2)
m = (y – 2)/(x – 1)
-2/x = (y – 2)/(x – 1)
y = 2/x
Now put the value of y in eq(1)
x2 = 4(2/x)
x = 2
and y = 1
So the point is (2, 1)
Now the slope of normal at point(2, 1) = -2/2 = -1
The equation of the normal is
(y – 1) = -1(x – 2)
x + y = 3
So option A is correct
The points on the curve 9y2 = x3, where the normal to the curve makes equal intercepts with the axes are
(A) 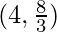 (B)
(B) 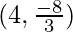
(C) (D)
(D)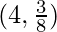
Solution:
Given equation 9y2 = x3
On differentiating w.r.t x, we get
18y dy/dx = 3x2
dy/dx = 3x2/18y
dy/dx = x2/6y
Now, the slope of the normal to the given curve at point (x1, y1) is
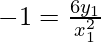
Hence, the equation of the normal to the curve at point (x1, y1) is
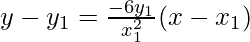
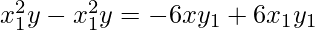
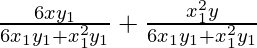
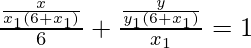
According to the question it is given that the normal
make equal intercepts with the axes.
So,
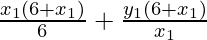
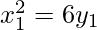 …………(1)
…………(1)
The point (x1, y1)lie on the curve,
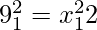 …………(2)
…………(2)
From eq(1) and (2), we get

From eq(2), we get
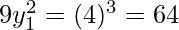

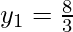
Hence, the required points are 
So, option A is correct.
Share your thoughts in the comments
Please Login to comment...