Question 1. Find the maximum and minimum values, if any, of the following function given by
(i) f(x) = (2x – 1)2 + 3
Solution:
Given that, f(x) = (2x – 1)2 + 3
From the given function we observe that
(2x – 1)2 ≥ 0 ∀ x∈ R,
So,
(2x – 1)2 + 3 ≥ 3 ∀ x∈ R,
Now we find the minimum value of function f when 2x-1 = 0
So, x = 1/2
f = f(1/2) = (2(1/2) – 1)2 + 3 = 3
Hence, the minimum value of the function is 3 and this function does not contain maximum value.
(ii) f(x) = 9x2 + 12x + 2
Solution:
Given that, f(x) = 9x2 + 12x + 2
we can also write as f(x) = (3x + 2)2 – 2
From the given function we observe that
(3x + 2)2 ≥ 0 ∀ x∈ R,
So,
(3x + 2)2 – 2 ≥ 2 ∀ x∈ R,
Now we find the minimum value of function f when 3x + 2 = 0
So, x = -2/3
f = f(-2/3) = (3(-2/3) + 2)2 – 2 = -2
Hence, the minimum value of the function is -2 and this function does not contain maximum value.
(iii) f(x) = -(x – 1)2 + 10
Solution:
Given that, f(x) = -(x – 1)2 + 10
From the given function we observe that
(x – 1)2 ≥ 0 ∀ x∈ R,
So,
-(x – 1)2 + 10 ≤ 10 ∀ x∈ R,
Now we find the maximum value of function f when x – 1 = 0
So, x = 1
f = f(1) = -(1 – 1)2 +10 = 10
Hence, the maximum value of the function is 10 and this function does not contain minimum value.
(iv) g(x) = x3 + 1
Solution:
Given that, g(x) = x3 + 1
When x —> ∞, then g(x) —> ∞
When x —> -∞, then g(x) —> -∞
So, this function has neither minimum nor maximum value
Question 2. Find the maximum and minimum values, if any, of the following functions given by
(i) f(x) = |x + 2| – 1
Solution:
Given that, f(x) = |x + 2| – 1
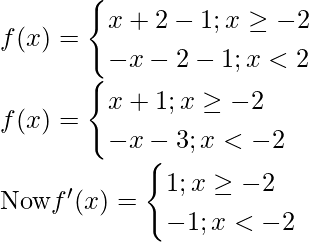
At x = -2 f'(x) change sign from negative to positive, hence by first derivative test, x = -2
is a point of local minima.
So, the minimum value f = f(-1)= |(-1)+ 2| – 1 = -1
So this function doesn’t contain maximum value
(ii) g(x) = -|x + 1| + 3
Solution:
Given that, g(x) = -|x + 1| + 3
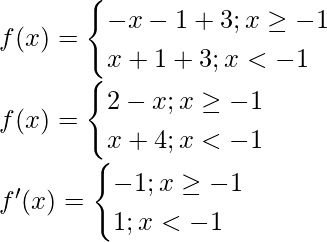
At x = -1 f'(x) change sign from positive to negative, hence by first derivative test, x = -1
is a point of local minima.
So, the maximum value of f = f(-1) = -|(-1) + 1| + 3 = 3
So, this function doesn’t contain minimum value
(iii) h(x) = sin 2x + 5
Solution:
Given that, h(x) = sin(2x) + 5
On differentiate both side w.r.t x, we get
h'(x) = 2cos2x
Now put h'(x) = 0
2cos 2x = 0
2x = (2x – 1)π/2
x = (2x – 1)π/4
Let’s perform second derivative test,
h”(x) = -4sin2x
h”(π/4) < 0
& so on.
So, 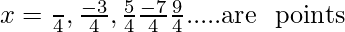
of local maxima.
& 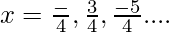 are points of local minima.
are points of local minima.
So, the minimum value of the given function is 4 and the maximum value of the given function is 6
(iv) f(x) = |sin(4x + 3)|
Solution:
Given that, f(x) = |sin(4x + 3)|
Now for any value of x, sin4x has the least value as -1. i.e., sin 4x + 3 ≥ 2
So f(x) = |sin(4x + 3)| = sin 4x + 3
On differentiate both side w.r.t x, we get
f'(x) = 4cos4x
Now put f'(x) = 0
4cos 4x = 0
4x = (2x – 1)π/2
x = (2x – 1)π/8
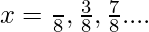 & son on
& son on
Let’s perform second derivative test,
f”(x) = -16 sin4x
f”(π/8) < 0; f”(3π/8) > 0; f”(5π/8) < 0
So,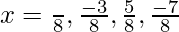 …. are points of local maxima. Minimum value = 4.
…. are points of local maxima. Minimum value = 4.
& 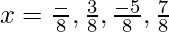 are points of local minima. Minimum value = 2.
are points of local minima. Minimum value = 2.
(v) h(x) = x + 1, x ∈ (-1, 1)
Solution:
Given that, h(x) = x + 1, x ∈ (-1, 1)
As we can clearly see from the function that h(x) is a strictly increasing function.
So, the minimum value of x will give minimum value of h(x).
Now, x ∈ (-1, 1)
So, this function has no minimum nor maximum value.
Question 3. Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum values, as the case may be:
(i) f(x) = x2
Solution:
Given that f(x) = x2
On differentiate both side w.r.t x, we get
f'(x) = 2x
Now put f'(x) = 0
2x = 0
x = 0
Let’s do second derivative test,
f”(x) = 2 > 0
At, x = 0, f'(x) = 0 and f”(x) > 0,
So x = 0 is a point of local minima. Local minimum value.
(ii) g(x) = x3 – 3x
Solution:
Given that g(x) = x3 – 3x
On differentiate both side w.r.t x, we get
g'(x) = 3x2 – 3
Now put g'(x) = 0
3x2 – 3 = 0
x2 = 1
x = ±1
Let’s do the second derivative test,
g”(x) = 6x ….(i)
g”(1) = 6 > 0
g”(-1) = -6 > 0
So by second derivatives test, x = 1 is a point of local maxima and the maximum value is
g(1) = (1)3 – 3(1) = -2
So by second derivatives test, x = -1 is a point of local minima and the minimum value is
g(-1) = (-1)3 – 3(-1) = 2
Hence, the local minimum value is -2 and the local maximum value is 2
(iii) h(x) = sin x + cos x, 0 < x < π/2
Solution:
h(x) = sin x + cos x, x∈(0,π/2)
On differentiate both side w.r.t x, we get
h'(x) = cos x – sin x
Now put h'(x) = 0
cos x – sin x = 0
cos x = sin x, x ∈ (0, π/2)
Clearly x = π/4 [both cos x and sin x attain 1/√2 at π/4]
Let’s do second derivative test,
h”(x) = -sin x – cos x
h”(π/4) = 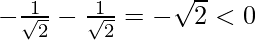
At 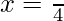 is a point of local maxima and the maximum value is
is a point of local maxima and the maximum value is
h(π/4) = sin π/4 + cos π/4
= 1/√2 + 1/√2 = √2
(iv) f(x) = sin x – cos x, 0 < x < 2π
Solution:
Given that, f(x) = sin x – cos x, x ∈ (0, 2π)
On differentiate both side w.r.t x, we get
f'(x) = cos x + sin x
Now put f'(x) = 0
cos x + sin x = 0
x = 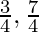 in (0, 2π)
in (0, 2π)
Now let’s do the second derivative test
f”(x) = -sin x + cos x
f”(3π/4) = – √2 > 0
f”(7π/4) = √2 > 0
So by second derivatives test, x = 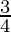 is a point of local maxima and the maximum value is
is a point of local maxima and the maximum value is
f(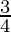 ) = -sin 3π/4 + cos 3π
) = -sin 3π/4 + cos 3π
4 = 1/√2 + 1/√2 = √2 > 0
So by second derivatives test, x = 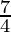 is a point of local minima and the minimum value is
is a point of local minima and the minimum value is
f(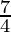 ) = -sin 7π/4 + cos 7π
) = -sin 7π/4 + cos 7π
4 = -1/√2 – 1/√2 = -√2 > 0
Hence, the local minimum value is -√2 and the local maximum value is √2.
(v) f(x) = x3 – 6x2 + 9x + 15
Solution:
Given that, f(x) = x3 – 6x2 + 9x + 15
On differentiate both side w.r.t x, we get
f'(x) = 3x2 – 12x + 9
Now put f'(x) = 0
3x2 – 12x + 9 = 0
3(x2 – 4x + 3) = 0
x = 1, 3
Let’s do the second derivative test,
f”(x) = 6x – 12
f”(1) = -6 < 0
f”(3) = 6 > 0
So by second derivatives test, x = 1 is a point of local maxima and the maximum value is
f'(1) = 3(1)2 – 12(1) + 9 = 19
So by second derivatives test, x = 3 is a point of local minima and the minimum value is
f'(3) = 3(3)2 – 12(3) + 9 = 15
Hence, the local minimum value is 15 and the local maximum value is 19.
(vi) 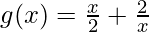 , x > 0
, x > 0
Solution:
Given that, 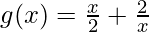 , x > 0
, x > 0
On differentiate both side w.r.t x, we get
g'(x)=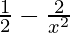
Now put g'(x) = 0
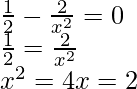 but ‘x > 0’
but ‘x > 0’
So, x = 2
Now we will do the second derivative test,
g”(x)=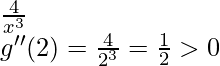
Hence, x = 2 is a point of local minima.
Local maximum value = g(2) = 2
(vii) 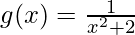
Solution:
Given that, 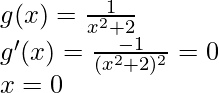
On differentiate both side w.r.t x, we get
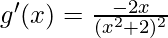
Now put g'(x) = 0
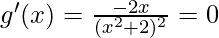
Now, let’s perform the second derivative test,
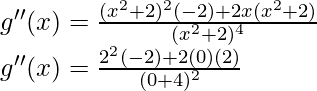
= -8/16 = -1/2 < 0
At x = 0, g'(x) = 0 and g”(x) < 0
Hence, ‘x = 0’ is a point of local maxima.
Now the domain of g(x) is (-∞, ∞).
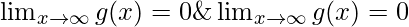
Value of g(x) at the extreme values of x is 0
So the global maxima of g(x)=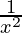 is at x = 0.
is at x = 0.
The maximum value is g(0) = 1/2
(viii) 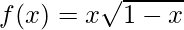 , x > 0
, x > 0
Solution:
Given that, 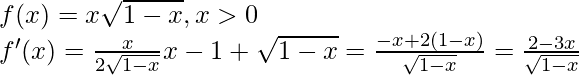
Now put f'(x) = 0
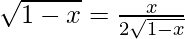
2(1 – x) = x
2 – 2x = x
3x = 2
x = 2/3
Now let’s do the second derivative test,
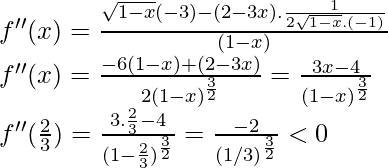
x = 2/3 is a point of local maxima f(2/3) = 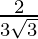
Now, f (x) = x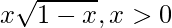
For domain, 1 – x ≥ 0 or x ≤ 1
So x ∈ [0, 1]
Local maxima is at x = 2/3 and the local maximum value is 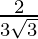
Question 4. Prove that the following function do not have maxima or minima:
(i) f(x) = ex
Solution:
Given that, f(x) = ex
f'(x) = ex
Now ex > 0, f'(x) > 0
Hence, f(x) is a strictly increasing function with no maxima or minima.
(ii) g(x) = log x
Solution:
Given that, g(x) = log x
g'(x) = 1/x
Now the domain of log x is x > 0
So, 1/x > 0, i.e., g'(x) > 0
Hence, g(x) is a strictly increasing function with no maxima or minima.
(iii) h(x) = x3 + x2 + x + 1
Solution:
Given that, h(x) = x3 + x2 + x + 1
h'(x) = 3x2 + 2x + 1
Now for this quadratic expression 3x2 + 2x + 1,
Its discriminant 0 = 22 – 4(3)(1) = -8 < 0
So, 3x2 + 2x + 1 > 0
Hence, h(x) is a strictly increasing function with no maxima or minima.
Question 5. Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals:
(i) f(x) = x3, x ∈ [-2, 2]
Solution:
Given that, f(x) = x3, x ∈ [-2, 2]
f'(x) = 3x2
f'(x) = 0 at x = 0
f”(x) = 6x
f”(0) = 0, second derivative failure
Now f'(3+) > 0 and f'(3–) > 0
f'(x) does not change sign at x = 0.
x = 0 is neither maxima nor minima
f(x) = x3 is a strictly increasing function.
(ii) f(x) = sin x + cos x, x ∈ [0, π]
Solution:
Given that, f(x) = sin x + cos x, x ∈ [0, π]
First derivative
f'(x) = cos x – sin x
Now put f'(x) = 0
cos x = sin x
x = π/4
On applying second derivative test,
f”(x) = -sin x – cos x
f”(π/4) = 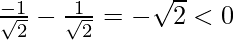
Hence, x = π/4 is pof local maxima . f(π/4)=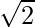
Now, for global maxima = max{f(0), f(π/4), f(π)}
= max{1, √2, -1}
For global maxima is at x = π/4 and the global maximum value is √2.
Now, for global minima = max{f(0), f(π/4), f(π)}
= max{1, √2, -1}
Global minima is at x = π and the global minimum value is -1.
(iii) ![Rendered by QuickLaTeX.com f(x)=4x-\frac{1}{2}x^2,x∈[-2,\frac{9}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-982b0eeef07a3b383e598d797a642e5a_l3.png)
Solution:
Given that, ![Rendered by QuickLaTeX.com f(x)=4x-\frac{1}{2}x^2,x∈[-2,\frac{9}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fbf68163e44ff1171e89ca8150883d2f_l3.png)
f'(x) = 4 – x
Now put f'(x) = 0
4 – x = 0
x = 4
Now applying second derivative test f”(x) = -1 < 0
Hence, x = 4 is a pt. of local maxima.
f(4) = 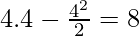
Global maxima = max{f(-2), f(4), f(9/2)}
= max{-10, 8, 7.8}
= 8
Global maxima occur at x = 9/2 and global maximum value is f(9/2) = 8
Global minima = min{f(-2), f(4), f(9/2)}
= max{-10, 8, 16.9}
= -10
Global minima occur at x = -2 and the global minimum value is f(-2) = -10.
(iv) f(x) = (x – 1)2 + 3, x ∈ [-3, 1]
Solution:
Given that, f(x) = (x – 1)2 + 3, x ∈ [-3, 1]
f'(x) = 2(x – 1)
Now put f'(x) = 0
2(x – 1) = 0
x = 1
Now applying second order derivative test,
f”(x) = 2 > 0
Hence, x = 1 is a point of local minima. f(1) = 3
Global maxima = max{f(-3), f(1)}
= max{19, 3}
= 19
The global or absolute maxima occurs at x = -3 and the absolute maximum value is f(-3) = 19
Global minima = min{f(-3), f(1)}
= min{19, 3]
= 3
The global or absolute minima occurs at x = 1 and the absolute value is f(1) = 3
Question 6. Find the maximum profit that a company can make, if the profit function is given by p(x) = 41 – 24x – 18x2
Solution:
Given that p(x) = 41 – 24x – 18x2
p'(x) = -24 – 36x
Now put p'(x) = 0
-24 – 36x = 0
x = -24/36
x = -2/3
Now, doing the second order derivative test,
p”(x) = -36 < 0
Hence, x = -2/3 is point of local maxima.
Now in quadratic function with domain R, if there is a local maxima, it is the global maxima also. BC3 p(-∞)⇢ -∞ and p(+∞)⇢ -∞
The maximum profit is p(-2/3) = 49
If negative units (x) do not exist, then maximum profit is p(0) = 41.
Question 7. Find both the maximum value and the minimum value of 3x4 – 8x3 + 12x2 – 48x + 25 on the interval [0, 3].
Solution:
Given that f(x) = 3x4 – 8x3 + 12x2 – 48x + 25, x ∈ [0, 3]
f'(x) = 12x2 – 24x2 + 24x – 48
Now put f'(x) = 0
12x3 – 24x2 + 24x – 48 = 0
12(x2 – 2x2 + 2x – 4) = 0
12(x2(x – 2) + 2(x – 2)) = 0
12(x2 + 2)(x – 2) = 0
x = 2 because x2 + 2 ≠ 0
Now applying second derivative test,
f”(x) = 12(3x2 – 4x + 2)
f”(2) = 12(3.22 – 4.2 + 2)
f”(2) = 12.6 = 72 > 0
Hence, x = 2 is point of local minima.
f(2) = -39
Global maxima = max{f(0), f(2), f(3)}
= max{25, -39, 16}
= 25
Global maxima occur at x = 0 and the global maximum is 25.
Global minima = min{f(0), f(2), f(3)}
= min{25, -39, 16}
= -39
Global minima occur at x = 2 andthe global minimum value is -39.
Question 8. At what points in the interval[0, 2π], does the function sin 2x attain its maximum value?
Solution:
Given that, f(x) = sin 2x , x ∈ [0, 2π]
f'(x) = 2 cos 2x
Now put f'(x) = 0
2cos2x = 0
2x = (2x – 1)π/2
x = (2x – 1)π/4
x = π/4, 3π/4, 5π/4, 7π/4
Now let’s do second order derivative test.
f”(x) = -4 sin2x
f”(π/4) = 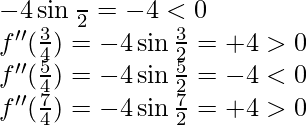
x = π/4 and x = 5π/4 are point of local maxima.
x = 3π/4 and x = 7π/4 are point of local minima.
f(π/4) = f(5π/4) = 1 and f(3π/4) = f(7π/4) = -1
Now,
Global maxima = max{f(0), f(π/4), f(3π/4), f{5π/4}, f(7π/4), f(2π)}
= max{0, 1, -1, 1, -1, 0}
= 1
Global maxima occur at the points x = π/4 and x = 5π/4 and the absolute maximum value is 1.
Question 9. What is the maximum value of the function sin x + cos x?
Solution:
Given that, f(x) = sin x + cos x
f'(x) = cos x – sin x
Now put f'(x) = 0
cos x = sin x
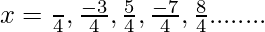
= {-√2, √2, +√2, -√2, -√2}
Now, second order derivative test,
f”(x) = -sin x – cos x
f”(π/4) = f”(9π/4) = f”(17π/4)……….. = -√2 < 0
A liter ⇢ f(x) = sin x + cos x = 
= 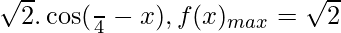
Question 10. Find the maximum value of 2x3 – 24x + 107 in the interval [1, 3]. Find the maximum value of the same function in [-3, -1].
Solution:
Given that f(x) = 2x3 – 24x + 107
On differentiating w.r.t. x we get
f'(x) = 6x2 – 24
Now, put f'(x) = 0
6x2 = 24
x2 = 4
x = ±2
Now second order test
f”(x) = 12x
f”(2) = 12.2 = 24 > 0
x = 2 is a pt. of local minima
f(2) = 75
f”(-2) = 12(-2) = -24 < 0
x = -2 is point of local maxima. f(-2) = 139
Now, in the interval [1, 3]
Global maxima = max{f(1), f(2), f(3)}
= max{85, 75, 89}
= 89
Now, in the interval [-3,-1]
Global maxima = max{f(-3), f(-2), f(-1)}
= max{125, 139, 129}
= 139
Question 11. It is given that at x = 1, the function x4 – 62x2 + ax + 9 attains its maximum value on the interval [0, 2]. Find the value of a.
Solution:
Give that, f(x) = x4 – 62x2 + ax + 9
On differentiating w.r.t. x we get
f'(x) = 4x3 – 124x + a
The maximum value is attained at x = 1, and 1 lies between 0 and 2.
So, at x = 1, there must be a local maxima
That means, f'(1) = 0
f'(1) = 4(1)3 – 124(1) + a = 0
-120 + a = 0
a = 120
Question 12. Find the maximum and minimum values of x + sin2x on [0, 2π].
Solution:
Give that f(x) = x + sin2x, x ∈ [0, 2π]
On differentiating w.r.t. x we get
f'(x) = 1 + 2cos2x
Now put f'(x) = 0, we get
1 + 2cos2x = 0
cos2x = -1/2
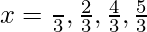 ∈ [0, 2π]
∈ [0, 2π]
Now,
For global maxima = max{f(0), f(π/3), f(4π/3), f(2π)}
= max{0, π/3, 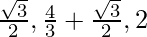 }
}
= 2π
Global maxima occur at x = 2π and the maximum value is f(2π) = 2π.
For global minima = min{f(0), f(2π/3), f(5π/3), f(2π)}
= min{0, 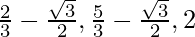 }
}
= 0
Global minima occur at x = 0 and the minimum value is 0.
Share your thoughts in the comments
Please Login to comment...