Class 12 NCERT Solutions- Mathematics Part I – Chapter 5 Continuity And Differentiability – Exercise 5.3
Last Updated :
09 Mar, 2021
Find  of the following:
of the following:
Question 1. 2x + 3y = sin x
Solution:
On differentiating both sides w.r.t. x, we get
2 + 3  = cos x
= cos x
3  = cos x – 2
= cos x – 2
 = (cosx – 2)/3
= (cosx – 2)/3
Question 2. 2x + 3y = sin y
Solution:
On differentiating both sides w.r.t. x, we get
2 + 3  = cos y
= cos y
(cosy – 3)  = 2
= 2
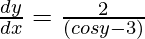
Question 3. ax + by2 = cos y
Solution:
On differentiating both sides w.r.t. x, we get
a + b * 2y( ) = -sin y *
) = -sin y * 
(2by + siny)  = -a
= -a
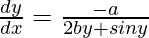
Question 4. xy + y2 = tan x + y
Solution:
On differentiating both sides w.r.t. x, we get
(x * + y) + 2y
+ y) + 2y = sec2x +
= sec2x + 
(x + 2y – 1) = sec2x – y
= sec2x – y
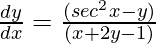
Question 5. x2 + xy + y2 = 100
Solution:
On differentiating both sides w.r.t. x, we get
2x + (x + y) + 2y
+ y) + 2y = 0
= 0
(x + 2y) *  = -(2x + y)
= -(2x + y)
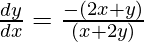
Question 6. x3 + x2y + xy2 + y3 = 81
Solution:
Differentiate both sides w.r.t. x
3x2+(x2 + y * 2x) + (x * 2y *
+ y * 2x) + (x * 2y *  + y2) + 3y2 *
+ y2) + 3y2 *  = 0
= 0
(x2 + 2xy + 3y2) = -(3x2 + 2xy + y2)
= -(3x2 + 2xy + y2)
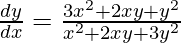
Question 7. Sin2y + cos xy = π
Solution:
Differentiate both sides w.r.t. x
2 sin y *  (siny) – sin(xy) *
(siny) – sin(xy) *  xy = 0
xy = 0
2sin y * cosy  – sin(xy)(x *
– sin(xy)(x *  + y) = 0
+ y) = 0
(2sin cos y – sin (xy) – x))  = y(xy)
= y(xy)
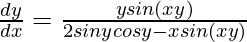
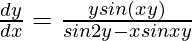
Question 8. sin2 x + cos2 y = 1
Solution:
2 sin x *  (sin x) + 2 cos y *
(sin x) + 2 cos y *  (cos y) = 0
(cos y) = 0
2 sin x * cos x + 2 cos y*(-sin y) *  = 0
= 0
2 sin x * cos x – 2 cos x – 2 cos y sin y *  = 0
= 0
Sin(2x) – sin(2y) –  = 0
= 0
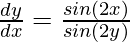
Question 9. y = sin-1(\frac{2x}{(1 + x2)}
Solution:
Put x = tanθ
θ = tan-1x
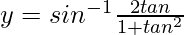
y = sin-1(sin 2θ)
y = 2θ
y = 2tan-1x -(1)
On differentiating eq(1), we get
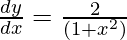
Question 10. 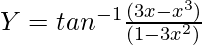 , -1/√3 < x < 1/√3
, -1/√3 < x < 1/√3
Solution:
Put x = tanθ
θ = tan-1x
y = 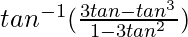
y = tan-1(tan 3θ)
y = 3θ
y = 3tan-1x -(1)
On differentiating eq(1), we get
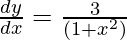
Question 11. 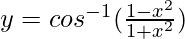 , 0 < x < 1
, 0 < x < 1
Solution:
Put x = tanθ
θ = tan-1 x
y = 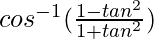
y = cos-1(cos 2θ)
y = 2θ
y = 2tan-1x -(1)
On differentiating eq(1), we get
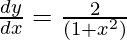
Question 12. 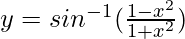 , 0 < x < 1
, 0 < x < 1
Solution:
Put x = tanθ
θ = tan-1x
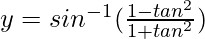
y = sin-1(cos 2θ)
y = sin-1(sin (π/2 – 2θ))
y = π/2 – 2θ
y = π/2 – 2 tan-1x
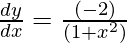
Question 13. 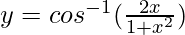 , -1 < x < 1
, -1 < x < 1
Solution:
Put x = tanθ
θ = tan-1x
y = cos^{-1}(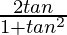 )
)
y = cos-1(sin 2θ)
y = cos-1(cos (π/2 – 2θ))
y = π/2 – 2θ
y = π/2 – 2tan-1x
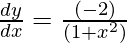
Question 14. 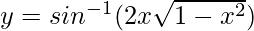 , -1/√2 < x < 1/√2
, -1/√2 < x < 1/√2
Solution:
Put x = sinθ
θ = sin-1 x
y = sin-1(2sinθ√(1 – sin2θ))
y = sin-1(sin 2θ) = 2θ
y = 2sin-1x
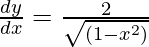
Question 15. 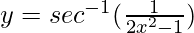 , 0 < x < 1/√2
, 0 < x < 1/√2
Solution:
Put x = tanθ
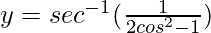
y = sec-1(1/cos2θ))
y = sec-1(sec2θ) = 2θ
y = 2cos-1x
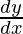 =
= 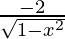
Share your thoughts in the comments
Please Login to comment...