Class 12 NCERT Solutions- Mathematics Part I – Chapter 3 Matrices – Miscellaneous Exercise on Chapter 3

Question 1: Let 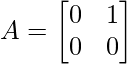, show that (aI + bA)ⁿ = aⁿ I + na^{n – 1} bA, where I is the identity matrix of order 2 and n ∈ N.

Solution:

Using mathematical induction,

Step 1: Let’s check for n=1

(aI + bA)ⁿ = (aI + bA)¹ = (aI + bA)

aⁿI + na^{n – 1} bA = aI + 1a^{1 – 1} bA = (aI + bA)

It is true for P(1)

Step 2: Now take n=k

(aI + bA)^k = a^kI + ka^{k – 1} bA …………………(1)

Step 3: Let’s check whether, its true for n = k+1

(aI + bA)^k+1 = (aI + bA)^k (aI + bA)

= (a^kI + ka^{k – 1} bA) (aI + bA)

= a^k+1I×I + ka^k bAI + a^k bAI + ka^k-1 b²AA

AA =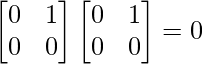 

= a^k+1I×I + ka^k bAI + a^k bAI + 0

= a^k+1I + (k+1)a^k+1-1 bA

= P(k+1)

Hence, P(n) is true.

Question 2: If 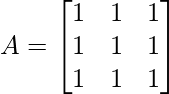, prove that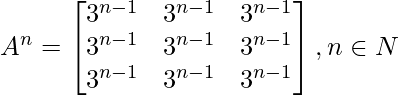 

Solution:

Using mathematical induction,

Step 1: Let’s check for n=1

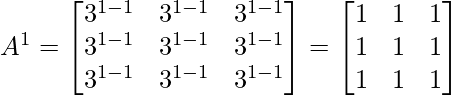
It is true for P(1)

Step 2: Now take n=k

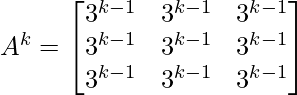
Step 3: Let’s check whether, its true for n = k+1

= P(k+1)

Hence, P(n) is true.

Question 3: If 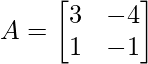, prove that  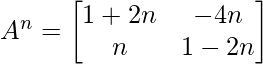,where n is any positive integer.

Solution:

Using mathematical induction,

Step 1: Let’s check for n=1

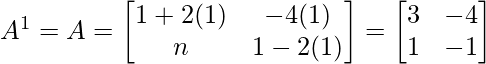
It is true for P(1)

Step 2: Now take n=k

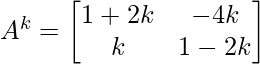
Step 3: Let’s check whether, its true for n = k+1

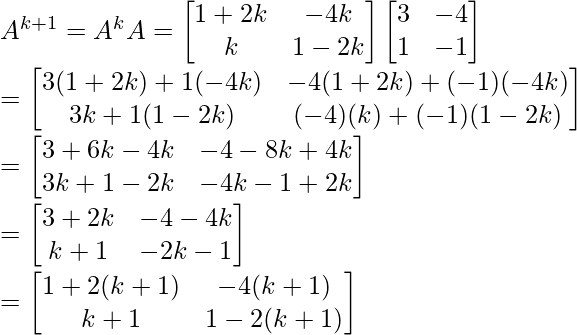
= P(k+1)

Hence, P(n) is true.

Question 4. If A and B are symmetric matrices, prove that AB – BA is a skew-symmetric matrix.

Solution:

As, it is mentioned that A and B are symmetric matrices,

A’ = A and B’ = B

(AB – BA)’ = (AB)’ – (BA)’  (using, (A-B)’ = A’ – B’)

= B’A’ – A’B’                     (using, (AB)’ = B’A’)

= BA – AB

(AB – BA)’ = – (AB – BA)

Hence, AB – BA is a skew symmetric matrix

Question 5. Show that the matrix B′AB is symmetric or skew-symmetric according as A is symmetric or skew-symmetric.

Solution:

Let’s take A as symmetric matrix

A’ = A

Then,

(B′AB)’ = {B'(AB)}’

= (AB)’ (B’)’            (using, (AB)’ = B’A’)

= B’A’ (B)              (using, (AB)’ = B’A’ and (B’)’ = B)

= B’A B

As, here (B′AB)’ = B’A B. It is a symmetric matrix.

Let’s take A as skew matrix

A’ = -A

Then,

(B′AB)’ = {B'(AB)}’

= (AB)’ (B’)’            (using, (AB)’ = B’A’)

= B’A’ (B)              (using, (AB)’ = B’A’ and (B’)’ = B)

= B'(-A) B

= – B’A B

As, here (B′AB)’ = -B’A B. It is a skew matrix.

Hence, we can conclude that B′AB is symmetric or skew symmetric according as A is symmetric or skew symmetric.

Question 6. Find the values of x, y, z if the matrix 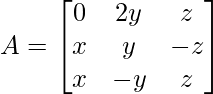 satisfy the equation A′A = I

Solution:

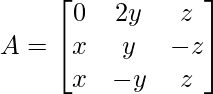
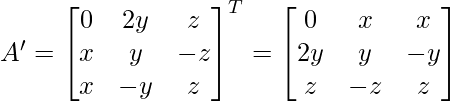
A’A =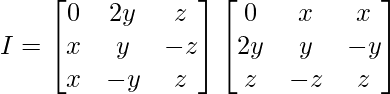 

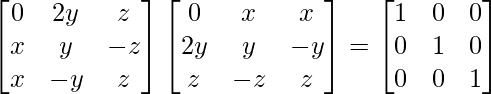
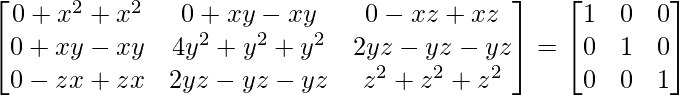
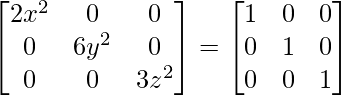
By evaluating the values, we have

2x² = 1

x = ±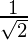 

6y² = 1

y = ±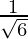 

3z² = 1

z = ±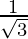 

Question 7: For what values of x : 

Solution:

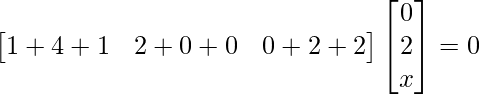
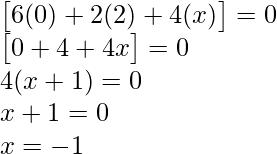
Question 8: If 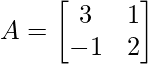, show that A² – 5A + 7I = 0.

Solution:

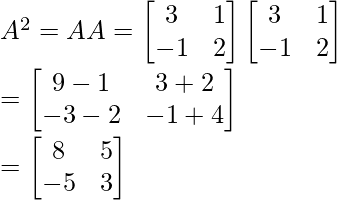
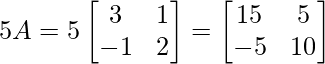
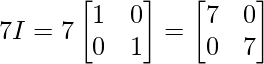
A² – 5A + 7I =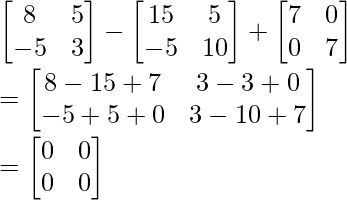 

Hence proved!

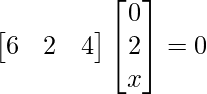
Question 9: Find x, if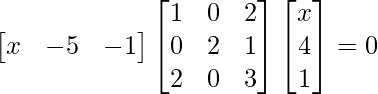 

Solution:

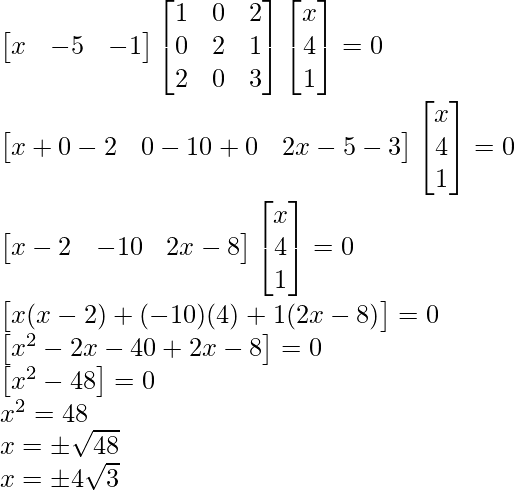
Question 10: A manufacturer produces three products x, y, z which he sells in two markets.

Annual sales are indicated below:

Market	Products
I	10,000	2,000	18,000
II	6,000	20,000	8,000

(a) If unit sale prices of x, y and z are ₹ 2.50, ₹ 1.50 and ₹ 1.00, respectively, find the total revenue in each market with the help of matrix algebra.

Solution:

Total revenue in market I and II can be arranged from given data as follows:

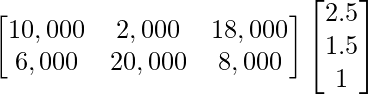
After multiplication, we get

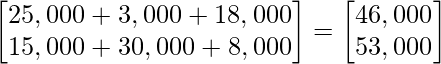
Hence, the total revenue in Market I and market II are ₹ 46,000 and ₹ 53,000 respectively.

(b) If the unit costs of the above three commodities are ₹ 2.00, ₹ 1.00 and 50 paise respectively. Find the gross profit.

Solution:

Total cost prices of all the products in market I and market II can be arranged from given data as follows:

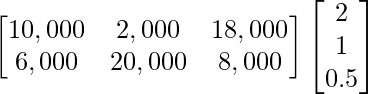
After multiplication, we get

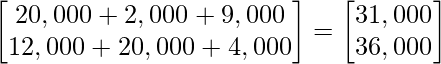
As, Profit earned = Total revenue – Cost price

Profit earned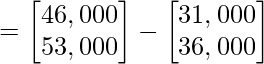 

Profit earned =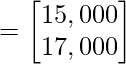 

Hence, profit earned in Market I and market II are ₹ 15,000 and ₹ 17,000 respectively. Which is equal to ₹ 32,000

Question 11. Find the matrix X so that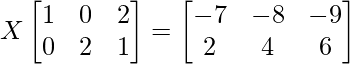 

Solution:

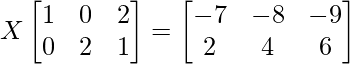
Here, the RHS is a 2×3 matrix and LHS is 2×3. So, X will be 2×2 matrix.

Let’s take X as,

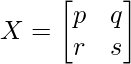
Now solving the matrix, we have

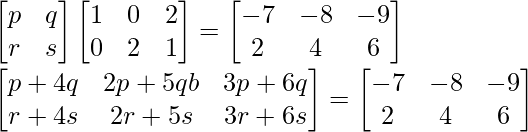
Equating each of them, we get

p+4q = -7 ………..(1)

2p+5q = -8 ………….(2)

3p + 6q = -9

r + 4s = 2 …………(3)

2r + 5s = 4 ……………(5)

3r + 6s = 6

Solving (1) and (2), we get

p = 1 and q = -2

Solving (3) and (4), we get

r = 2 and s = 0

Hence, matrix X is 

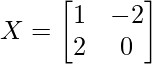
Question 12: If A and B are square matrices of the same order such that AB = BA, then prove by induction that ABⁿ = BⁿA. Further, prove that (AB)ⁿ = AⁿBⁿ for all n ∈ N.

Solution:

Using mathematical induction,

Step 1: Let’s check for n=1

ABⁿ = AB¹ = AB

BⁿA = B¹A = BA

It is true for P(1)

Step 2: Now take n=k

AB^k = B^kA

Step 3: Let’s check whether, its true for n = k+1

AB^(k+1) = AB^kB

= B^kAB

= B^k+1 A

= P(k+1)

Hence, P(n) is true.

Now, for (AB)ⁿ = AⁿBⁿ

Using mathematical induction,

Step 1: Let’s check for n=1

(AB)¹ = AB

B¹A¹ = BA

It is true for P(1)

Step 2: Now take n=k

(AB)^k = A^kB^k

Step 3: Let’s check whether, its true for n = k+1

(AB)^(k+1) = (AB)^k(AB)

= A^kB^k AB

= A^k+1 B^k+1

= (AB)^k+1

= P(k+1)

Hence, P(n) is true.

Choose the correct answer in the following questions: 

Question 13: If 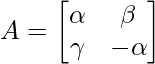 is such that A² = I, then

(A) 1 + α² + βγ = 0 

(B) 1 – α² + βγ = 0

(C) 1 – α² – βγ = 0 

(D) 1 + α² – βγ = 0

Solution:

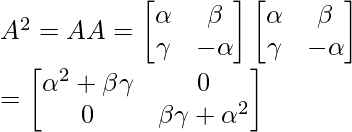
As, A² = I

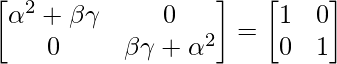
α² + βγ = 1

1 – α² – βγ = 0

Hence, Option (C) is correct.

Question 14. If the matrix A is both symmetric and skew symmetric, then

(A) A is a diagonal matrix 

(B) A is a zero matrix

(C) A is a square matrix 

(D) None of these

Solution:

If the matrix A is both symmetric and skew symmetric, then

A = A’

and A = -A

Only zero matrix satisfies both the conditions.

Hence, Option (B) is correct.

Question 15. If A is square matrix such that A² = A, then (I + A)³ – 7 A is equal to

(A) A 

(B) I – A 

(C) I 

(D) 3A

Solution:

(I + A)³ – 7 A = I³ + A³ + 3A^2 + 3AI^2 – 7A

= I3 + A3 + 3A² + 3A – 7A

= I + A³ + 3A² – 4A

As, A² = A

A3 = A²A = AA = A

So, I + A3 + 3A2 – 4A = I + A + 3A – 4A = I

Hence, Option (C) is correct.