Class 12 NCERT Solutions – Mathematics Part I – Chapter 4 Determinants – Exercise 4.4
Last Updated :
03 Apr, 2024
Find adjoint of each of the matrices in Exercises 1 and 2.
Question 1. 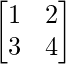
Solution:
A = 
A11 = 4; A12 = -3; A21 = -2; A22 = 1
adj A = 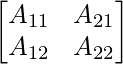
adj A = 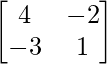
Question 2. 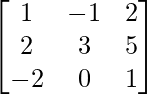
Solution:
A = 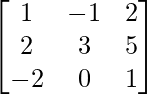
A11 = 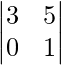
A11 = 3 – 0 = 3
A12 = 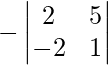
A12 = -(2 + 10) = -12
A13 = 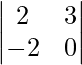
A13 = 0 + 6 = 6
A21 = 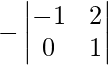
A21 = -(-1 – 0) = 1
A22 = 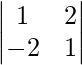
A22 = 1 + 4 = 5
A23 = 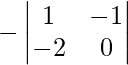
A23 = -(0 – 2) = 2
A31 = 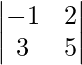
A31 = -5 – 6 = -11
A32 = 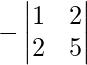
A32 = -(5 – 4) = -1
A33 = 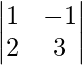
A33 = 3 + 2 = 5
adj A = 
adj A = 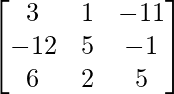
Verify A(adj A) = (adj A)A = |A| I in exercises 3 and 4.
Question 3. 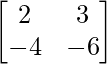
Solution:
|A| = -12 -(-12)
|A| = -12 + 12 = 0
so, |A|*I = 0 * 
|A|*I = ……… (1)
……… (1)
Now, for adjoint of A
A11 = -6
A12 = 4
A21 = -3
A22 = 2
adj A = 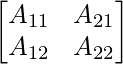
adj A = 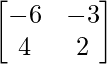
Now, A(adj A) = 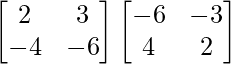
A(adj A) = 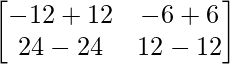 [Tex]\begin{bmatrix} 11& 0 &0 \\ 0 & 11 &0 \\ 0 & 0 & 11 \end{bmatrix}[/Tex]
[Tex]\begin{bmatrix} 11& 0 &0 \\ 0 & 11 &0 \\ 0 & 0 & 11 \end{bmatrix}[/Tex]
A(adj A) =  …………(2)
…………(2)
Now, (adj A)A = 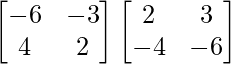
(adj A)A = 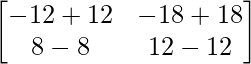
(adj A)A =  …………….(3)
…………….(3)
From eq(1), (2), and (3), you can see that A(adj A) = (adj A)A = |A|I
Question 4. 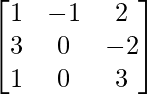
Solution:
A = 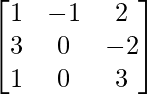
|A| = 1(0 – 0) + 1(9 + 2) + 2(0 – 0)
|A| = 11
|A| * I = 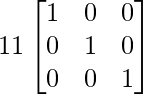
|A| * I = 
Now, for adjoint of A
A11 = 0
A12 = -(9 + 2) = -11
A13 = 0
A21 = -(-3 – 0) = 3
A22 = 3 – 2 = 1
A23 = -(0 + 1) = -1
A31 = 2 – 0 = 2
A32 = -(-2 – 6) = 8
A33 = 0 + 3 = 3
adj A = 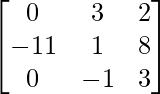
Now,
A(adjA) = 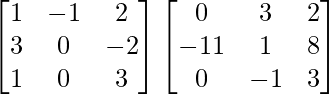
A(adj A) = 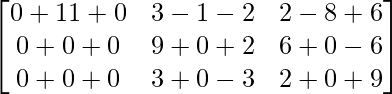
A(adj A) = 
Also,
(adj A).A = 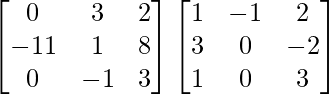
(adj A).A = 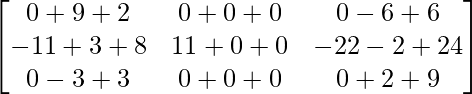
(adj A).A = 
From above, you can see,
A(adj A) = (adj A)A = I
Find the inverse of each of the matrices (if it exists) given in Exercises 5 to 11.
Question 5. 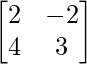
Solution:
|A| = 6 – (-8) = 14
|A| ≠ 0, So inverse exists.
A11 = 3
A12 = 2
A21 = -4
A22 = 2
adj A = 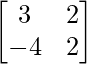
A-1 = (adj A)/|A|
A-1 = 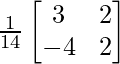
Question 6. 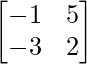
Solution:
A = 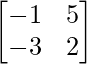
|A| = -2 + 15 = 13 ≠ 0
Hence, inverse exists.
A11 = 2
A12 = 3
A21 = -5
A22 = -1
adj A = 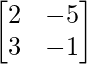
A-1 = (adj A)/|A|
A-1 = 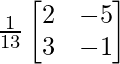
Question 7. 
Solution:
A = 
|A| = 1(10 – 0) – 2(0 – 0) + 3(0 – 0) = 10
For adj A
A11 = 10 – 0 = 0
A12 = -(0 – 0) = 0
A13 = 0 – 0 = 0
A21 = -(10 – 0) = -10
A22 = 5 – 0 = 5
A23 = -(0 – 0) = 0
A31 = 8 – 6 = 2
A32 = -(4 – 0) = -4
A33 = 2 – 0 = 2
adj A = 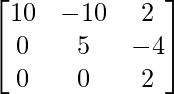
A-1 = (adj A)/|A|
A-1 = 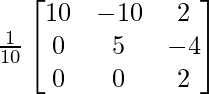
Question 8. 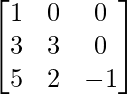
Solution:
A = 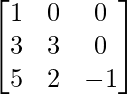
|A| = 1(-3 – 0) – 0 + 0 = -3 ≠ 0
Hence, inverse exists.
For adj A
A11 = -3 – 0 = -3
A12 = -(-3 – 0) = 3
A13 = 6 – 15 = -9
A21 = -(0 – 0) = 0
A22 = -1 – 0 = -1
A23 = -(2 – 0) = -2
A31 = 0 – 0 = 0
A32 = -(0 – 0) = 0
A33 = 3 – 0 = 3
adj A = 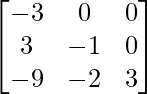
A-1 = (adj A)/|A|
A-1 = 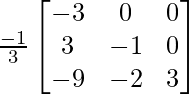
Question 9. 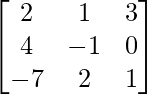
Solution:
A = 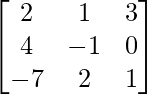
|A| = 2(-1 – 0) – 1(4 – 0) + 3(8 – 7) = -3 ≠ 0
Hence, inverse exists.
For adj A
A11 = -1 – 0 = -1
A12 = -(4 – 0) = -4
A13 = 8 – 7 = 1
A21 = -(1 – 6) = 5
A22 = 2 + 21 = 23
A23 = -(4 + 7) = -11
A31 = 0 + 3 = 3
A32 = -(0 – 12) = 12
A33 = -2 – 4 = -6
adj A = 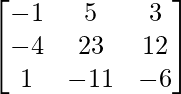
A-1 = (adj A)/|A|
A-1 = 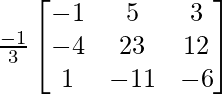
Question 10. 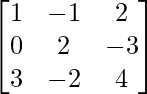
Solution:
A = 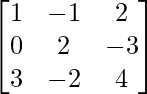
|A| = 1(8 – 6) – 0 + 3(3 – 4) = -1
Now for adj A
A11 = 8 – 6 =2
A12 = -(0 + 9) = -9
A13 = 0 – 6 = -6
A21 = -(-4 + 4) =0
A22 = 4 – 6 = -2
A23 = -(-2 + 3) = -1
A31 = 3 – 4 = -1
A32 = -(-3 – 0) = 3
A33 = 2 – 0 = 2
adj A = 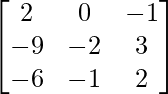
A-1 = (adj A)/|A|
A-1 = 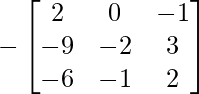
A-1 = 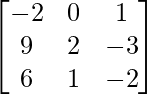
Question 11. 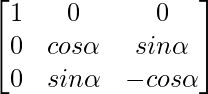
Solution:
A = 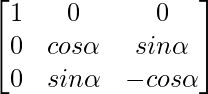
|A| = 1(-cos2α – sin2α) = -1
Now,
A11 = -cos2α – sin2α = -1
A12 = 0
A13 = 0
A21 = 0
A22 = -cosα
A23 = -sinα
A31 = 0
A32 = -sinα
A33 = cosα
adj A = 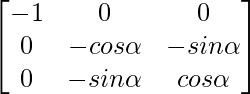
A-1 = (adj A)/|A|
A-1 = 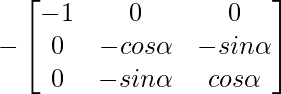
A-1 = 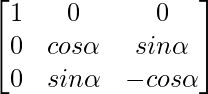
Question 12. Let A = 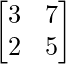 and B =
and B = 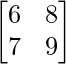 , verify that (AB) – 1 = B – 1A – 1
, verify that (AB) – 1 = B – 1A – 1
Solution:
A = 
|A| = 15 – 14 = 1
A11 = 5
A12 = -2
A21 = -7
A22 = 3
A-1 = (adj A)/|A|
A-1 = 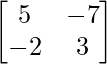
B = 
|B| = 54 – 56 = -2
adj B = 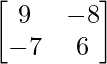
B-1 = (adj B)/|B|
B-1 = 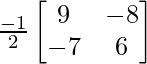
B-1 = 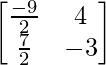
Now,
B-1A-1 = 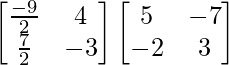
B-1A-1 = 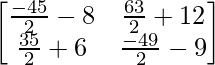
B-1A-1 = 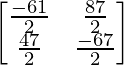
Now, AB = 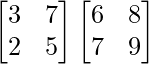
AB = 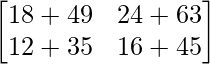
AB = 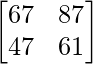
|AB| = 67 * 61 – 87 * 47 = -2
adj (AB) = 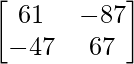
(AB)-1 = (adj AB)/|AB|
(AB)-1 = 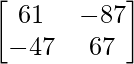
(AB)-1= 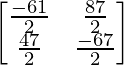
From above, you can see that (AB)-1 = B-1A-1.
Hence, it is proved.
Question 13. A = 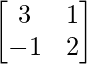 , show that A2 – 5A + 7I = O. Hence find A-1.
, show that A2 – 5A + 7I = O. Hence find A-1.
Solution:
A = 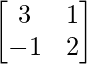
A2 = 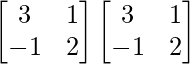
A2 = 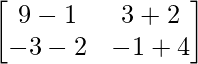
A2 = 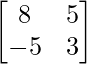
So, A2 – 5A + 7I
= 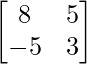 – 5
– 5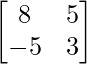 + 7
+ 7
= 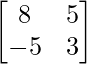 –
– 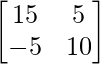 +
+ 
= 
= O
Hence, A2 – 5A + 7I = O
It can be written as
A.A – 5A = -7I
Multiplying by A-1 in both sides
A.A(A-1) – 5AA-1 = 7IA-1
A(AA-1) – 5I = -7A-1
AI – 5I = -7A-1
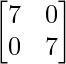
A-1 = -(A – 5I)/7
A-1 =1/7(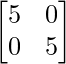 –
– 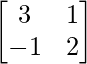 )
)
A-1 = 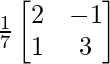
Question 14. For the matrix A =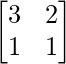 , find the numbers a and b such that A2 + aA + bI = O.
, find the numbers a and b such that A2 + aA + bI = O.
Solution:
A = 
A2 = 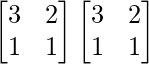
A2 = 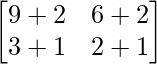
A2 = 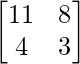
Now,
A2 – aA + bI = O
Multiplying by A-1 in both sides
(AA)A-1 + aAA-1 + bIA-1 = O
A(AA-1) + aI + b(IA-1) = O
AI + aI + bA-1 = O
A + aI = -bA-1
A-1 = -(A + aI)/b
Now,
A-1 = (adj A)/|A|
A-1 = 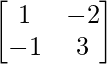
Now,
![Rendered by QuickLaTeX.com \begin{bmatrix} 1 &-2 \\ -1& 3 \end{bmatrix} = -1/b[\begin{bmatrix} 3 &2 \\ 1& 1 \end{bmatrix} + \begin{bmatrix} a &0 \\ 0& a \end{bmatrix}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-78d7045dbf4047f4d70a97e32e8789ef_l3.png)
= -1/b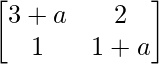
= 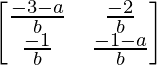
On comparing elements you will get
-1/b = -1
b = 1
(-3 – a)/b = 1
-3 – a = 1
a = -4
Hence, a = -4 and b = 1
Question 15. A = 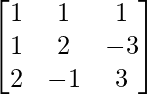 , show that A3 – 6A2 + 5A + 11I = O. Hence find A-1
, show that A3 – 6A2 + 5A + 11I = O. Hence find A-1
Solution:
A = 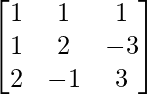
A2 = 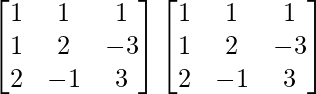
A2 = 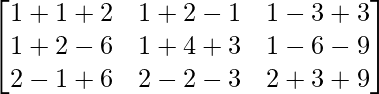
A2 = 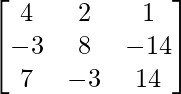
A3 = A2.A
A3 = 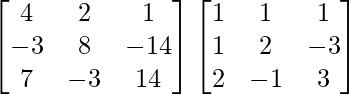
A3 = 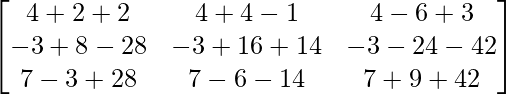
A3 = 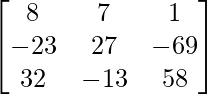
A3 – 6A2 + 5A + 11I
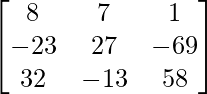 – 6
– 6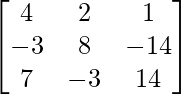 + 5
+ 5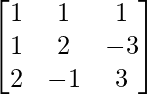 + 11
+ 11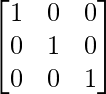
= 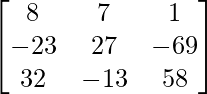 –
– 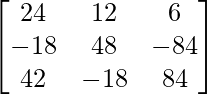 +
+ 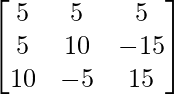 +
+ 
= 
= O
Hence, A3 – 6A2 + 5A + 11I = O
Now,
A3 – 6A2 + 5A + 11I = O
(AAA)A-1 – 6(AA)A-1 + 5(AA-1) + 11IA-1 = O
AA(AA-1) – 6A(AA-1) + 5(AA-1) = -11(IA-1)
A2 – 6A + 5I = -11 A-1
A-1 = -1/11(A2 – 6A + 5I) ………….(1)
Now, A2 – 6A + 5I
=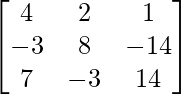 – 6
– 6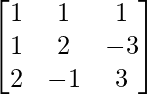 + 5
+ 5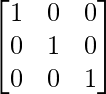
=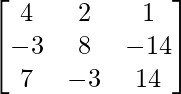 –
– 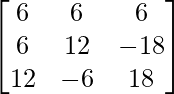 +
+ 
= 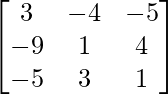
From eq(1) you have
A-1 = -1/11 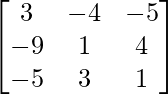
Question 16. A = 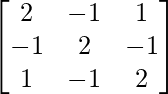 , verify that A3 – 6A2 + 9A – 4I = O and hence fin A-1.
, verify that A3 – 6A2 + 9A – 4I = O and hence fin A-1.
Solution:
A = 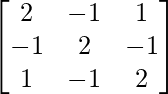
A2 = 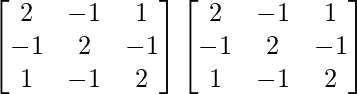
A2 = 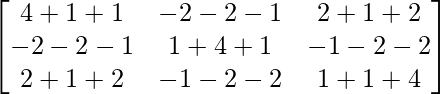
A2= 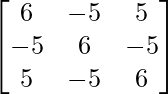
A3 = A2.A
A3 = 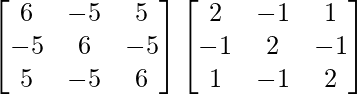
A3 = 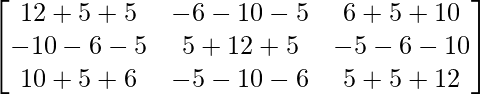
A3 = 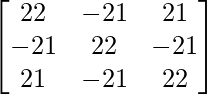
Now,
A3 – 6A2 + 9A – 4I
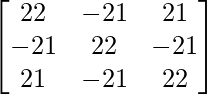 – 6
– 6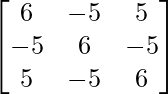 + 9
+ 9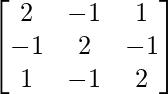 – 4
– 4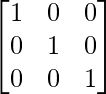
=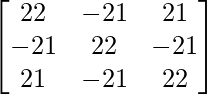 –
– 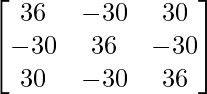 +
+ 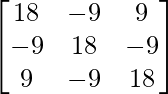 –
– 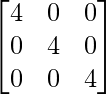
=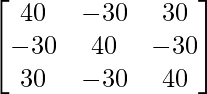 –
– 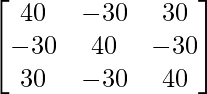
= 
= O
So, A3 – 6A2 + 9A – 4I = O
Now,
A3 – 6A2 + 9A – 4I = O
Multiplying by A-1 in both sides
(AAA)A-1 – 6(AA)A-1 + 9AA-1 – 4IA-1 = O
AA(AA-1) – 6A(AA-1) + 9(AA-1) = 4(IA-1)
AAI – 6AI +9I = 4A-1
A2 – 6A + 9I = 4A-1
A-1 = 1/4(A2 – 6A + 9I) ……….(1)
A2 – 6A + 9I
= 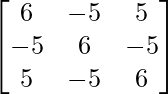 – 6
– 6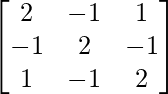 + 9
+ 9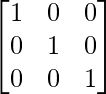
= 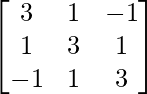
From eq(1), you have
A-1 = 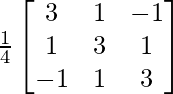
Question 17. Let A be a non-singular matrix of order 3 * 3. Then |adj A| is equal to
(A) |A| (B) |A|2 (C) |A|3 (D) 3|A|
Solution:
You know,
(adj A)A = |A|I
(adj A)A = 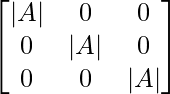
|(adj A)A| = 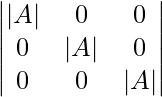
|(adj A)A| = |A|3
|(adj A)A| = |A|3 I
|adj A| = |A|3
Hence, option B is correct.
Question 18. If A is an invertible matrix of order 2, then det(A-1) is equal to
(A) det(A) (B) 1/(det A) (C) 1 (D) 0
Solution:
Since A is an invertible matrix then A-1 exists.
And A-1 = (adj A)/|A|
Suppose a 2 order matrix is A = 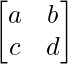
Then |A| = ad – bc
and adj A = 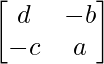
A-1 = (adj A)/|A|
A-1 = 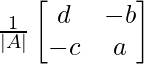
A-1 = 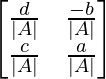
|A-1| = 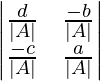
|A-1| = 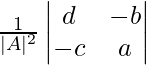
|A-1| = (ad – bc)/|A|2
|A-1| = |A|/|A|2
|A-1| = 1/|A|
det(A-1) = 1/(det A)
Hence, option B is correct.
Share your thoughts in the comments
Please Login to comment...