Content of this article has been merged with Chapter 1 Relations And Functions – Miscellaneous Exercise as per the revised syllabus of NCERT.
Question 11: Let S = {a, b, c} and T = {1, 2, 3}. Find F–1 of the following functions F from S to T, if it exists.
(i) F = {(a, 3), (b, 2), (c, 1)}
Solution:
As, F = {(a, 3), (b, 2), (c, 1)} and S = {a,b,c} and T={1,2,3}
F: S→T is defined as
F(a) = 3, F(b) = 2 and F(c) = 1
F is one-one and onto.
Taking F-1, so F-1: T→S
a = F-1(3), b = F-1(2) and c = F-1(1)
F-1 = {(3,a),(2,b),(1,c)}
(ii) F = {(a, 2), (b, 1), (c, 1)}
Solution:
As, F = {(a, 2), (b, 1), (c, 1)}
F: S→T is defined as
F(a) = 2, F(b) = 1 and F(c) = 1
Here, F(b) = F(c) but b ≠ c
Hence, F is not one-one.
So, F is not invertible and F-1 doesn’t exists.
Question 12. Consider the binary operations ∗ : R × R → R and o : R × R → R defined as a ∗b = |a – b| and a o b = a, ∀ a, b ∈ R. Show that ∗ is commutative but not associative, o is associative but not commutative. Further, show that ∀ a, b, c ∈ R, a ∗ (b o c) = (a ∗ b) o (a ∗ c). [If it is so, we say that the operation ∗ distributes over the operation o]. Does o distribute over ∗? Justify your answer.
Solution:
Binary operations ∗ : R × R → R defined as a ∗b = |a – b|
a*b = |a-b|
b*a = |b-a| = |-(a-b)| = |a-b|
a*b = b*a
Hence, ∗ is commutative.
Now, let’s take a=1, b=2 and c=3 for better understanding
a*(b*c) = a*|b-c| = |a-|b-c|| = |1-|2-3|| = 0
(a*b)*c = |a-b|*c = ||a-b|-c| = ||1-2|-3| = 2
a*(b*c) ≠ (a*b)*c
Hence, ∗ is not associative.
Binary operations o : R × R → R defined as a o b = a, ∀ a, b ∈ R
a o b = a
b o a = b
a o b ≠ b o a
Hence, o is not commutative.
a o (b o c) = a o b = a
(a o b) o c = a o c = a
a o (b o c) ≠ (a o b) o c
Hence, o is associative.
Let’s check for a ∗ (b o c) = (a ∗ b) o (a ∗ c) a, b, c ∈ R
a ∗ (b o c) = a * b = |a-b|
(a ∗ b) o (a ∗ c) = |a-b| o |a-c| = |a-b|
Hence, a ∗ (b o c) = (a ∗ b) o (a ∗ c)
Now, let’s check for a o (b * c) = (a o b) * (a o c)
a o (b * c) = a
(a o b) * (a o c) = a * a = |a-a| = 0
Hence, a o (b * c) ≠ (a o b) * (a o c)
o does not distribute over ∗
Question 13. Given a non-empty set X, let ∗ : P(X) × P(X) → P(X) be defined as A * B = (A – B) ∪ (B – A), ∀ A, B ∈ P(X). Show that the empty set φ is the identity for the operation ∗ and all the elements A of P(X) are invertible with A–1 = A.
(Hint : (A – φ) ∪ (φ – A) = A and (A – A) ∪ (A – A) = A ∗ A = φ).
Solution:
Set X, such that P(X) × P(X) → P(X) be defined as A * B = (A – B) ∪ (B – A), ∀ A, B ∈ P(X)
φ*A = (φ-A) U (A-φ) = φ U A = A
A*φ = (A-φ) U (φ-A) = A U φ = A
Hence, φ is the identity element for the operation * on P(X)
A*A = (A-A) U (A-A) = φ U φ = φ
⇒ A = A-1
Hence, all the elements A of P(X) are invertible with A–1 = A.
Question 14. Define a binary operation ∗ on the set {0, 1, 2, 3, 4, 5} as
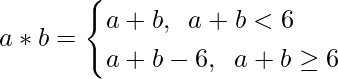
Show that zero is the identity for this operation and each element a ≠ 0 of the set is invertible with 6 – a being the inverse of a.
Solution:
Let the set x = {0, 1, 2, 3, 4, 5}
Let’s take i as identity element, where a*i = a = i*a ∀ a ∈ x
a*0 = a
0*a = a, when (a+0<6)
Hence, zero is the identity for this operation
An element a ∈ x is invertible if there exists b ∈ x such that a*b = b*a = 0
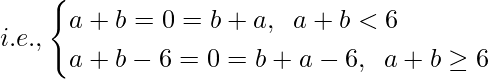
From above equations, we have
a = -b or b = 6-a
But, as x = {0, 1, 2, 3, 4, 5} and a,b∈ x. Then a≠-b
Hence, b = 6-a is the inverse of an element a∈ x
a≠0
a-1 = 6-a
Question 15. Let A = {– 1, 0, 1, 2}, B = {– 4, – 2, 0, 2} and f, g : A → B be functions defined by f(x) = x2 – x, x ∈ A and 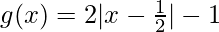 x ∈ A. Are f and g equal? Justify your answer.
x ∈ A. Are f and g equal? Justify your answer.
(Hint: One may note that two functions f : A → B and g : A → B such that f(a) = g (a) ∀ a ∈ A, are called equal functions).
Solution:
Given, f, g : A → B be functions defined by f(x) = x2 – x, x ∈ A and g(x) = 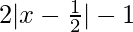 x ∈ A
x ∈ A
At x = -1
f(0) = (-1)2 – (-1) = 2
g(0) = 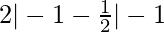 = 2
= 2
Here, f(-1) = g(-1) and 2=2
At x = 0
f(0) = 02 – 0 = 0
g(0) = 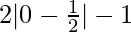 = 0
= 0
Here, f(0) = g(0) and 0=0
At x = 1
f(1) = 12 – 1 = 0
g(1) = 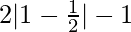 = 0
= 0
Here, f(1) = g(1) and 1=1
At x = 2
f(1) = 22 – 2 = 2
g(1) = 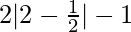 = 2
= 2
Here, f(2) = g(2) and 2=2
For, every c∈ A, f(c) = g(c)
Hence, f and g are equal functions.
Question 16. Let A = {1, 2, 3}. Then number of relations containing (1, 2) and (1, 3) which are reflexive and symmetric but not transitive is
(A) 1
(B) 2
(C) 3
(D) 4
Solution:
R = {(1,1),(1,2),(1,3),(2,1),(2,2),(3,1),(3,3)}
Reflexive : (1,1), (2,2), (3,3) ∈ R
Symmetric: (1,2), (2,1)∈ R and (1,3), (3,1) ∈ R
R is not Transitive because, (1,2), (1,3) ∈ R but (3,2) ∉R
So, if we will add (3,2) and (2,3) or both, then R will become transitive.
New, R = {(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)}
Hence, A is the correct option.
Question 17. Let A = {1, 2, 3}. Then number of equivalence relations containing (1, 2) is
(A) 1
(B) 2
(C) 3
(D) 4
Solution:
Smallest equivalence relations containing (1, 2):
R = {(1,1),(2,2),(1,2),(2,1),(3,3)}
or R = {(1,1),(2,2),(1,2),(2,1),(3,2),(2,3)(3,3)}
Hence, B is the correct option.
Question 18. Let f : R → R be the Signum Function defined as
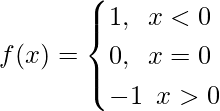
and g : R → R be the Greatest Integer Function given by g (x) = [x], where [x] is greatest integer less than or equal to x. Then, does fog and gof coincide in (0, 1]?
Solution:
Given, f : R → R and g : R → R
when x ∈ (0,1]
[x] = 1, when x=1
[x] = 0, when 0<x<1
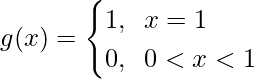
Now, fog(x)=f(g(x)) = f([x])
![Rendered by QuickLaTeX.com f([x])= \begin{cases} f(1), \hspace{0.2cm}x=1\\ f(0),\hspace{0.2cm}0<x<1 \end{cases} =](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-22a797a413258f8cb8d32f0ec62cc5d8_l3.png)
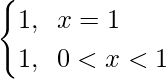
And, Now gof(x) = g(f(x))
g(1) = [1] = 1
g(0) = [0] = 0
g(-1) = [-1] = -1
When x ∈ (0,1), fog = 0 and gof = 1. fog(1) ≠ gof(1)
Hence, fog and gof do not coincide in (0, 1].
Question 19. Number of binary operations on the set {a, b} are
(A) 10
(B) 16
(C) 20
(D ) 8
Solution:
Let A = {a,b}
A x A = {a,b} x {a,b}
R = {(a,a),(a,b),(b,a),(b,b)}
Number of elements are 4.
Hence, the number of binary operations on the set will be 24 = 16
Hence, B is the correct option.
Share your thoughts in the comments
Please Login to comment...