Class 12 NCERT Solutions- Mathematics Part I – Application of Derivatives – Exercise 6.2| Set 2
Last Updated :
04 Apr, 2024
Content of this article has been merged with Chapter 5: Continuity and Differentiability – Exercise 6.2 as per the revised syllabus of NCERT.
Question 11. Prove that the function f given by f(x) = x2 – x + 1 is neither strictly increasing nor decreasing on (– 1, 1).
Solution:
Given: f(x) = x2 – x + 1
f'(x) = 2x – 1
For strictly increasing, f'(x) > 0
2x – 1 > 0
x > 1/2
So, f(x) function is increasing for x > 1/2 in the interval (1/2, 1) -(Given interval is (-1, 1)
Similarly, for decreasing f'(x) < 0
2x – 1 < 0
x < 1/2
So, f(x) function is increasing for x < 1/2 in the interval (-1, 1/2) -(Given interval is (-1, 1)
Hence, the function f(x) = x2 – x + 1 is neither strictly increasing nor decreasing.
Question 12. Which of the following functions are decreasing on (0, π/2).
(A) cos x (B) cos 2x (C) cos 3x (D) tan x
Solution:
(A) f(x) = cos x
f'(x) = -sin x
Now in (0, π/2) interval, sin x is positive(because it is second quadrant)
So, -sin x < 0
∴ f'(x) < 0
f(x) = cos x is strictly decreasing on(0, π/2).
(B) f(x) = cos 2x
f'(x) = -2 sin 2x
Now in (0, π/2) interval, sin x is positive(because it is second quadrant)
-sin 2x < 0
∴ f'(x) < 0,
f(x) = cos 2x is strictly decreasing on(0, π/2).
(C) f(x) = cos 3x
f'(x) = -3sin 3x
Let 3x = t
So in sin 3x = sin t
When t ∈(0, π), sin t + >0 or 3x ∈ (0, π)
But when π/3 < x < π/2
π < 3x < 3π/2
Here sin 3x < 0
So, in x ∈ (0, π/3),
f'(x) = -3sin 3x < 0 & in x∈(π/3, π/2), f'(x) = -3sin 3x > 0
f'(x) is changing signs, hence f(x) is not strictly decreasing.
(D) f(x) = tan x
f'(x) = sec2x
Now in x ∈ (0, π/2), sec2x > 0
Hence, f(x) is strictly increasing on(0, π/2).
So, option (A) and (B) are decreasing on (0, π/2).
Question 13. On which of the following intervals is the function f given by f(x) = x100 + sin x – 1 decreasing ?
(A) (0, 1) (B) π/2, π (C) 0, π/2 (D) None of these
Solution:
f(x) = x100 + sin x – 1
f'(x) = 100x99 + cos x
(A) In (0, 1) interval, x > 0, so 100x99 > 0
and for cos x: (0, 1°) = (0, 0.57°) > 0
Hence, f(x)is strictly increasing in interval(0, 1)
(B) In (π/2, π) interval,
For 100x99: x ∈ (π/2, π) = (11/7, 22/7) = (1.5, 3.1) > 1
So, x99 > 1. Hence 100x99 > 100
For Cos x: (π/2, π) in second quadrant and in second quadrant cos x is negative, so the value is in be -1 and 0.
Hence, f(x)is strictly increasing in interval (π/2, π)
(C) In (0, π/2) interval, both cos x > 0 and 100x99 > 0
So f'(x) > 0
Hence, f(x)is strictly increasing in interval (0, π/2)
So, the correct option is (D).
Question 14. For what values of a the function f given by f(x) = x2 + ax + 1 is increasing on (1, 2)?
Solution:
Given: f(x) = x2 + ax + 1
f'(x) = 2x + a
Now, x ∈ (1, 2), 2x ∈ (2, 4)
2x + a ∈ (2 + a, 4 + a)
For f(x) to be strictly increasing, f'(x) > 0
If the minimum value of f'(x) > 0 then
f'(x) on its entire domain will be > 0.
f'(x)min > 0
2 + a > 0
a > -2
Question 15. Let I be any interval disjoint from [–1, 1]. Prove that the function f given by 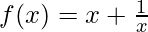 is increasing on I.
is increasing on I.
Solution:
Clearly the maximum interval I is R-(-1,1)
Now, f(x) = 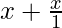
f'(x) = 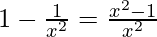
It is given that I be any interval disjoint from [–1, 1]
So, for every x ∈ I either x < -1 or x > 1
So, for x < -1, f'(x) is positive.
So, for x < 1, f'(x) is positive.
Hence, f'(x) > 0 ∀ x ∈ I, so, f(x) is strictly increasing on I.
Question 16. Prove that the function f given by f(x) = log sin x is increasing on (0, π/2) and decreasing on (π/2, π).
Solution:
f(x) = log sin x
f'(x) = 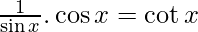
Interval (0, π/2), it is first quadrant, here cot x is positive.
So, f'(x) = cot x is positive (i.e., cot x > 0)
Hence, f(x) is strictly increasing in interval (0, π/2)
Interval (π/2, π), it is second quadrant, here cot x is negative.
So, f'(x) = cot x is negative (i.e., cot x < 0)
Hence, f(x) is strictly decreasing in interval (π/2, π)
Question 17. Prove that the function f given by f(x) = log|cos x| is decreasing on (0, π/2) and increasing on (π/2, π).
Solution:
f(x) = log cos x
f'(x) = 1/cos x (-sin x) = -tan x
Interval (0, π/2), it is first quadrant, here tan x is positive.
So, f'(x) = -tan x is negative(i.e., tan x < 0)
Hence, f(x) is strictly decreasing in interval (0, π/2)
Interval (π/2, π), it is second quadrant, here tan x is negative.
So, f'(x) = -tan x is positive (i.e., tan x > 0)
Hence, f(x) is strictly increasing in interval (π/2, π)
Question 18. Prove that the function given by f(x) = x3 – 3x2 + 3x – 100 is increasing in R.
Solution:
f(x) = x3 – 3x2 + 3x – 100
f'(x) = 3x2 – 6x + 3
f'(x) = 3(x2 – 2x + 1)
f'(x) = 3(x – 1)2 ≥ 0 ∀ x in R
So f(x) is strictly increasing in R.
Question 19. The interval in which y = x2 e-x is increasing is
(A) (– ∞, ∞) (B) (– 2, 0) (C) (2, ∞) (D) (0, 2)
Solution:
Given, f(x) = x2e-x
f'(x) = x2(-e-x) + e-x.2x
f'(x) = e-x(2x – x2)
f'(x) = e-x.x(2 – x)
For f(x) to be increasing, f'(x) ≥ 0
So, f'(x) ≥ 0
e-x.x.(2 – x) ≥ 0
x.(2 – x) ≥ 0
x(x – 2) ≥ 0
x ∈ [0, 2]
So, the f(x) is strictly increasing in interval (0, 2). Correct option in D.
Share your thoughts in the comments
Please Login to comment...