Class 10 NCERT Solutions – Chapter 10 Circles – Exercise 10.1
Last Updated :
03 May, 2021
Question 1. How many tangents can a circle have?
Solution:
A circle can have an infinite number of tangents because it has a infinite number of points on its circumference and each point can have its individual tangent.
Question 2. Fill in the blanks:
(i) A tangent to a circle intersects it in _______ point (s).
(ii) A line intersecting a circle in two points is called a __________.
(iii) A circle can have __________ parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called ____.
Solution:
(i) one
(ii) secant
(iii) two
(iv) Point of contact
Question 3. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is :
(A) 12 cm (B) 13 cm (C) 8.5 cm (D) √119 cm
Solution:
As we know that the line drawn from the centre of the circle to the tangent is perpendicular to the tangent at the point of the contact.
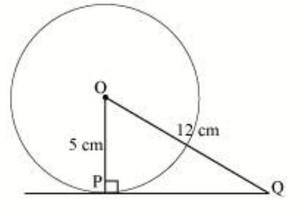
Here OP is perpendicular to PQ.
Hence, the triangle OPQ is a Right angled Triangle, and we can apply Pythagoras Theorem in it.
PQ = √(OQ2−OP2)
PQ = √(122 – 52)cm
PQ = √119 cm
Hence, Option D is the correct answer.
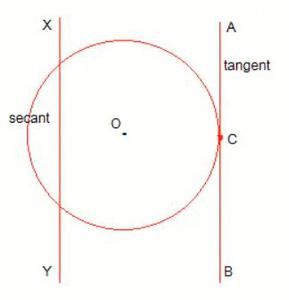
Question 4. Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Solution:
Here AB is the tangent to the circle at point C and XY is the secant to the circle. Also, both lines are parallel.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...