Check whether right angled triangle is valid or not for large sides

Given three integers a, b and c as triplets. Check if it is possible to make right angled triangle or not. Print Yes if possible, else No. 10^-18 <= a, b, c <= 10¹⁸
Examples:

Input: 3 4 5
Output: Yes
Explanation:
Since 3*3 + 4*4 = 5*5
Hence print "Yes"

Input: 8 5 13
Since 8 + 5 < 13 which violates the property of
triangle. Hence print "No"

For a right angled triangle to be valid it must satisfies the following criteria:- 

1. a, b and c should be greater than 0. 
   
2. Sum of any two sides of triangle must be greater than the third side. 
   
3. Pythagorean Theorem i.e., a² + b² = c². 
   

First two conditions can be easily checked but for third condition we have to take care of overflow. Since a, b and c can be large so we can’t compare them directly unless we use python or BigInteger library in Java. For languages like C and C++, we have to reduce the expression in fraction form. 

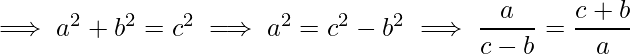
Before comparing the fraction we need convert them in simplified form by dividing the numerator and denominator by gcd of both of them. Now compare both numerator and denominator of both the fractions of LHS and RHS such that if both would become same then it signifies the valid right angled triangle otherwise not.

C++

// C++ program to check validity of triplets
#include <bits/stdc++.h>
using namespace std;

// Function to check pythagorean triplets
bool Triplets(long long a, long long b, long long c)
{
    if (a <= 0 || b <= 0 || c <= 0)
        return false;

    vector<long long> vec{ a, b, c };
    sort(vec.begin(), vec.end());

    // Re-initialize a, b, c in ascending order
    a = vec[0], b = vec[1], c = vec[2];

    // Check validation of sides of triangle
    if (a + b <= c)
        return false;

    long long p1 = a, p2 = c - b;

    // Reduce fraction to simplified form
    long long div = __gcd(p1, p2);
    p1 /= div, p2 /= div;

    long long q1 = c + b, q2 = a;

    // Reduce fraction to simplified form
    div = __gcd(q1, q2);
    q1 /= div, q2 /= div;

    // If fraction are equal return
    // 'true' else 'false'
    return (p1 == q1 && p2 == q2);
}

// Function that will return 'Yes' or 'No'
// according to the correction of triplets
string checkTriplet(long long a, long long b, long long c)
{
    if (Triplets(a, b, c))
        return "Yes";
    else
        return "No";
}

// Driver code
int main()
{
    long long a = 4, b = 3, c = 5;
    cout << checkTriplet(a, b, c) << endl;

    a = 8, b = 13, c = 5;
    cout << checkTriplet(a, b, c) << endl;

    a = 1200000000000, b = 1600000000000,
    c = 2000000000000;
    cout << checkTriplet(a, b, c) << endl;

    return 0;
}

Java

// Java program to check validity of triplets
import java.util.*;

class GFG
{

// Function to check pythagorean triplets
static boolean Triplets(long a,
                        long b, long c)
{
    if (a <= 0 || b <= 0 || c <= 0)
        return false;

    long []vec = { a, b, c };
    Arrays.sort(vec);

    // Re-initialize a, b, c in ascending order
    a = vec[0]; b = vec[1]; c = vec[2];

    // Check validation of sides of triangle
    if (a + b <= c)
        return false;

    long p1 = a, p2 = c - b;

    // Reduce fraction to simplified form
    long div = __gcd(p1, p2);
    p1 /= div; p2 /= div;

    long q1 = c + b, q2 = a;

    // Reduce fraction to simplified form
    div = __gcd(q1, q2);
    q1 /= div; q2 /= div;

    // If fraction are equal return
    // 'true' else 'false'
    return (p1 == q1 && p2 == q2);
}

// Function that will return 'Yes' or 'No'
// according to the correction of triplets
static String checkTriplet(long a,
                           long b, long c)
{
    if (Triplets(a, b, c))
        return "Yes";
    else
        return "No";
}

static long __gcd(long a, long b)
{
    if (b == 0)
        return a;
    return __gcd(b, a % b);

}

// Driver code
public static void main(String[] args)
{
    long a = 4, b = 3, c = 5;
    System.out.println(checkTriplet(a, b, c));

    a = 8; b = 13; c = 5;
    System.out.println(checkTriplet(a, b, c));

    a = 1200000000000L; b = 1600000000000L;
    c = 2000000000000L;
    System.out.println(checkTriplet(a, b, c));
}
}

// This code is contributed
// by Princi Singh

Python3

# Python3 program to check validity of triplets
def Triplets(a, b, c):

    if (a <= 0 or b <= 0 or c <= 0):
        return False

    vec = [ a, b, c ]
    vec.sort()

    # Re - initialize a, b, c in ascending order
    a = vec[0]; b = vec[1]; c = vec[2]

    # Check validation of sides of triangle
    if (a + b <= c):
        return False

    p1 = a; p2 = c - b

    # Reduce fraction to simplified form
    div = __gcd(p1, p2)
    p1 //= div
    p2 //= div

    q1 = c + b
    q2 = a

    # Reduce fraction to simplified form
    div = __gcd(q1, q2)
    q1 //= div
    q2 //= div

    # If fraction are equal return
    # 'true' else 'false'
    return (p1 == q1 and p2 == q2)

# Function that will return 'Yes' or 'No'
# according to the correction of triplets
def checkTriplet(a, b, c):

    if (Triplets(a, b, c)):
        return "Yes"
    else:
        return "No"

def __gcd(a, b):
    if (b == 0):
        return a
    return __gcd(b, a % b)

# Driver code
a = 4
b = 3
c = 5
print(checkTriplet(a, b, c))

a = 8
b = 13
c = 5
print(checkTriplet(a, b, c))

a = 1200000000000
b = 1600000000000
c = 2000000000000
print(checkTriplet(a, b, c))

# This code is contributed by ng24_7

C#

// C# program to check validity of triplets
using System;

class GFG
{

// Function to check pythagorean triplets
static Boolean Triplets(long a,
                        long b, long c)
{
    if (a <= 0 || b <= 0 || c <= 0)
        return false;

    long []vec = { a, b, c };
    Array.Sort(vec);

    // Re-initialize a, b, c in ascending order
    a = vec[0]; b = vec[1]; c = vec[2];

    // Check validation of sides of triangle
    if (a + b <= c)
        return false;

    long p1 = a, p2 = c - b;

    // Reduce fraction to simplified form
    long div = __gcd(p1, p2);
    p1 /= div; p2 /= div;

    long q1 = c + b, q2 = a;

    // Reduce fraction to simplified form
    div = __gcd(q1, q2);
    q1 /= div; q2 /= div;

    // If fraction are equal return
    // 'true' else 'false'
    return (p1 == q1 && p2 == q2);
}

// Function that will return 'Yes' or 'No'
// according to the correction of triplets
static String checkTriplet(long a,
                        long b, long c)
{
    if (Triplets(a, b, c))
        return "Yes";
    else
        return "No";
}

static long __gcd(long a, long b)
{
    if (b == 0)
        return a;
    return __gcd(b, a % b);

}

// Driver code
public static void Main(String[] args)
{
    long a = 4, b = 3, c = 5;
    Console.WriteLine(checkTriplet(a, b, c));

    a = 8; b = 13; c = 5;
    Console.WriteLine(checkTriplet(a, b, c));

    a = 1200000000000L; b = 1600000000000L;
    c = 2000000000000L;
    Console.WriteLine(checkTriplet(a, b, c));
}
}

// This code has been contributed by 29AjayKumar

Javascript

<script>

// Javascript program to check validity of triplets

// Function to check pythagorean triplets
function Triplets(a, b, c)
{
    if (a <= 0 || b <= 0 || c <= 0)
        return false;

    let vec = [ a, b, c ];
    vec.sort();

    // Re-initialize a, b, c in ascending order
    a = vec[0]; b = vec[1]; c = vec[2];

    // Check validation of sides of triangle
    if (a + b <= c)
        return false;

    let p1 = a, p2 = c - b;

    // Reduce fraction to simplified form
    let div = __gcd(p1, p2);
    p1 /= div; p2 /= div;

    let q1 = c + b, q2 = a;

    // Reduce fraction to simplified form
    div = __gcd(q1, q2);
    q1 /= div; q2 /= div;

    // If fraction are equal return
    // 'true' else 'false'
    return (p1 == q1 && p2 == q2);
}

// Function that will return 'Yes' or 'No'
// according to the correction of triplets
function checkTriplet(a, b, c){

    if (Triplets(a, b, c))
        return "Yes";
    else
        return "No";
}

function __gcd(a, b)
{
    if (b == 0)
        return a;
    return __gcd(b, a % b);

}

// driver program
    let a = 4, b = 3, c = 5;
    document.write(checkTriplet(a, b, c) + "<br/>");

    a = 8; b = 13; c = 5;
    document.write(checkTriplet(a, b, c)  + "<br/>");

    a = 1200000000000; b = 1600000000000;
    c = 2000000000000;
    document.write(checkTriplet(a, b, c)  + "<br/>");

// This code is contributed by sanjoy_62.
</script>

Output:

Yes
No
Yes

Time complexity: O(log(M)) where M is the Maximum value among a, b and c. 
Auxiliary space: O(1)
This article is contributed by Shubham Bansal. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.