Given coordinates of three points in a plane P1, P2 and P3, the task is to check if the three points form a triangle or not
Examples:
Input: P1 = (1, 5), P2 = (2, 5), P3 = (4, 6)
Output: Yes
Input: P1 = (1, 1), P2 = (1, 4), P3 = (1, 5)
Output: No
Approach: The key observation in the problem is three points form a triangle only when they don’t lie on the straight line, that is an area formed by the triangle of these three points is not equal to zero.
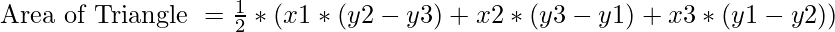
The above formula is derived from shoelace formula.
So we will check if the area formed by the triangle is zero or not.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void checkTriangle(int x1, int y1, int x2,
int y2, int x3, int y3)
{
int a = x1 * (y2 - y3)
+ x2 * (y3 - y1)
+ x3 * (y1 - y2);
if (a == 0)
cout << "No";
else
cout << "Yes";
}
int main()
{
int x1 = 1, x2 = 2, x3 = 3,
y1 = 1, y2 = 2, y3 = 3;
checkTriangle(x1, y1, x2,
y2, x3, y3);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG {
static void checkTriangle(int x1, int y1,
int x2, int y2,
int x3, int y3)
{
int a = x1 * (y2 - y3) +
x2 * (y3 - y1) +
x3 * (y1 - y2);
if (a == 0)
System.out.println("No");
else
System.out.println("Yes");
}
public static void main(String[] args)
{
int x1 = 1, y1 = 1,
x2 = 2, y2 = 2,
x3 = 3, y3 = 3;
checkTriangle(x1, y1, x2, y2, x3, y3);
}
}
|
Python3
def checkTriangle(x1, y1, x2, y2, x3, y3):
a = (x1 * (y2 - y3) +
x2 * (y3 - y1) +
x3 * (y1 - y2))
if a == 0:
print('No')
else:
print('Yes')
if __name__=='__main__':
(x1, x2, x3) = (1, 2, 3)
(y1, y2, y3) = (1, 2, 3)
checkTriangle(x1, y1, x2, y2, x3, y3)
|
C#
using System;
class GFG {
static void checkTriangle(int x1, int y1,
int x2, int y2,
int x3, int y3)
{
int a = x1 * (y2 - y3) +
x2 * (y3 - y1) +
x3 * (y1 - y2);
if (a == 0)
Console.WriteLine("No");
else
Console.WriteLine("Yes");
}
public static void Main()
{
int x1 = 1, y1 = 1,
x2 = 2, y2 = 2,
x3 = 3, y3 = 3;
checkTriangle(x1, y1, x2, y2, x3, y3);
}
}
|
Javascript
<script>
function checkTriangle(x1, y1, x2,
y2, x3, y3)
{
let a = x1 * (y2 - y3)
+ x2 * (y3 - y1)
+ x3 * (y1 - y2);
if (a == 0)
document.write("No");
else
document.write("Yes");
}
let x1 = 1, x2 = 2, x3 = 3,
y1 = 1, y2 = 2, y3 = 3;
checkTriangle(x1, y1, x2,
y2, x3, y3);
</script>
|
Time Complexity: O(1)
Auxiliary Space : O(1)
Approach#2: Using the Triangle Inequality Theorem
One way to check if a triangle is valid is to use the triangle inequality theorem. According to this theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. Therefore, if we calculate the lengths of all three sides of the triangle and check if this condition is satisfied, we can determine if the triangle is valid or not.
Algorithm
1. Define a function valid_triangle(p1, p2, p3) that takes the three points as input.
2. Calculate the lengths of all three sides of the triangle using the distance formula.
3. Check if the sum of the lengths of any two sides is greater than the length of the third side.
4. If this condition is satisfied for all three combinations of sides, the triangle is valid; otherwise, it is invalid.
Java
import java.io.*;
public class Main {
public static double distance(double[] p1, double[] p2) {
return Math.sqrt(Math.pow(p2[0] - p1[0], 2) + Math.pow(p2[1] - p1[1], 2));
}
public static boolean validTriangle(double[] p1, double[] p2, double[] p3) {
double d1 = distance(p1, p2);
double d2 = distance(p2, p3);
double d3 = distance(p3, p1);
return d1 + d2 > d3 && d2 + d3 > d1 && d3 + d1 > d2;
}
public static void main(String[] args) {
double[] P1 = {1, 5};
double[] P2 = {2, 5};
double[] P3 = {4, 6};
System.out.println(validTriangle(P1, P2, P3));
double[] P4 = {1, 1};
double[] P5 = {1, 4};
double[] P6 = {1, 5};
System.out.println(validTriangle(P4, P5, P6));
}
}
|
Python3
from math import sqrt
def distance(p1, p2):
return sqrt((p2[0] - p1[0])**2 + (p2[1] - p1[1])**2)
def valid_triangle(p1, p2, p3):
d1 = distance(p1, p2)
d2 = distance(p2, p3)
d3 = distance(p3, p1)
return d1 + d2 > d3 and d2 + d3 > d1 and d3 + d1 > d2
P1 = (1, 5)
P2 = (2, 5)
P3 = (4, 6)
print(valid_triangle(P1, P2, P3))
P1 = (1, 1)
P2 = (1, 4)
P3 = (1, 5)
print(valid_triangle(P1, P2, P3))
|
Javascript
function distance(p1, p2) {
return Math.sqrt((p2[0] - p1[0]) ** 2 + (p2[1] - p1[1]) ** 2);
}
function validTriangle(p1, p2, p3) {
const d1 = distance(p1, p2);
const d2 = distance(p2, p3);
const d3 = distance(p3, p1);
return d1 + d2 > d3 && d2 + d3 > d1 && d3 + d1 > d2;
}
const P1 = [1, 5];
const P2 = [2, 5];
const P3 = [4, 6];
console.log(validTriangle(P1, P2, P3));
const P4 = [1, 1];
const P5 = [1, 4];
const P6 = [1, 5];
console.log(validTriangle(P4, P5, P6));
|
Time Complexity: O(1)
Space Complexity: O(1)