Check if it is possible to create a polygon with a given angle
Last Updated :
31 Aug, 2022
Given an angle 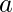 where,
where, 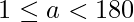 . The task is to check whether it is possible to make a regular polygon with all of its interior angle equal to
. The task is to check whether it is possible to make a regular polygon with all of its interior angle equal to 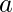 . If possible then print “YES”, otherwise print “NO” (without quotes).
. If possible then print “YES”, otherwise print “NO” (without quotes).
Examples:
Input: angle = 90
Output: YES
Polygons with sides 4 is
possible with angle 90 degrees.
Input: angle = 30
Output: NO
Approach: The Interior angle is defined as the angle between any two adjacent sides of a regular polygon.
It is given by 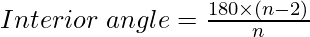 where, n is the number of sides in the polygon.
where, n is the number of sides in the polygon.
This can be written as 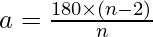 .
.
On rearranging terms we get, 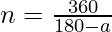 .
.
Thus, if n is an Integer the answer is “YES” otherwise, answer is “NO”.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void makePolygon(float a)
{
float n = 360 / (180 - a);
if (n == (int)n)
cout << "YES";
else
cout << "NO";
}
int main()
{
float a = 90;
makePolygon(a);
return 0;
}
|
Java
class GFG
{
static void makePolygon(double a)
{
double n = 360 / (180 - a);
if (n == (int)n)
System.out.println("YES");
else
System.out.println("NO");
}
public static void main (String[] args)
{
double a = 90;
makePolygon(a);
}
}
|
Python3
def makePolygon(a) :
n = 360 / (180 - a)
if n == int(n) :
print("YES")
else :
print("NO")
if __name__ == "__main__" :
a = 90
makePolygon(a)
|
C#
using System;
class GFG
{
static void makePolygon(double a)
{
double n = 360 / (180 - a);
if (n == (int)n)
Console.WriteLine("YES");
else
Console.WriteLine("NO");
}
static void Main()
{
double a = 90;
makePolygon(a);
}
}
|
PHP
<?php
function makePolygon($a)
{
$n = 360 / (180 - $a);
if ($n == (int)$n)
echo "YES";
else
echo "NO";
}
$a = 90;
makePolygon($a);
?>
|
Javascript
<script>
function makePolygon(a)
{
var n = parseFloat(360 / (180 - a));
if (n === parseInt(n))
document.write("YES");
else
document.write("NO");
}
var a = 90;
makePolygon(a);
</script>
|
Time Complexity: O(1), since there is no loop or recursion.
Auxiliary Space: O(1), since no extra space has been taken.
Share your thoughts in the comments
Please Login to comment...