Centroid Decomposition of Tree
Last Updated :
26 Oct, 2023
Background : What is centroid of Tree?
Centroid of a Tree is a node which if removed from the tree would split it into a ‘forest’, such that any tree in the forest would have at most half the number of vertices in the original tree.
Suppose there are n nodes in the tree. ‘Subtree size’ for a node is the size of the tree rooted at the node.
Let S(v) be size of subtree rooted at node v
S(v) = 1 + ? S(u)
Here u is a child to v (adjacent and at a depth one
greater than the depth of v).
Centroid is a node v such that,
maximum(n - S(v), S(u1), S(u2), .. S(um)) <= n/2
where ui is i'th child to v.
Finding the centroid
Let T be an undirected tree with n nodes. Choose any arbitrary node v in the tree. If v satisfies the mathematical definition for the centroid, we have our centroid. Else, we know that our mathematical inequality did not hold, and from this, we conclude that there exists some u adjacent to v such that S(u) > n/2. We make that u our new v and recurse.

We never revisit a node because when we decided to move away from it to a node with subtree size greater than n/2, we sort of declared that it now belongs to the component with nodes less than n/2, and we shall never find our centroid there.
In any case we are moving towards the centroid. Also, there are finitely many vertices in the tree. The process must stop, and it will, at the desired vertex.
Algorithm :
- Select arbitrary node v
- Start a DFS from v, and setup subtree sizes
- Re-position to node v (or start at any arbitrary v that belongs to the tree)
- Check mathematical condition of centroid for v
- If condition passed, return current node as centroid
- Else move to adjacent node with ‘greatest’ subtree size, and back to step 4
Theorem: Given a tree with n nodes, the centroid always exists.
Proof: Clear from our approach to the problem that we can always find a centroid using above steps.
Time Complexity
- Select arbitrary node v: O(1)
- DFS: O(n)
- Reposition to v: O(1)
- Find centroid: O(n)
Centroid Decomposition :
Finding the centroid for a tree is a part of what we are trying to achieve here. We need to think how can we organize the tree into a structure that decreases the complexity for answering certain ‘type’ of queries.
Algorithm
- Make the centroid as the root of a new tree (which we will call as the ‘centroid tree’)
- Recursively decompose the trees in the resulting forest
- Make the centroids of these trees as children of the centroid which last split them.
The centroid tree has depth O(log n), and can be constructed in O(n lg n), as we can find the centroid in O(n).
Illustrative Example
Let us consider a tree with 16 nodes. The figure has subtree sizes already set up using a DFS from node 1.

We start at node 1 and see if condition for centroid holds. Remember S(v) is subtree size for v.
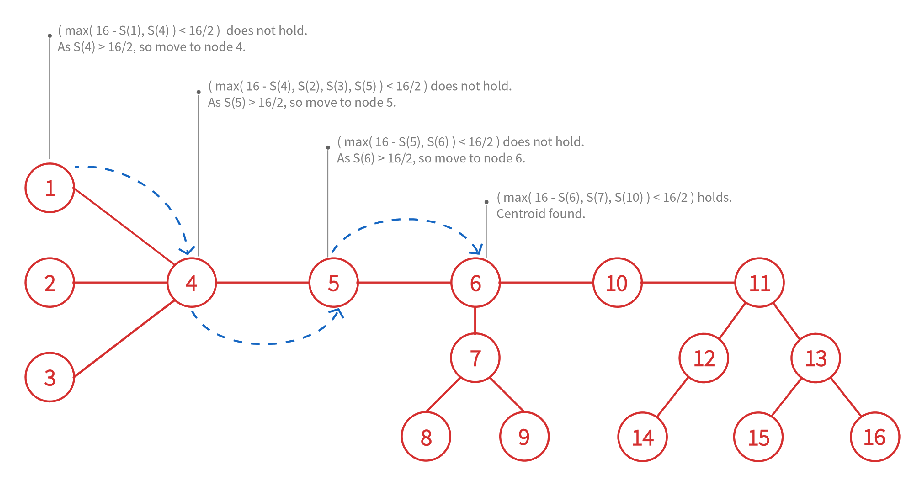
We make node 6 as the root of our centroid, and recurse on the 3 trees of the forest centroid split the original tree into.
NOTE: In the figure, subtrees generated by a centroid have been surrounded by a dotted line of the same color as the color of centroid.

We make the subsequently found centroids as the children to centroid that split them last, and obtain our centroid tree.

NOTE: The trees containing only a single element have the same element as their centroid. We haven’t used color differentiation for such trees, and the leaf nodes represent them.
C++
#include <bits/stdc++.h>
using namespace std;
#define MAXN 1025
vector<int> tree[MAXN];
vector<int> centroidTree[MAXN];
bool centroidMarked[MAXN];
void addEdge(int u, int v)
{
tree[u].push_back(v);
tree[v].push_back(u);
}
void DFS(int src, bool visited[], int subtree_size[], int* n)
{
visited[src] = true;
*n += 1;
subtree_size[src] = 1;
vector<int>::iterator it;
for (it = tree[src].begin(); it!=tree[src].end(); it++)
if (!visited[*it] && !centroidMarked[*it])
{
DFS(*it, visited, subtree_size, n);
subtree_size[src]+=subtree_size[*it];
}
}
int getCentroid(int src, bool visited[], int subtree_size[], int n)
{
bool is_centroid = true;
visited[src] = true;
int heaviest_child = 0;
vector<int>::iterator it;
for (it = tree[src].begin(); it!=tree[src].end(); it++)
if (!visited[*it] && !centroidMarked[*it])
{
if (subtree_size[*it]>n/2)
is_centroid=false;
if (heaviest_child==0 ||
subtree_size[*it]>subtree_size[heaviest_child])
heaviest_child = *it;
}
if (is_centroid && n-subtree_size[src]<=n/2)
return src;
return getCentroid(heaviest_child, visited, subtree_size, n);
}
int getCentroid(int src)
{
bool visited[MAXN];
int subtree_size[MAXN];
memset(visited, false, sizeof visited);
memset(subtree_size, 0, sizeof subtree_size);
int n = 0;
DFS(src, visited, subtree_size, &n);
for (int i=1; i<MAXN; i++)
visited[i] = false;
int centroid = getCentroid(src, visited, subtree_size, n);
centroidMarked[centroid]=true;
return centroid;
}
int decomposeTree(int root)
{
int cend_tree = getCentroid(root);
printf("%d ", cend_tree);
vector<int>::iterator it;
for (it=tree[cend_tree].begin(); it!=tree[cend_tree].end(); it++)
{
if (!centroidMarked[*it])
{
int cend_subtree = decomposeTree(*it);
centroidTree[cend_tree].push_back(cend_subtree);
centroidTree[cend_subtree].push_back(cend_tree);
}
}
return cend_tree;
}
int main()
{
int n = 16;
addEdge(1, 4);
addEdge(2, 4);
addEdge(3, 4);
addEdge(4, 5);
addEdge(5, 6);
addEdge(6, 7);
addEdge(7, 8);
addEdge(7, 9);
addEdge(6, 10);
addEdge(10, 11);
addEdge(11, 12);
addEdge(11, 13);
addEdge(12, 14);
addEdge(13, 15);
addEdge(13, 16);
decomposeTree(1);
return 0;
}
|
Java
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class CentroidDecomposition {
static final int MAXN = 1025;
static List<Integer>[] tree = new ArrayList[MAXN];
static List<Integer>[] centroidTree = new ArrayList[MAXN];
static boolean[] centroidMarked = new boolean[MAXN];
static void addEdge(int u, int v) {
tree[u].add(v);
tree[v].add(u);
}
static void DFS(int src, boolean[] visited, int[] subtreeSize, int[] n) {
visited[src] = true;
n[0]++;
subtreeSize[src] = 1;
for (int neighbor : tree[src]) {
if (!visited[neighbor] && !centroidMarked[neighbor]) {
DFS(neighbor, visited, subtreeSize, n);
subtreeSize[src] += subtreeSize[neighbor];
}
}
}
static int getCentroid(int src) {
boolean[] visited = new boolean[MAXN];
int[] subtreeSize = new int[MAXN];
Arrays.fill(visited, false);
Arrays.fill(subtreeSize, 0);
int[] n = {0};
DFS(src, visited, subtreeSize, n);
Arrays.fill(visited, false);
int centroid = getCentroid(src, visited, subtreeSize, n[0]);
centroidMarked[centroid] = true;
return centroid;
}
static int getCentroid(int src, boolean[] visited, int[] subtreeSize, int n) {
boolean isCentroid = true;
visited[src] = true;
int heaviestChild = 0;
for (int neighbor : tree[src]) {
if (!visited[neighbor] && !centroidMarked[neighbor]) {
if (subtreeSize[neighbor] > n / 2)
isCentroid = false;
if (heaviestChild == 0 || subtreeSize[neighbor] > subtreeSize[heaviestChild])
heaviestChild = neighbor;
}
}
if (isCentroid && n - subtreeSize[src] <= n / 2)
return src;
return getCentroid(heaviestChild, visited, subtreeSize, n);
}
static int decomposeTree(int root) {
int cendTree = getCentroid(root);
System.out.print(cendTree + " ");
for (int neighbor : tree[cendTree]) {
if (!centroidMarked[neighbor]) {
int cendSubtree = decomposeTree(neighbor);
centroidTree[cendTree].add(cendSubtree);
centroidTree[cendSubtree].add(cendTree);
}
}
return cendTree;
}
public static void main(String[] args) {
int n = 16;
for (int i = 0; i < MAXN; i++) {
tree[i] = new ArrayList<>();
centroidTree[i] = new ArrayList<>();
}
addEdge(1, 4);
addEdge(2, 4);
addEdge(3, 4);
addEdge(4, 5);
addEdge(5, 6);
addEdge(6, 7);
addEdge(7, 8);
addEdge(7, 9);
addEdge(6, 10);
addEdge(10, 11);
addEdge(11, 12);
addEdge(11, 13);
addEdge(12, 14);
addEdge(13, 15);
addEdge(13, 16);
decomposeTree(1);
}
}
|
Python3
import collections
MAXN = 1025
tree = collections.defaultdict(list)
centroidTree = collections.defaultdict(list)
centroidMarked = [False]*MAXN
def addEdge(u, v):
tree[u].append(v)
tree[v].append(u)
def DFS(src, visited, subtree_size, n):
visited[src] = True
n[0] += 1
subtree_size[src] = 1
for it in tree[src]:
if not visited[it] and not centroidMarked[it]:
DFS(it, visited, subtree_size, n)
subtree_size[src] += subtree_size[it]
def getCentroid(src, visited, subtree_size, n):
is_centroid = True
visited[src] = True
heaviest_child = 0
for it in tree[src]:
if not visited[it] and not centroidMarked[it]:
if subtree_size[it] > n/2:
is_centroid = False
if heaviest_child == 0 or subtree_size[it] > subtree_size[heaviest_child]:
heaviest_child = it
if is_centroid and n - subtree_size[src] <= n/2:
return src
return getCentroid(heaviest_child, visited, subtree_size, n)
def getCentroidTree(src):
visited = [False]*MAXN
subtree_size = [0]*MAXN
n = [0]
DFS(src, visited, subtree_size, n)
visited = [False]*MAXN
centroid = getCentroid(src, visited, subtree_size, n[0])
centroidMarked[centroid] = True
return centroid
def decomposeTree(root):
cend_tree = getCentroidTree(root)
print(cend_tree, end=" ")
for it in tree[cend_tree]:
if not centroidMarked[it]:
decomposeTree(it)
if __name__ == "__main__":
n = 16
addEdge(1, 4)
addEdge(2, 4)
addEdge(3, 4)
addEdge(4, 5)
addEdge(5, 6)
addEdge(6, 7)
addEdge(7, 8)
addEdge(7, 9)
addEdge(6, 10)
addEdge(10, 11)
addEdge(11, 12)
addEdge(11, 13)
addEdge(12, 14)
addEdge(13, 15)
addEdge(13, 16)
decomposeTree(1)
|
C#
using System;
using System.Collections.Generic;
namespace CentroidDecomposition {
class Program {
static List<int>[] tree = new List<int>[ 1025 ];
static List<int>[] centroidTree = new List<int>[ 1025 ];
static bool[] centroidMarked = new bool[1025];
static void AddEdge(int u, int v)
{
tree[u].Add(v);
tree[v].Add(u);
}
static void DFS(int src, bool[] visited,
int[] subtree_size, ref int n)
{
visited[src] = true;
n++;
subtree_size[src] = 1;
foreach(int neighbour in tree[src])
{
if (!visited[neighbour]
&& !centroidMarked[neighbour]) {
DFS(neighbour, visited, subtree_size,
ref n);
subtree_size[src]
+= subtree_size[neighbour];
}
}
}
static int GetCentroid(int src, bool[] visited,
int[] subtree_size, int n)
{
bool is_centroid = true;
visited[src] = true;
int heaviest_child = 0;
foreach(int neighbour in tree[src])
{
if (!visited[neighbour]
&& !centroidMarked[neighbour]) {
if (subtree_size[neighbour] > n / 2) {
is_centroid = false;
}
if (heaviest_child == 0
|| subtree_size[neighbour]
> subtree_size[heaviest_child]) {
heaviest_child = neighbour;
}
}
}
if (is_centroid && n - subtree_size[src] <= n / 2) {
return src;
}
return GetCentroid(heaviest_child, visited,
subtree_size, n);
}
static int GetCentroid(int src)
{
bool[] visited = new bool[1025];
int[] subtree_size = new int[1025];
Array.Fill(visited, false);
Array.Fill(subtree_size, 0);
int n = 0;
DFS(src, visited, subtree_size, ref n);
Array.Fill(visited, false);
int centroid
= GetCentroid(src, visited, subtree_size, n);
centroidMarked[centroid] = true;
return centroid;
}
static int DecomposeTree(int root)
{
int cend_tree = GetCentroid(root);
Console.Write(cend_tree + " ");
foreach(int adjNode in tree[cend_tree])
{
if (!centroidMarked[adjNode]) {
int cend_subtree = DecomposeTree(adjNode);
centroidTree[cend_tree].Add(cend_subtree);
centroidTree[cend_subtree].Add(cend_tree);
}
}
return cend_tree;
}
public static void Main(string[] args)
{
int n = 16;
for (int i = 0; i < 1025; i++) {
tree[i] = new List<int>();
centroidTree[i] = new List<int>();
}
AddEdge(1, 4);
AddEdge(2, 4);
AddEdge(3, 4);
AddEdge(4, 5);
AddEdge(5, 6);
AddEdge(6, 7);
AddEdge(7, 8);
AddEdge(7, 9);
AddEdge(6, 10);
AddEdge(10, 11);
AddEdge(11, 12);
AddEdge(11, 13);
AddEdge(12, 14);
AddEdge(13, 15);
AddEdge(13, 16);
DecomposeTree(1);
}
}
}
|
Javascript
const MAXN = 1025;
const tree = {};
const centroidTree = {};
const centroidMarked = new Array(MAXN).fill(false);
function addEdge(u, v) {
if (!tree[u]) tree[u] = [];
if (!tree[v]) tree[v] = [];
tree[u].push(v);
tree[v].push(u);
}
function DFS(src, visited, subtree_size, n) {
visited[src] = true;
n[0] += 1;
subtree_size[src] = 1;
for (let i = 0; i < tree[src].length; i++) {
const it = tree[src][i];
if (!visited[it] && !centroidMarked[it]) {
DFS(it, visited, subtree_size, n);
subtree_size[src] += subtree_size[it];
}
}
}
function getCentroid(src, visited, subtree_size, n) {
let is_centroid = true;
visited[src] = true;
let heaviest_child = 0;
for (let i = 0; i < tree[src].length; i++) {
const it = tree[src][i];
if (!visited[it] && !centroidMarked[it]) {
if (subtree_size[it] > n / 2) {
is_centroid = false;
}
if (heaviest_child == 0 || subtree_size[it] > subtree_size[heaviest_child]) {
heaviest_child = it;
}
}
}
if (is_centroid && n - subtree_size[src] <= n / 2) {
return src;
}
return getCentroid(heaviest_child, visited, subtree_size, n);
}
function getCentroidTree(src) {
const visited = new Array(MAXN).fill(false);
const subtree_size = new Array(MAXN).fill(0);
const n = [0];
DFS(src, visited, subtree_size, n);
visited.fill(false);
const centroid = getCentroid(src, visited, subtree_size, n[0]);
centroidMarked[centroid] = true;
return centroid;
}
function decomposeTree(root) {
const cend_tree = getCentroidTree(root);
process.stdout.write(cend_tree + " ");
centroidMarked[cend_tree] = true;
for (let i = 0; i < tree[cend_tree].length; i++) {
const it = tree[cend_tree][i];
if (!centroidMarked[it]) {
decomposeTree(it);
}
}
}
const n = 16;
addEdge(1, 4);
addEdge(2, 4);
addEdge(3, 4);
addEdge(4, 5);
addEdge(5, 6);
addEdge(6, 7);
addEdge(7, 8);
addEdge(7, 9);
addEdge(6, 10);
addEdge(10, 11);
addEdge(11, 12);
addEdge(11, 13);
addEdge(12, 14);
addEdge(13, 15);
addEdge(13, 16);
decomposeTree(1);
|
Output :
6 4 1 2 3 5 7 8 9 11 10 12 14 13 15 16
Application:
Consider below example problem
Given a weighted tree with N nodes, find the minimum number
of edges in a path of length K, or return -1 if such a path
does not exist.
1 <= N <= 200000
1 <= length(i;j) <= 1000000 (integer weights)
1 <= K <= 1000000
Brute force solution: For every node, perform DFS to find distance and number of edges to every other node
Time complexity: O(N2) Obviously inefficient because N = 200000
We can solve above problem in O(N Log N) time using Centroid Decomposition.
- Perform centroid decomposition to get a “tree of subtrees”
- Start at the root of the decomposition, solve the problem for each subtree as follows
- Solve the problem for each “child tree” of the current subtree.
- Perform DFS from the centroid on the current subtree to compute the minimum edge count for paths that include the centroid
- Two cases: centroid at the end or in the middle of the path
Time complexity of centroid decomposition based solution is O(n log n)
Reference :
http://www.ugrad.cs.ubc.ca/~cs490/2014W2/pdf/jason.pdf
This article is contributed by Yash Varyani.
Share your thoughts in the comments
Please Login to comment...