Sum of decomposition values of all suffixes of an Array

Given an array arr[], the task is to find the sum of the decomposition value of the suffixes subarray.
Decomposition Value: The decomposition value of a subarray is the count of the partition in the subarray possible. The partition in the array at index 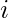can be done only if the elements of the array before if it less than the current index. That is A[k] < A[i], where k ? i.
Examples:

Input: arr[] = {2, 8, 4} 
Output: 4 
Explanation:
All suffixes subarray of arr[] are [2, 8, 4], [8, 4], [4] 
Suffix [4] => only 1 decomposition {4}
Suffix [8, 4] => only 1 decomposition {8, 4}
Suffix [2, 8, 4] => 2 decompositions {2, 8, 4}, {2} {8, 4}
Hence, Sum of Decomposition values = 1 + 1 + 2 = 4
Input: arr[] = {9, 6, 9, 35} 
Output: 8 
Explanation:
All suffixes of arr are [9, 6, 9, 35], [6, 9, 35], [9, 35], [35] 
Suffix [35] => only 1 decomposition {35}
Suffix [9, 35] => 2 decompositions {9} {35}
Suffix [6, 9, 35] => 3 decompositions {6} {9, 35} 
Suffix [9, 6, 9, 35] => 2 decompositions {9, 6, 9} {35} 
Hence, Sum of Decomposition values = 1 + 2 + 3 + 2 = 8 

Approach: The idea is to use Stack to solve this problem. Below is the illustration of the approach

• Traverse array from the end to the start.
• Maintain a minimum variable and answer variable.
• If the stack is empty or the current element is less than the top of stack – 
  
  • Push S[i] onto the stack.
  • Increment the answer by the size of the stack.
  • Also, maintain the minimum value till now.
• Otherwise, 
  
  • Keep on popping the blocks as long as top of the stack is less than the current element.
  • Update the minimum value till now with the current element.
  • Push minimum value onto the stack. Because, we want the minimum value of the subarray to represent that subarray
  • Increment the answer by the size of the stack.

Below is the implementation of the above approach:

C++

// C++ implementation to find the
// sum of Decomposition values of
// all suffixes of an array

#include <bits/stdc++.h>
using namespace std;
#define int long long int

// Function to find the decomposition
// values of the array
int decompose(vector<int> S)
{
    // Stack
    stack<int> s;
    int N = S.size();
    int ans = 0;

    // Variable to maintain
    // min value in stack
    int nix = INT_MAX;

    // Loop to iterate over the array
    for (int i = N - 1; i >= 0; i--) {

        // Condition to check if the
        // stack is empty
        if (s.empty()) {
            s.push(S[i]);
            nix = S[i];
        }
        else {

            // Condition to check if the
            // top of the stack is greater
            // than the current element
            if (S[i] < s.top()) {
                s.push(S[i]);
                nix = min(nix, S[i]);
            }
            else {
                int val = S[i];

                // Loop to pop the element out
                while (!s.empty() &&
                       val >= s.top()) {
                    s.pop();
                }
                nix = min(nix, S[i]);
                s.push(nix);
            }
        }

        // the size of the stack is the
        // max no of subarrays for
        // suffix till index i
        // from the right
        ans += s.size();
    }

    return ans;
}

// Driver Code
signed main()
{
    vector<int> S = { 9, 6, 9, 35 };
    cout << decompose(S) << endl;
    return 0;
}

Java

// Java implementation to find the
// sum of Decomposition values of
// all suffixes of an array
import java.util.*;

class GFG{

// Function to find the decomposition
// values of the array
static int decompose(Vector<Integer> S)
{

    // Stack
    Stack<Integer> s = new Stack<Integer>();
    int N = S.size();
    int ans = 0;

    // Variable to maintain
    // min value in stack
    int nix = Integer.MAX_VALUE;

    // Loop to iterate over the array
    for(int i = N - 1; i >= 0; i--)
    {

       // Condition to check if the
       // stack is empty
       if (s.isEmpty())
       {
           s.add(S.get(i));
           nix = S.get(i);
       }
       else
       {

           // Condition to check if the
           // top of the stack is greater
           // than the current element
           if (S.get(i) < s.peek())
           {
               s.add(S.get(i));
               nix = Math.min(nix, S.get(i));
           }
           else
           {
               int val = S.get(i);

               // Loop to pop the element out
               while (!s.isEmpty() && val >= s.peek())
               {
                   s.pop();
               }
               nix = Math.min(nix, S.get(i));
               s.add(nix);
           }
       }

       // The size of the stack is the
       // max no of subarrays for
       // suffix till index i
       // from the right
       ans += s.size();
    }
    return ans;
}

// Driver Code
public static void main(String args[])
{
    Vector<Integer> S = new Vector<Integer>();
    S.add(9);
    S.add(6);
    S.add(9);
    S.add(35);

    System.out.println(decompose(S));
}
}

// This code is contributed by 29AjayKumar

Python3

# Python3 implementation to find the
# sum of Decomposition values of
# all suffixes of an array
import sys

# Function to find the decomposition
# values of the array
def decompose(S):

    # Stack
    s = []
    N = len(S)
    ans = 0

    # Variable to maintain
    # min value in stack
    nix = sys.maxsize

    # Loop to iterate over the array
    for i in range(N - 1, -1, -1):

        # Condition to check if the
        # stack is empty
        if (len(s) == 0):
            s.append(S[i])
            nix = S[i]

        else:

            # Condition to check if the
            # top of the stack is greater
            # than the current element
            if (S[i] < s[-1]):
                s.append(S[i])
                nix = min(nix, S[i])

            else:
                val = S[i]

                # Loop to pop the element out
                while (len(s) != 0 and
                          val >= s[-1]):
                    s.pop()

                nix = min(nix, S[i]);
                s.append(nix)

        # The size of the stack is the
        # max no of subarrays for
        # suffix till index i
        # from the right
        ans += len(s)

    return ans

# Driver Code
if __name__ =="__main__":

    S = [ 9, 6, 9, 35 ]

    print(decompose(S))

# This code is contributed by chitranayal

C#

// C# implementation to find the
// sum of Decomposition values of
// all suffixes of an array
using System;
using System.Collections.Generic;

class GFG{

// Function to find the decomposition
// values of the array
static int decompose(List<int> S)
{

    // Stack
    Stack<int> s = new Stack<int>();

    int N = S.Count;
    int ans = 0;

    // Variable to maintain
    // min value in stack
    int nix = Int32.MaxValue;

    // Loop to iterate over the array
    for(int i = N - 1; i >= 0; i--)
    {

        // Condition to check if the
        // stack is empty
        if (s.Count == 0)
        {
            s.Push(S[i]);
            nix = S[i];
        }
        else
        {

            // Condition to check if the
            // top of the stack is greater
            // than the current element
            if (S[i] < s.Peek())
            {
                s.Push(S[i]);
                nix = Math.Min(nix, S[i]);
            }
            else
            {
                int val = S[i];

                // Loop to pop the element out
                while (s.Count != 0 && val >= s.Peek())
                {
                    s.Pop();
                }
                nix = Math.Min(nix, S[i]);
                s.Push(nix);
            }
        }

        // The size of the stack is the
        // max no of subarrays for
        // suffix till index i
        // from the right
        ans += s.Count;
    }
    return ans;
}

// Driver code
static void Main()
{
    List<int> S = new List<int>();
    S.Add(9);
    S.Add(6);
    S.Add(9);
    S.Add(35);

    Console.WriteLine(decompose(S));
}
}

// This code is contributed by divyeshrabadiya07

Javascript

<script>
// Javascript implementation to find the
// sum of Decomposition values of
// all suffixes of an array

// Function to find the decomposition
// values of the array
function decompose(S)
{

    // Stack
    let s = [];
    let N = S.length;
    let ans = 0;

    // Variable to maintain
    // min value in stack
    let nix = Number.MAX_VALUE;

    // Loop to iterate over the array
    for(let i = N - 1; i >= 0; i--)
    {

       // Condition to check if the
       // stack is empty
       if (s.length==0)
       {
           s.push(S[i]);
           nix = S[i];
       }
       else
       {

           // Condition to check if the
           // top of the stack is greater
           // than the current element
           if (S[i] < s[s.length-1])
           {
               s.push(S[i]);
               nix = Math.min(nix, S[i]);
           }
           else
           {
               let val = S[i];

               // Loop to pop the element out
               while (s.length!=0 && val >= s[s.length-1])
               {
                   s.pop();
               }
               nix = Math.min(nix, S[i]);
               s.push(nix);
           }
       }

       // The size of the stack is the
       // max no of subarrays for
       // suffix till index i
       // from the right
       ans += s.length;
    }
    return ans;
}

// Driver Code
let S = [];
S.push(9);
S.push(6);
S.push(9);
S.push(35);

document.write(decompose(S));

// This code is contributed by avanitrachhadiya2155
</script>

Output:

8

Time Complexity: O(n)
Auxiliary Space: O(n), where n is the size of the given array.