In R, there are several packages available that provide functions and tools to perform various tasks related to data analysis and visualization. The “car” package is one of the packages that provide functions and tools for regression analysis. In this article, we will provide a comprehensive and in-depth guide to the “car” package in R, including how to install and load the package, how to use the functions it provides, and how to visualize the results.
Installing the “car” Package
Before we can start using the functions provided by the “car” package, we need to install it. Installing the “car” package can be done using the following code:
install.packages("car")
Loading the “car” Package
Once the “car” package is installed, we need to load it into the R environment. Loading the “car” package can be done using the following code:
library(car)
Example 1: Simple Linear Regression
Step 1: Data Preparation
For just demonstration purposes, we will use the “mtcars” dataset that is available in the R environment. The “mtcars” contains data on 32 different models of cars and includes information like miles per gallon (mpg), number of cylinders (cyl), horsepower (hp), weight (wt), and acceleration (qsec).
Output:
mpg cyl disp hp
Min. :10.40 Min. :4.000 Min. : 71.1 Min. : 52.0
1st Qu.:15.43 1st Qu.:4.000 1st Qu.:120.8 1st Qu.: 96.5
Median :19.20 Median :6.000 Median :196.3 Median :123.0
Mean :20.09 Mean :6.188 Mean :230.7 Mean :146.7
3rd Qu.:22.80 3rd Qu.:8.000 3rd Qu.:326.0 3rd Qu.:180.0
Max. :33.90 Max. :8.000 Max. :472.0 Max. :335.0
drat wt qsec vs
Min. :2.760 Min. :1.513 Min. :14.50 Min. :0.0000
1st Qu.:3.080 1st Qu.:2.581 1st Qu.:16.89 1st Qu.:0.0000
Median :3.695 Median :3.325 Median :17.71 Median :0.0000
Mean :3.597 Mean :3.217 Mean :17.85 Mean :0.4375
3rd Qu.:3.920 3rd Qu.:3.610 3rd Qu.:18.90 3rd Qu.:1.0000
Max. :4.930 Max. :5.424 Max. :22.90 Max. :1.0000
am gear carb
Min. :0.0000 Min. :3.000 Min. :1.000
1st Qu.:0.0000 1st Qu.:3.000 1st Qu.:2.000
Median :0.0000 Median :4.000 Median :2.000
Mean :0.4062 Mean :3.688 Mean :2.812
3rd Qu.:1.0000 3rd Qu.:4.000 3rd Qu.:4.000
Max. :1.0000 Max. :5.000 Max. :8.000
Step 2: Simple Linear Regression
The “car” package provides functions for performing linear regression analysis. To perform simple linear regression analysis, we can use the lm() function. For example, if we want to perform a simple linear regression analysis to predict the miles per gallon (mpg) of a car based on its weight (wt), we can use the following code:
R
model <- lm(mpg ~ wt, data = mtcars)
|
Step 3: Model Summary
Once we have fit a linear regression model, we can get a summary of the model using the summary() function. The summary of the model provides information such as the coefficients of the regression equation, the R-squared value, and the p-value of the regression coefficients. To get the summary of the model, we can use the following code:
Output:
Call:
lm(formula = mpg ~ wt, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-4.5432 -2.3647 -0.1252 1.4096 6.8727
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 37.2851 1.8776 19.858 < 2e-16 ***
wt -5.3445 0.5591 -9.559 1.29e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.046 on 30 degrees of freedom
Multiple R-squared: 0.7528, Adjusted R-squared: 0.7446
F-statistic: 91.38 on 1 and 30 DF, p-value: 1.294e-10
Step 4: Plotting the Regression Line
The “car” package also provides functions for visualizing the results of the regression analysis. To plot the regression line, we can use the abline() function. The abline() function takes the parameters of the regression equation as inputs and plots the regression line on a scatter plot of the data. To plot the regression line, we can use the following code:
R
plot(mtcars$wt, mtcars$mpg)
abline(model)
|
Output:
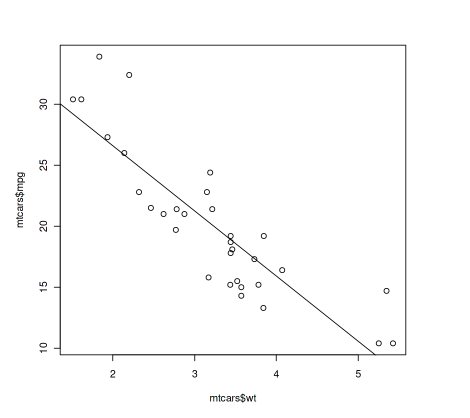
Regression line with scatter plot
Step 5: Residual Plot
The residual plot is a plot of the residuals (the differences between the observed values and the predicted values) against the fitted values. The residual plot can be used to assess the assumptions of the linear regression model, such as the assumption of homoscedasticity (constant variance of the residuals). To plot the residual plot, we can use the residplot() function provided by the “car” package. The residplot() function takes the linear regression model as an input and plots the residual
Output:
Test stat Pr(>|Test stat|)
wt 3.258 0.002860 **
Tukey test 3.258 0.001122 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Pearson Residual for wt, and Fitted values
Example 2: Multiple Linear Regression
Step 1: Fit a multiple linear regression model to predict mpg based on wt and hp
R
library(car)
model <- lm(mpg ~ wt + hp, data = mtcars)
summary(model)
|
Output:
Call:
lm(formula = mpg ~ wt + hp, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-3.941 -1.600 -0.182 1.050 5.854
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 37.22727 1.59879 23.285 < 2e-16 ***
wt -3.87783 0.63273 -6.129 1.12e-06 ***
hp -0.03177 0.00903 -3.519 0.00145 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.593 on 29 degrees of freedom
Multiple R-squared: 0.8268, Adjusted R-squared: 0.8148
F-statistic: 69.21 on 2 and 29 DF, p-value: 9.109e-12
Step 2: Plot the model
Output:
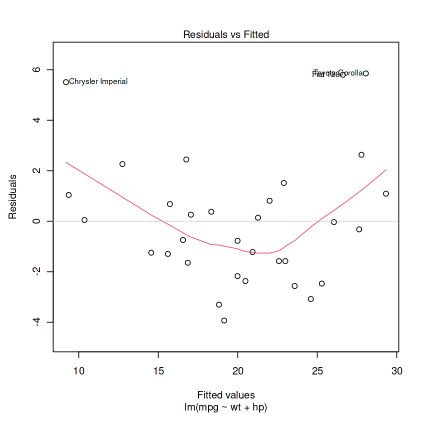
residuals vs fitted values
Above is the scatter plot of the residuals against the fitted values. The plot is used to check for the presence of nonlinearity in the model.

Normal Q-Q plot
The Normal Q-Q plot checks for the assumption of normality by comparing the distribution of the residuals to a normal distribution.
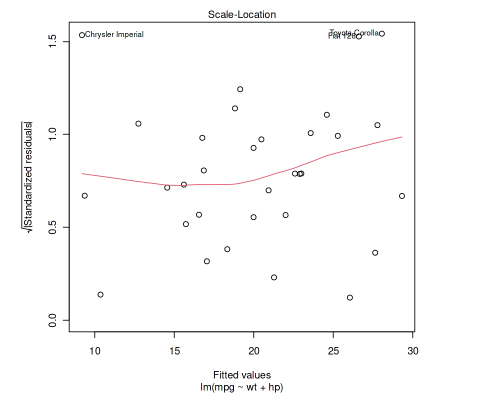
Scale-Location
The above is a plot of the square root of the absolute values of the standardized residuals against the fitted values. It is used to check for the presence of heteroscedasticity (unequal variances of the residuals). If it shows a horizontal line with equally spread points, then it suggests that the residuals have equal variance across the range of fitted values.

Residual vs Leverage
Above is the plot of the standardized residuals against the leverage of each observation. The leverage is a measure of how much an observation affects the regression line. The plot is used to identify influential observations, which are observations that have a high leverage and a large standardized residual. Influential observations can have a significant impact on the regression results and should be examined more closely.
Step 3: Plot the model
Output:
Test stat Pr(>|Test stat|)
wt 3.1383 0.0039785 **
hp 2.4973 0.0186653 *
Tukey test 3.7968 0.0001466 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Pearson Residual for wt, hp, and Fitted values
Example 3: Anova and diagnostic Plots
Step 1: Perform ANOVA on the model
R
library(car)
model <- lm(mpg ~ wt + hp, data = mtcars)
anova(model)
|
Output:
A anova: 3 × 5
Df Sum Sq Mean Sq F value Pr(>F)
<int> <dbl> <dbl> <dbl> <dbl>
wt 1 847.72525 847.725250 126.04109 4.488360e-12
hp 1 83.27418 83.274183 12.38133 1.451229e-03
Residuals 29 195.04775 6.725785 NA NA
The ANOVA function in the above example performs an analysis of variance (ANOVA) on the model that tests the significance of the overall model and the individual variables in the model.
Step 2: Plot partial regression plots for the variables in the model
The plot function creates four plots of the partial regression plots for variables in the model which is useful for understanding the relationship between each variable and the response variable. The partial regression plot shows the relationship between the response variable and each predictor variable which has control for other predictor variables in the model. It allows you to see the unique contribution of each variable to the model and to identify any potential interactions between the variables.
R
par(mfrow=c(2,2))
plot(model, which=c(1,2,3,4,5))
|
Output:
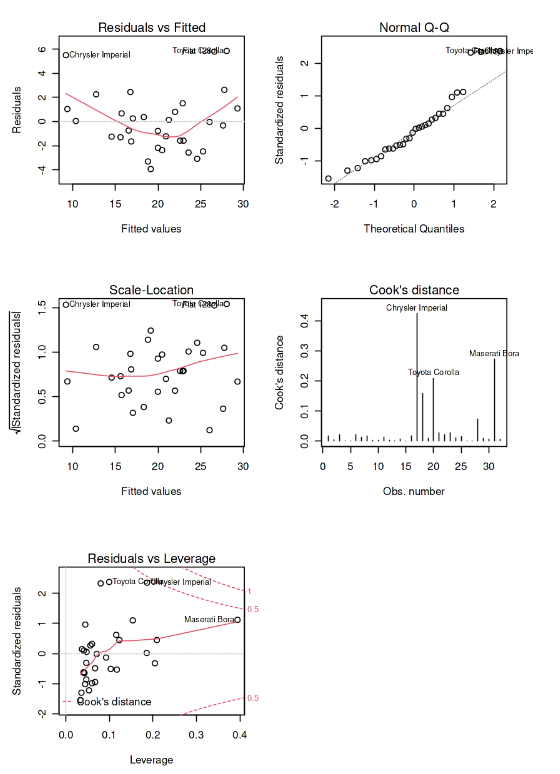
partial regression plots for the variables in the model
The above four diagnostic plots are used to check for the assumptions of linear regression models. The Residuals vs Fitted plot checks for the assumption of linearity by showing the relationship between the residuals and the fitted values. The Normal Q-Q plot checks for the assumption of normality by comparing the distribution of the residuals to a normal distribution. The Scale-Location plot checks for the assumption of homoscedasticity by showing the relationship between the square root of the standardized residuals and the fitted values.
The Cook’s Distance plot checks for influential observations by showing the influence of each observation on the regression coefficients. These plots are important for evaluating the fit of a linear regression model and identifying potential issues, such as outliers or influential observations.
The above shows the influence of each observation on the model fit. Leverage is a measure of how much an observation differs from the average of the predictor variables. It can be used to identify potential influential observations. It suggests a well-fit linear regression model as the points in the plot are randomly distributed, with no points having both high leverage and high residuals.
Conclusion
In conclusion, the car package in R provides a variety of functions and tools for conducting regression analysis and diagnostic plots. In this tutorial, we covered examples of using the car package for regression analysis. By working through the above examples you should now have a good understanding of how to use the car package for regression analysis in R. Whether you’re a beginner or an experienced R user, the car package is a valuable tool for conducting regression analysis and exploring relationships between variables in your data.
Share your thoughts in the comments
Please Login to comment...