Bayes’ Theorem in Data Mining
Last Updated :
04 Jul, 2021
Bayes’ Theorem describes the probability of an event, based on precedent knowledge of conditions which might be related to the event. In other words, Bayes’ Theorem is the add-on of Conditional Probability.
With the help of Conditional Probability, one can find out the probability of X given H, and it is denoted by P(X | H). Now Bayes’ Theorem states that if we know Conditional Probability (P(X | H)) then we can find out P(H | X), given the condition that P(X) and P(H) are already known to us.
Bayes’ Theorem is named after Thomas Bayes. He first makes use of conditional probability to provide an algorithm which uses evidence to calculate limits on an unknown parameter. Bayes’ Theorem has two types of probabilities :
- Prior Probability [P(H)]
- Posterior Probability [P(H/X)]
Where,
- X – X is a data tuple.
- H – H is some Hypothesis.
1. Prior Probability
Prior Probability is the probability of occurring an event before the collection of new data. It is the best logical evaluation of the probability of an outcome which is based on the present knowledge of the event before the inspection is performed.
2. Posterior Probability
When new data or information is collected then the Prior Probability of an event will be revised to produce a more accurate measure of a possible outcome. This revised probability becomes the Posterior Probability and is calculated using Bayes’ theorem. So, the Posterior Probability is the probability of an event X occurring given that event H has occurred.
For example
Suppose, three bags have the labels A, B, and C. One bag has a red ball in it, while the other two do not. The prior probability of red ball found in bag B is one-third or 0.333. But when bag C is seen, and the result shows that there is no red ball in that bag, then the posterior probability of red ball found in bag A and B becomes 0.5, as each bag has one out of two chances.
Formula
Bayes’ Theorem, can be mathematically represented by the equation given below :
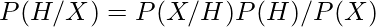
Where,
- H and X are the events and,
- P (X) ≠ 0
- P(H/X) – Conditional probability of H.
Given that X occurs.
- P(X/H) – Conditional probability of X.
Given that H occurs.
- P(H) and P(X) – Prior Probabilities of occurring H and X independent of each other.
This is called the marginal probability.
Formula Derivation of Bayes’ Theorem
According to conditional probability, we know that
P(X|H) = P(X and H)/P(H)
Therefore,
P(X and H) = P(X|H) * P(H) ---------- [1]
Similarly,
P(H|X) = P(H and X)/P(X)
= P(X and H)/P(X) [Order does not matter in Joint Probability]
Therefore,
P(X and H) = P(H|X) * P(X) --------- [2]
Now from equation [1] and [2],
P(X|H) * P(H) = P(H|X) * P(X)
⇒ P(X|H) = P(H|X) * P(X)/P(H)
It means that if we know P(X|H), then we can find out P(H | X),
given the condition that P(X) and P(H) are already known to us.
Now, let us consider X1, X2, X3…..Xk be a group of events having probability P(Xi), i = 1, 2, 3…..k and for any event H where P(H) > 0.
P(Xi|H) = P(Xi and H) / P(H)
= P(H|Xi)*P(Xi) / ∑[P(H|Xi)*P(Xi)

Tree representation of Bayes’ Theorem
To find Reverse Probabilities : Bayes' Theorem
P(X1|H) = P(H|X1)*P(X1) / P(H)
Where
- P(X1) and P(H) are called marginal probabilities.
- P(X1) and P(H|X1) is already given.
Therefore, P(H) can be calculated as given below :
P(H) = P(H|X1)*P(X1) + P(H|X2)*P(X2) + P(H|X3)*P(X3)
(This is also known as Total Probability)To find Reverse Probabilities : Bayes' Theorem
P(X1|H') = P(H'|X1)*P(X1) / P(H')
Now, P(H) can be calculated as
P(H') = P(H'|X1)*P(X1) + P(H'|X2)*P(X2) + P(H'|X3)*P(X3)
Applications of Bayes’ Theorem
In the real world, there are plenty of applications of the Bayes’ Theorem. Some applications are given below :
- It can also be used as a building block and starting point for more complex methodologies, For example, The popular Bayesian networks.
- Used in classification problems and other probability-related questions.
- Bayesian inference, a particular approach to statistical inference.
- In genetics, Bayes’ theorem can be used to calculate the probability of an individual having a specific genotype.
Examples
1. SpamAssassin works as a mail filter to identify the spam in which users train the system. In emails, it considers patterns in the words which are marked as spam by the users. For Example, it may have learned that the word “release” is marked as spam in 30% of the emails. Concluding 0.8% of non-spam mails which includes the word “release” and 40% of all emails which are received by the user is spam. Find the probability that a mail is a spam if the word “release” seems in it.
Solution :
Given,
P(Release | Spam) = 0.30
P(Release | Non Spam) = 0.008
P(Spam) = 0.40
=> P(Non Spam) = 0.40
P(Spam | Release) = ?
Now, using Bayes’ Theorem:
P(Spam | Release) = P(Release | Spam) * P(Spam) / P(Release)
= 0.30 * 0.40 / (0.40 * 0.30 + 0.30 * 0.008)
= 0.980
Hence, the required probability is 0.980.2. Bag1 contains 4 white and 8 black balls and Bag2 contains 5 white and 3 black balls. From one of the bag one ball is drawn at random and the ball which is drawn comes out as black. Find the probability that the ball is drawn from Bag1.
Solution:
Given,
Let E1, E2 and A be the three events where,
E1 = Event of selecting Bag1
E2 = Event of selecting Bag2
A = Event of drawing black ball
Now,
P(E1) = P(E2) = 1/2
P(drawing a black ball from Bag1) = P(A|E1) = 8/12 = 2/3
P(drawing a black ball from Bag2) = P(A|E2) = 3/8
By using Bayes' Theorem, the probability of drawing a black ball from Bag1,
P(E1|A) = P(A|E1) * P(E1) / P(A|E1) * P(E1) + P(A|E2) * P(E2)
[P(A|E1) * P(E1) + P(A|E2) * P(E2) = Total Probability]
= (2/3 * 1/2) / (2/3 * 1/2 + 3/8 * 1/2)
= 16/25
Hence, the probability that the ball is drawn from Bag1 is 16/25
Share your thoughts in the comments
Please Login to comment...