Basic Laws for Various Arithmetic Operations
Last Updated :
14 Apr, 2020
Prerequisite – Number System
A number is a way to represent arithmetic value, count or measure of a particular quantity. A number system can be considered as a mathematical notation of numbers using a set of digits or symbols. In simpler words the number system is a method of representing numbers. Every number system is identified with the help of its base or radix.
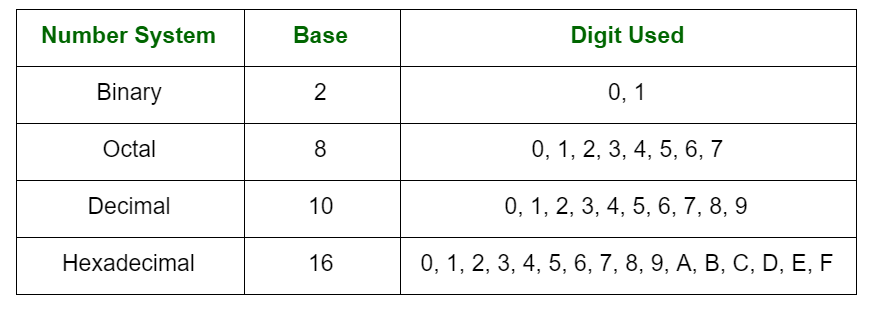
Arithmetic operations like addition, subtraction, multiplication and division are performed in various radix bases. These arithmetic operations may also use r’s complement and (r-1)’s complement representation.
Basic Laws for Various Arithmetic Operations :
These representation techniques hold basic laws for various arithmetic operations:
- Unique Existence law :
The sum and product of any two numbers exist uniquely. We should also note that 0 is the identity element for addition and 1 is the identity element for multiplication.
- Associative law :
Addition and multiplication of binary numbers are associative.
- Commutative law :
Addition and multiplication of binary numbers are commutative.
- Distributive law :
Multiplication of binary numbers is distributive over two or more terms in addition.
Share your thoughts in the comments
Please Login to comment...