Classification of Number System
Last Updated :
28 Jan, 2020
A number is a way to represent arithmetic value, count or measure of a particular quantity. A
number system can be considered as a mathematical notation of numbers using a set of digits or symbols. In simpler words the number system is a method of representing numbers. Every number system is identified with the help of its base or radix.
Base or Radix of a Number System:
The base or radix of a number system can be referred as the total number of different symbols which can be used in a particular number system. Radix means “root” in Latin.
Base equals to 4 implies there are 4 different symbols in that number system. Similarly, base equals to “x” implies there are “x” different symbols in that number system.
Classification of Number System:
The number system can be classified in to two types namely:
Positional and Non-Positional number system
 1. Positional (or Weighted) Number System:
1. Positional (or Weighted) Number System:
A positional number system is also known as weighted number system. As the name implies there will be a weight associated with each digit.
According to its position of occurrence in the number, each digit is weighted. Towards the left the weights increases by a constant factor equivalent to the base or radix. With the help of the radix point (‘.’), the positions corresponding to integral weights (1) are differentiated from the positions corresponding to fractional weights (<1).
Any integer value that is greater than or equal to two can be used as the base or radix. The digit position ‘n’ has weight
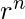
. Largest value of digit position is always 1 less than the base value. The value of a number is weighted sum of its digits.
For example:
1358 = 1 x 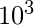 + 3 x
+ 3 x 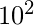 + 5 x
+ 5 x 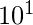 + 8 x
+ 8 x 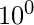 13.58 = 1 x
13.58 = 1 x 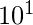 + 3 x
+ 3 x 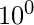 + 5 x
+ 5 x 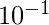 + 8 x
+ 8 x 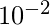
Few examples of positional number system are decimal number system, Binary number system, octal number system, hexadecimal number system, BCD, etc.
2. Non-Positional (or Non-weighted) Number System:
Non-positional number system is also known as non-weighted number system. Digit value is independent of its position. Non-positional number system is used for shift position encodes and error detecting purpose.
Few examples of non-weighted number system are gray code, roman code, excess-3 code, etc.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...