Arithmetic Operations are the basic mathematical operations used for calculation. Arithmetic Operations are the backbone of Mathematics. There are four basic arithmetic operations, namely, Addition, Subtraction, Multiplication, and Division. These four basic arithmetic operations are very helpful in solving daily life calculations such as sharing biscuits among your friend and sibling, counting the total bill you have to pay at a shop, complex calculations such as problems of time and work, data interpretations, etc.
In this article, we will learn about basic arithmetic operations in detail.
What is Arithmetic Operation?
Arithmetic Operation is a set of four fundamental mathematical operations consisting of addition, subtraction, multiplication, and division to solve calculations right from basics to advanced. Arithmetic Operations are used to get a definite value using the four mathematical operations. The term Arithmetic originated from the Greek word “arithmos” which simply means numbers. Hence, Arithmetic is the elementary branch of mathematics that specifically deals with the study of numbers and properties of traditional operations like addition, subtraction, multiplication, and division.
History of Arithmetic
The 17th-century Indian mathematician Brahmagupta is the “father of arithmetic”. Carl Friedrich Gauss in 1801, provided the Fundamental principle of number theory.
Basic Arithmetic Operations
There are four basic mathematical operations that we study in a detailed manner. We can perform these four arithmetic operations for any kind of number including fractions, rational numbers, and complex numbers. These basic mathematical operations are mentioned below:
- Addition
- Subtraction
- Multiplication
- Division
These four arithmetic operations is basically carried out among digits of the number.

Addition Definition
Addition is simply totalling up or summing up two or more numbers to obtain a single value. When we combine two or more numbers or quantities we say are adding. The addition is represented by plus ‘+’ symbol and it is helpful in totalling the bill at a shop, the amount of money you received from different sources, the amount you spend at different places, and in the counting of numbers or quantities. In the counting of numbers, the next number is obtained by adding 1 to the previous number. We can say that Addition is the backbone of counting. Let’s learn some properties of addition.
Properties of Addition
There are the following properties of Addition
- Adding 1 to any number results in the number which is called Successor of the previous number. For Example 8 + 1 = 9, here 9 is the successor of 8.
- Adding 0 to any number results in the number itself. This property is called Additive Identity. For Example 15 + 0 = 15.
- Adding any number with its negative gives zero. The number which is added to result in zero is called Additive Inverse. For Example, 4 + (-4) = 4 – 4 = 0. Here, -4 is the additive inverse of 4.
Subtraction Definition
Subtraction is the method of finding the difference between two numbers. Subtraction is represented by the (-) symbol. Subtraction is the reverse of Addition. Subtraction is useful when you need to calculate how much you will get back after you gave an amount larger than your bill to the shopkeeper, how much a number is larger or smaller than a given number and how much is your monthly saving after summing up all your expenditures. There are two numbers involved in subtraction one is called Minuend, the other one is called Subtrahend and the result obtained on subtraction is called the Difference.
What is Minuend?
The number from which a number is subtracted is called the Minuend. For Example in 7 – 2 = 5, 7 is the Minuend.
What is Subtrahend?
The number which is subtracted is called the Subtrahend. For Example in 7 – 2 = 5, 2 is the subtrahend. If the subtrahend is greater than minuend then the result will be the difference accompanied by a minus sign. For example, in 2 – 7 = -5, here, the numbers are the same but interchanged i.e. subtrahend is 7 and minuend is 2. Here, Subtrahend (7) is greater than minuend(2), hence, the result is also the same i.e. 5 accompanied with a minus sign. Hence, the final result is -5.
What is Difference?
The number obtained by subtraction is called the Difference. For Example in 7 – 2 = 5, the difference is 5. The difference between the two numbers tells us about the gap between two numbers while counting. For example, the difference between 7 and 2 is 5 which tells us that there is a gap of 5 between 7 and 2. The difference between the two numbers also tells how larger or smaller are the two numbers with respect to each other. For Example, in 7 – 2 = 5, we can say that 7 is 5 larger than 2 or 2 is 5 smaller than 7.
Let’s learn some properties of Subtraction
Properties of Subtraction
- Subtracting 1 from any number gives its Predecessor. A Predecessor is a number that occupies place just before a given number in the counting. For Example, 4 – 1 = 3, where 3 is the predecessor of 4.
- Subtracting 0 from any number results in the number itself. For Example, 5 – 0 = 5.
- Subtracting the number from itself results in zero. For Example, 5 – 5 = 0
Multiplication Definition
Multiplication is basically the process of addition of a number to itself for a larger number of times. In this case, the addition becomes lengthy, hence we multiply the number by the number of times it was to be added. For Example, 4 + 4 + 4 + 4 + 4 = 20, in this case, we have added 4 with itself 5 times. Now, to condense this long process we can write it as 4 ⨯ 5 = 20. This process is called Multiplication. Multiplication is represented by the cross (⨯) symbol. Hence, we can say that Multiplication is Repeated Addition. To keep a strong hold on multiplication for calculation one needs to rigorously memorize the tables. There are three terms involved in multiplication, namely, Multiplier, Multiplicand, and Product. Let’s learn them.
What is Multiplier?
Multiplier is the number that is to be multiplied. For Example, we have to multiply 3 by 2 then we can write it as 3 ⨯ 2 = 6, here 3 is the Multiplier.
What is Multiplicand?
The number by which the multiplier is multiplied is called the Multiplicand. For Example, in 3 ⨯ 2 = 6, 2 is the Multiplicand.
What is Product?
The number obtained as a result of multiplication is called the Product. For Example, in 3 ⨯ 2 = 6, the product is 6. We can interpret product 6 as 6 being twice of 3 or two times of 3. If Multiplier and Multiplicand are interchanged then the product remains the same i.e. 3 ⨯ 2 = 6 and 2 ⨯ 3 = 6.
Let’s learn some properties of Multiplication
- Multiplication of any number with zero gives zero. For Example, 3 ⨯ 0 = 0
- Multiplication of any number with 1 gives the same number. For Example, 3 ⨯ 1 = 3. This property is called Multiplicative Identity.
- Multiplication of any number with its reciprocal gives 1. For Example 3 ⨯ 1/3 = 1
Division Definition
Division is the reverse operation of Multiplication. It is the method of reducing a number by continuous subtraction. Division is represented by the (÷) symbol. For Example, if we divide 8 by 2, i.e. 8 ÷ 2, it means we continuously subtract 8 by 2 until we get a number less than 2. We perform this as
8 – 2 = 6
6 – 2 = 4
4 – 2 = 2
2 – 2 = 0
Here, in the fourth step, we get 0 which is less than two. Now we will stop the process here, and the number of steps involved is 4, hence the result of division is 4. Division has got its application from distributing sweets among your friends equally to calculate the per capita income of a country. Let’s learn about the components of division.
Parts of Division
There are four parts of a division
- Dividend: It is the number that is to be divided.
- Divisor: It is the number that divides the dividend.
- Quotient: It is the number that is obtained as a result after division.
- Remainder: It is the number that is left as extra when the dividend is not completely divided.
We can understand the components with the help of the image attached below:

Properties of Division
- A number divided by 1 results in the number itself.
- A number divided by itself gives 1 as the result.
- The result of the division of any number by zero is not defined.
- If the Remainder is zero then the dividend is the multiple of the divisor and the divisor is the factor of the dividend.
Learn More, Long Division Method.
Mathematical Operations
The four basic arithmetic operations i.e. Addition, Subtraction, Multiplication, and Division are to be studied under Mathematical Operations. In reality, Mathematical Operation is an umbrella term that includes basic arithmetic operations,
In this article, our scope is limited to only basic arithmetic operations. The other operations have been covered in different articles and their links have been attached to their keywords.
Arithmetic Properties
The properties followed by arithmetic operations are listed below:
Closure Property
Closure Property is followed by all four arithmetic operations however their meaning differ for different kinds of numbers.
Commutative Property
Commutative Property is followed by addition and multiplication. Commutative Property of Addition states (a + b) = (b + a) and the Commutative Property of Multiplication states (a ⨯ b) = (b ⨯ a).
Associative Property
Associative Property is followed by addition and multiplication only. Associative Property of Addition states that a + (b + c) = (a + b) + c and the Associative Property of Multiplication states that a ⨯ (b ⨯ c) = (a ⨯ b) ⨯ c.
Distributive Property
Distributive Property is followed by multiplication over addition and subtraction. The distributive property of multiplication over addition is given by a ⨯ (b + c) = a ⨯ b + a ⨯ c and the Distributive Property over Subtraction is given as a ⨯ (b – c) = a ⨯ b – a ⨯ c.
Read more about Distributive Property.
Additive Identity
The property of additive identity states that when zero is added to any number it results in the number itself. Additive Identity is given by a + 0 = a
Multiplicative Identity
The property of multiplicative identity states that if any number is multiplied by 1 its results in the number itself.
Additive Inverse
The property of additive inverse states that if a number is added with the negative of itself, the sum is zero. It is expressed as a + (-a) = 0.
Learn more about Additive and Multiplicative Inverse.
Multiplicative Inverse
The property of multiplicative inverse states that if a number is multiplied by its reciprocal, the result is 1. It is expressed as a ⨯ 1/a = 1.
Arithmetic Properties
Let a, b be two integers.
Property
| Addition
| Subtraction
| Multiplication
| Division
|
|---|
Closure Property
| a + b 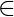 Z Z
| a – b 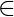 Z Z
| a ⨯ b 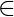 Z Z
| a / b Z Z
|
|---|
Commutative Property
| (a + b) = (b + a)
| (a-b) (b-a) (b-a)
| (a ⨯ b) = (b ⨯ a)
| (a/b) (b/a) (b/a)
|
|---|
Associative Property
| a + (b + c) = (a + b) + c
| a -(b – c)  (a – b) – c (a – b) – c
| a ⨯ (b ⨯ c) = (a ⨯ b) ⨯ c
| a / (b / c)  (a / b) / c (a / b) / c
|
|---|
Distributive Property
| a ⨯ (b + c) = a ⨯ b + a ⨯ c
| a ⨯ (b – c) = a ⨯ b – a ⨯ c
|
Not applicable
|
Not applicable
|
|---|
Identity
|
a + 0 = 0 + a = a
|
Not applicable
| 1 ⨯ a = a ⨯ 1 = a
|
Not applicable
|
|---|
Inverse
| a + (-a) = 0
| Not applicable
| a ⨯ 1/a = 1
| Not applicable
|
|---|
Read More,
Example of Arithmetic Operations
Example 1. The sum of the two numbers is 100, and their difference is 60. Find the numbers.
Solution:
Let the two numbers be x and y
Now, according to the question
x + y = 100 . . . (i)
x – y = 60 . . . (ii)
From equation (i)
⇒ x = 100 – y
Therefore, putting the value of x
⇒ 100 – y – y = 60
⇒ 100 – 2y = 60
⇒ 2y = 40
⇒ y = 20
Putting the value of y in equation (ii)
⇒ x – y = 60
⇒ x = 60 + 20
⇒ x = 80
Therefore, the numbers are 80 and 20 respectively.
Example 2: Simplify 50 + 10(9) – 9
Solution:
50 + 10(9) – 9
⇒ 50 + 90 – 9
⇒ 140 – 9
⇒ 131
Example 3: If the sum of two numbers x and a + 5 is 39. Find the value of x.
Solution:
According to the question,
x + (x + 5) = 39
⇒ 2x + 5 = 39
Subtracting 5 on both sides,
2x + 5 – 5 = 39 – 5
⇒ 2x = 34
x = 34/2 = 17
Therefore, the value of x is 17.
Example 4: The difference between the two numbers is given by finding the value of p.
Solution:
According to the equation,
p – 4 = 11
Adding 4 to the both sides,
p – 4 + 4 = 11 + 4
⇒ p = 15
Therefore, the value of p is 15.
Example 5: Find the value of y in the given equation y – 9 = 3.
Solution:
According to the question,
y – 9 = 3
⇒ y = 9 + 3
⇒ y = 12
Therefore, the value of y is 12.
Example 6: Simplify: -1[(3 – 28) ÷ 5] – 2 × 24 ÷ 6
Solution:
-1[(3 – 28) ÷ 5] – 2 × 24 ÷ 6
⇒ -1 × [(-25) ÷ 5] – 2 × 24 ÷ 6
⇒ -1 × [-5] – 2 × 24 ÷ 6
⇒ 5 – 2 × 24 ÷ 6
⇒ 5 – 48 ÷ 6
⇒ 5 – 8
⇒ -3
Example 7: Solve 2x = 10
Solution:
According to question,
⇒ 2 × x = 10
Dividing both sides with 2
2 × x/2 = 10/2
⇒ x = 5
Therefore, the value of x is 5.
Example 8: Solve the given equation 5x/4 + 1/2 = 2x – 1/2
Solution:
5x/4 + 1/2 = 2x – 1/2
Multiplying both sides with 4
4(5x/4 + 1/2) = 4(2x – 1/2)
⇒ 5x + 2 = 8x – 2
⇒ -3x + 2 = -2
Subtracting both sides with 2
-3x + 2 – 2 = -2 – 2
⇒ x = -4/-3
⇒ x = 4/3
Therefore, the value of x is 4/3.
Example 9: Find the value of the unknown number 3/2y – 2/3 = 1/5y
Solution:
According to the question,
3/2y – 2/3 = 1/5y
Multiplying both sides with 30(LCM of 2, 3, and 5)
30(3/2y – 2/3) = 30(1/5y)
⇒ 45y – 20 = 6y
Adding 20 on both sides,
45y – 20 + 20 = 6y + 20
⇒ 45y = 6y + 20
⇒ 39y = 20
⇒ y = 20/39
Therefore, the value of y is 20/39.
Arithmetic Operations – Practice Problems
Q1. A student purchased a copy for 20 rupees and a pen for 5 rupess then how much money he spend in total?
Q2. There were 5 glasses on a table, 2 of them fall down and got broken. How many unbroken glasses are left?
Q3. In a stack of books there are 10 books, how many books are in total in 3 such stacks?
Q4. John has 20 dollars. He purchased toy worth 4 dollars each. How many toys can he purchase?
Arithmetic Operations-FAQs
1. What are Arithmetic Operations?
Arithmetic Operations are a set of four basic mathematical operations that consist of addition, subtraction, multiplication, and division.
2. What are the Four Arithmetic Operations?
The four Arithmetic Operations are
- Addition
- Subtraction
- Multiplication
- Division
3. Why Arithmetic is Important?
Arithmetic Operations are not only important for solving daily calculations but also complex computational problems.
4. What are Symbols Used in Arithmetic Operations?
The symbols for basic Arithmetic Operations are mentioned below:
- Addition: +
- Subtraction: –
- Multiplication: ⨯
- Division: ÷
5. What is Quotient?
The number obtained by dividing two numbers is called Quotient.
6. What is a Factor?
The number which divides a number completely i.e. the remainder is zero is called a Factor.
7. Who is Known as Father of Arithmetic?
Indian Atronomer and Mathematician Brahamagupta is known as Father of Arithmetic
8. What is BODMAS Rule?
BODMAS Rules explain the order of arithmetic operations that need to be performed in order Bracket, Of, Division, Multiplication, Addition and Subtraction.
Share your thoughts in the comments
Please Login to comment...