Ratio and Proportion are used for comparison in mathematics. Ratio is a comparison of two quantities while Proportion is a comparison of two ratios.
Ratio and proportion are mostly about fractions. When you see a fraction written as a:b, that’s a ratio. A proportion is when two ratios are the same. In both cases, a and b are just any two whole numbers. Understanding ratios and proportions is really important. It helps you grasp many ideas in math and science. Let’s learn about Ratios and Proportions in detail, including their types, formulas, and examples.
Ratio and Proportion Definition
When a fraction a/b is written a:b then it is termed as a ratio b. When two ratios let’s say a:b and c:d are equal a:b and c:d are said to be proportional to each other. Two proportional ratios are written as a:b::c:d.
Ratio Definition
Ratio is a comparison of two quantities of the same unit.
The ratio of two quantities is given by using the colon symbol (:). The ratio of two quantities a and b is given as
a:b
where,
- a is called Antecedent
- b is called Consequent
The ratio a:b means ak/bk where k is the common factor. k is multiplied to give equivalent fractions whose simplest form will be a/b. We can read a:b as ‘a ratio b’ or ‘a to b’.
Ratio Properties
Key properties of Ratio are:
- If a ratio is multiplied by the same term both in antecedent and consequent then there is no change in the actual ratio. For example,
- If the antecedent and consequent of a ratio are divided by the same number then also there is no change in the actual ratio. For Example,
- If two ratios are equal then their reciprocals are also equal i.e. if a:b = c:d then b:a = d:c
- If two ratios are equal then their cross-multiplications are also equal. For Example
- The ratios for a pair of comparisons can be the same but the actual value may be different. For Example, 45:60 = 5:6 and 100:120 = 5:6 hence ratio 5:6 is same but actual value is different
Proportion Definition
Proportion refers to the comparison of ratios. If two ratios are equal then they are said to be proportionate to each other.
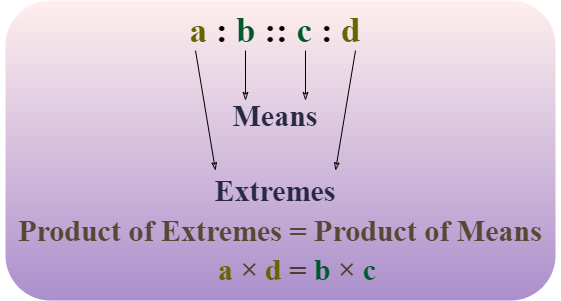
Two proportional ratios are represented by a double colon(::). If two ratios a:b and c:d are equal then they are represented as
a : b :: c : d
where
- a and d are called extreme terms
- b and c are called mean terms
Proportion Properties
Key properties of Proportions are:
- For two ratios in proportion i.e. a/b = c/d, a/c = b/d holds true.
- For two ratios in proportion i.e. a/b = c/d, b/a = d/c holds true.
- For two ratios in proportion i.e. a:b::c:d, the product of mean terms is equal to the product of extreme terms i.e. ad = bc
- For two ratios in proportion i.e. a/b = c/d, (a + b)/b = (c + d)/d is true.
- For two ratios in proportion i.e. a/b = c/d, (a – b)/b = (c – d)/d is true.
Types of Proportions
There are three types of Proportions:
- Direct Proportion
- Inverse Proportion
- Continued Proportion
Let’s learn about them in detail.
Direct Proportion
When two quantities increase and decrease in the same ratio then the two quantities are said to be in Direct Proportion. It means if one quantity increases then the other will also increase and if one will decrease then the other will also decrease.
It is represented as a ∝ b. For Example, Momentum is a product of mass and velocity hence, momentum is directly proportional to mass and velocity (p∝m or p∝v) which means if mass is constant and velocity is high then momentum will also be high and if velocity is constant then momentum will increase with an increase in mass.
Inverse Proportion
When two quantities are inversely related to each other i.e. increase in one leads to a decrease in the other or a decrease in the other leads to an increase in the first quantity then the two quantities are said to be Inversely Proportional to each other.
For Example, Pressure is given by force divided by area (P = F/A). Here Pressure is inversely related to area which means a decrease in area will lead to an increase in pressure and an increase in area will lead to a decrease in pressure.
Continued Proportion
If the ratio a:b = b:c = c:d, then we see that the consequent of the first ratio is equal to the antecedent of the second ratio, and so on then the a:b:c:d is said to be in continued proportion.
- If the consequent and antecedent are not the same for two ratios then they can be converted into continued proportion by multiplying.
- For Example, in the case of a:b and c:d consequent and antecedent are not same then the continued proportion is given as ac:cb:bd.
- In the continued proportion a:b:c:d., c is called the third proportion, and d is called the fourth proportion.
Check: Ratio and Proportion
Let’s discuss the formulas on ratio and proportion in detail.
Ratio Formulas
The ratio of any two quantities a:b is given by a/b where a/b must be in simplest form. In case, you are not able to find the common factor between a and b then find the HCF or a and b and divide a and b with HCF to reduce it to the simplest form.
There are more formulas that we will discuss below:
Compound Ratios
When two ratios are multiplied then the new ratio is called the compound ratio. For example a:b and c:d are two ratios then ac:bd is a compound ratio.
Duplicate Ratios
For a:b, a2:b2 is called duplicate ratios
For a:b, √a:√b is called sub-duplicate ratios
For a:b, a3:b3 is called triplicate ratios
Proportion Formulas
These are the formulas used to solve problems of proportion:
- If a:b = c:d, then we can say that (a + c):(b + d), it is also called Addendo.
- If a:b = c:d, then we can say that (a – c):(b – d), it is also called Subtrahendo.
- If a:b = c:d, then we can say that (a – b):b = (c – d):d, it is also known as Dividendo.
- If a:b = c:d, then we can say that (a + b):b = (c + d):d, it is also known as Componendo.
- If a:b = c:d, then we can say that a:c = b:d, it is also known as Alternendo.
- If a:b = c:d, then we can say that b:a = d:c, it is also called Invertendo.
- If a:b = c:d, then we can say that (a + b):(a – b) = (c + d):(c – d), it is also known as Componendo and Dividendo.
- If a is proportional to b, then it means a = kb where k is a constant.
- If a is inversely proportional to b, then a = k/b, where k is a constant.
- Dividing or multiplying a ratio by a certain number gives an equivalent ratio.
Mean Proportion
Consider two ratios a:b = b:c then as per the rule of proportion product of the mean term is equal to the product of extremes, this means b2 = ac, hence b = √ac is called mean proportion.
Difference between Ratio and Proportion
The comparison between Ratio and Proportion is tabulated below:
|
Ratio vs. Proportion
|
|
Ratio
|
Proportion
|
| Ratio is used to compare two quantities of the same unit |
Proportion is used to compare two ratios |
| Ratio is represented using (:), a/b = a:b |
Proportion is represented using (::), a:b = c:d ⇒ a:b::c:d |
| Ratio is an expression |
Proportion is an equation it equates two ratios |
Read More:
Ratio and Proportion Examples
Now let’s solve some questions on the properties of Ratio and Proportion we discussed so far.
Example 1. Is the ratio 5:10 proportional to 1:2?
Solution:
5:10 divided by 5 gives 1:2. Thus, they are same to each other. So we can say that 5:10 is proportional to 1:2.
Example 2. Given a constant k, such that k:5 is proportional to 10:25. Find the value of k.
Solution:
Since k:5 is proportional to 10:25, we can write,
k / 5 = 10 / 25
k = 10/25 × 5 = 2
So, the value of k is 2.
Example 3. Divide 100 into two parts such that they are proportional to 3:5.
Solution:
Let’s the value of two parts are 3k and 5k, where k is a constant.
Since the total sum of two parts is 100, we can write,
3k + 5k = 100
8k = 100
k = 12.5
So, the parts are 3k = 3 × 12.5 = 37.5 and 5k = 5 × 12.5 = 62.5
Example 4. If x2 + 6y2 = 5xy, then find the value of x/y.
Solution:
Given, x2 + 6y2 = 5xy.
Dividing the equation by y2, we get
(x/y)2 + 6 = 5 (x/y)
Let’s x/y = t
So, we can write,
t2 + 6 = 5t
t2 – 5t + 6 = 0
(t – 2)(t – 3) = 0
t = 2 or t = 3
Since, t = x/y, we get
x/y = 2 or x/y = 3
Conclusion of Ratio and Proportion
Ratio and Proportion are fundamental concepts in mathematics that describe the relationship between quantities and their relative sizes. Ratios express the comparison between two quantities, while proportions establish equality between ratios. Understanding ratios and proportions is essential for solving problems involving scaling, mixing ingredients, financial analysis, and many other scenarios.
Ratios and Proportions – FAQs
What is Definition of Ratio?
Ratio is the comparison of two quantities of same units obtained by their division.
What is Definition of Proportion?
When two ratios are equivalent then the ratios are called to be in Proportion.
What is Direct Proportion?
When two quantities increase or decrease in the same ratio then the two quantities are said to be in direct proportion.
What is Continued Proportion?
When the consequent of the first ratio is the antecedent of the second ratio then two ratios are said to be in Proportion. For Example, a:b and b:c are in continued proportion and can be written as a:b:c.
What is Formula of Ratio and Proportion?
The Ratio of two quantities a and b is given by a:b = a/b and the formula for Proportion for two ratios a:b and c:d is a/b = c/d.
Can we Express Ratio In Terms of Fractions?
Yes, ratios can be expressed in terms of fractions. In fact, ratios are a specific type of fraction where two quantities are compared.
Share your thoughts in the comments
Please Login to comment...