Adaline and Madaline Network

An artificial neural network inspired by the human neural system is a network used to process the data which consist of three types of layer i.e input layer, the hidden layer, and the output layer. The basic neural network contains only two layers which are the input and output layers. The layers are connected with the weighted path which is used to find net input data. In this section, we will discuss two basic types of neural networks Adaline which doesn’t have any hidden layer, and Madaline which has one hidden layer.

1. Adaline (Adaptive Linear Neural) :

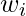
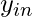• A network with a single linear unit is called Adaline (Adaptive Linear Neural). A unit with a linear activation function is called a linear unit. In Adaline, there is only one output unit and output values are bipolar (+1,-1). Weights between the input unit and output unit are adjustable. It uses the delta rule i.e , where   and 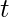 are the weight, predicted output, and true value respectively.
• The learning rule is found to minimize the mean square error between activation and target values. Adaline consists of trainable weights, it compares actual output with calculated output, and based on error training algorithm is applied.

Workflow: 

Adaline

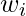
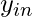First, calculate the net input to your Adaline network then apply the activation function to its output then compare it with the original output if both the equal, then give the output else send an error back to the network and update the weight according to the error which is calculated by the delta learning rule. i.e  , where   and 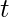 are the weight, predicted output, and true value respectively.

Architecture:

Adaline

In Adaline, all the input neuron is directly connected to the output neuron with the weighted connected path. There is a bias b of activation function 1 is present.

Algorithm: 

      Step 1: Initialize weight not zero but small random values are used. Set learning rate α.

Step 2: While the stopping condition is False do steps 3 to 7.

Step 3: for each training set perform steps 4 to 6.

Step 4: Set activation of input unit x_i = s_i for (i=1 to n).

Step 5: compute net input to output unit

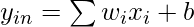
                  Here, b is the bias and n is the total number of neurons.

Step 6: Update the weights and bias for i=1 to n 

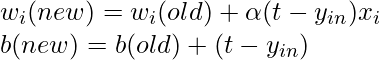
                  and calculate

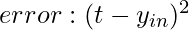
                when the predicted output and the true value are the same then the weight will not change.

Step 7: Test the stopping condition. The stopping condition may be when the weight changes at a low rate or no change.

Implementations

Problem: Design OR gate using Adaline Network?

Solution : 

• Initially, all weights are assumed to be small random values, say 0.1, and set learning rule to 0.1.
• Also, set the least squared error to 2.
• The weights will be updated until the total error is greater than the least squared error.

x1	x2	t
1	1	1
1	-1	1
-1	1	1
-1	-1	-1

• Calculate the net input  

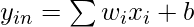
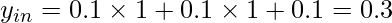        (when x₁=x₂=1)

• Now compute, (t-y_in)=(1-0.3)=0.7
• Now, update the weights and bias

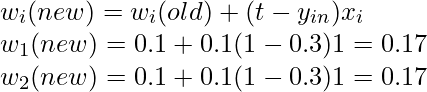
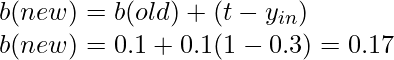
• calculate the error 

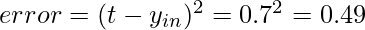
     Similarly, repeat the same steps for other input vectors and you will get.

x1	x2	t	yin	(t-yin)	∆w1	∆w2	∆b	w1 (0.1)	w2 (0.1)	b (0.1)	(t-yin)^2
1	1	1	0.3	0.7	0.07	0.07	0.07	0.17	0.17	0.17	0.49
1	-1	1	0.17	0.83	0.083	-0.083	0.083	0.253	0.087	0.253	0.69
-1	1	1	0.087	0.913	-0.0913	0.0913	0.0913	0.1617	0.1783	0.3443	0.83
-1	-1	-1	0.0043	-1.0043	0.1004	0.1004	-0.1004	0.2621	0.2787	0.2439	1.01

           This is epoch 1 where the total error is 0.49 + 0.69 + 0.83 + 1.01 = 3.02 so more epochs will run until the total error becomes less than equal to the least squared error i.e 2.

Python3

# Import necessary libraries
import numpy as np

#Adaline neural network
def Adaline(Input, Target, lr=0.2, stop=0.001):
    weight = np.random.random(Input.shape[1])
    bias   = np.random.random(1)

    Error=[stop +1]
    # check the stop condition for the network
    while Error[-1] > stop or Error[-1]-Error[-2] > 0.0001:
        error = []
        for i in range(Input.shape[0]):
            Y_input = sum(weight*Input[i]) + bias

            # Update the weight
            for j in range(Input.shape[1]):
                weight[j]=weight[j] + lr*(Target[i]-Y_input)*Input[i][j]

            # Update the bias
            bias=bias + lr*(Target[i]-Y_input)

            # Store squared error value
            error.append((Target[i]-Y_input)**2)
        # Store sum of square errors
        Error.append(sum(error))
        print('Error :',Error[-1])
    return weight, bias

# Input dataset
x = np.array([[1.0, 1.0, 1.0],
              [1.0, -1.0, 1.0],
              [-1.0, 1.0, 1.0],
              [-1.0, -1.0, -1.0]])
# Target values
t = np.array([1, 1, 1, -1])

w,b = Adaline(x, t, lr=0.2, stop=0.001)
print('weight :',w)
print('Bias :',b)

Output:

Error : [2.33228319]
Error : [1.09355784]
Error : [0.73680883]
Error : [0.50913731]
Error : [0.35233593]
Error : [0.24384625]
Error : [0.16876305]
Error : [0.11679891]
Error : [0.08083514]
Error : [0.05594504]
Error : [0.0387189]
Error : [0.02679689]
Error : [0.01854581]
Error : [0.01283534]
Error : [0.00888318]
Error : [0.00614795]
Error : [0.00425492]
Error : [0.00294478]
Error : [0.00203805]
Error : [0.00141051]
Error : [0.0009762]
weight : [0.01081771 0.01081771 0.98675106]
Bias : [0.01081771]

Predictions:

 Predict from the evaluated weight and bias of Adaline

Python3

# Predict from the evaluated weight and bias of adaline
def prediction(X,w,b):
    y=[]
    for i in range(X.shape[0]):
        x = X[i]
        y.append(sum(w*x)+b)
    return y
prediction(x,w,b)

output:

[array([1.0192042]),
 array([0.99756877]),
 array([0.99756877]),
 array([-0.99756877])]

2. Madaline (Multiple Adaptive Linear Neuron) :

• The Madaline(supervised Learning) model consists of many Adaline in parallel with a single output unit. The Adaline layer is present between the input layer and the Madaline layer hence Adaline layer is a hidden layer. The weights between the input layer and the hidden layer are adjusted, and the weight between the hidden layer and the output layer is fixed.
• It may use the majority vote rule, the output would have an answer either true or false. Adaline and Madaline layer neurons have a bias of ‘1’ connected to them. use of multiple Adaline helps counter the problem of non-linear separability.

Architecture:

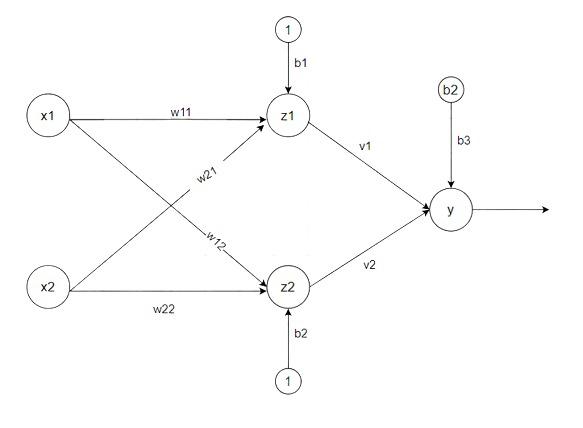
Madaline

      There are three types of a layer present in Madaline First input layer contains all the input neurons, the Second hidden layer consists of an adaline layer, and weights between the input and hidden layers are adjustable and the third layer is the output layer the weights between hidden and output layer is fixed they are not adjustable.

Algorithm:

      Step 1: Initialize weight and set learning rate α.

                     v₁=v₂=0.5  , b=0.5

                 other weight may be a small random value.

Step 2: While the stopping condition is False do steps 3 to 9.

Step 3: for each training set perform steps 4 to 8.

Step 4: Set activation of input unit xi = si for (i=1 to n).

Step 5: compute net input of Adaline unit

                   z_in1 = b₁ + x₁w₁₁ + x₂w₂₁

                   z_in2 = b₂ + x₁w12 + x₂w₂₂

Step 6: for output of remote Adaline unit using activation function given below:

               Activation function f(z) =.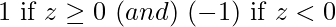

                  z₁=f(z_in1)

                  z₂=f(z_in2)

Step 7: Calculate the net input to output.

                    y_in = b₃ + z₁v₁ + z₂v₂

                   Apply activation to get the output of the net 

                   y=f(y_in)

Step 8: Find the error and do weight updation 

                  if t ≠ y then t=1 update weight on z(j) unit whose next input is close to 0.

                  if t = y no updation

                 w_ij(new) =w_ij(old) + α(t-z_inj)x_i

                 b_j(new) = b_j(old) + α(t-z_inj)

                 if t=-1 then update weights on all unit z_k which have positive net input

Step 9: Test the stopping condition; weights change all number of epochs.

Problem: Using the Madaline network, implement XOR function with bipolar inputs and targets. Assume the required                         parameter for the training of the network.

Solution : 

•  Training pattern for XOR function :

x1	x2	t
1	1	-1
1	-1	1
-1	1	1

• Initially, weights and bias are: Set α = 0.5

                 [w₁₁   w₂₁   b₁] = [0.05    0.2    0.3]

                 [w₁₂   w₂₂   b₂] = [0.1      0.2  0.15]

                 [v₁      v₂     v₃] =   [0.5    0.5    0.5]

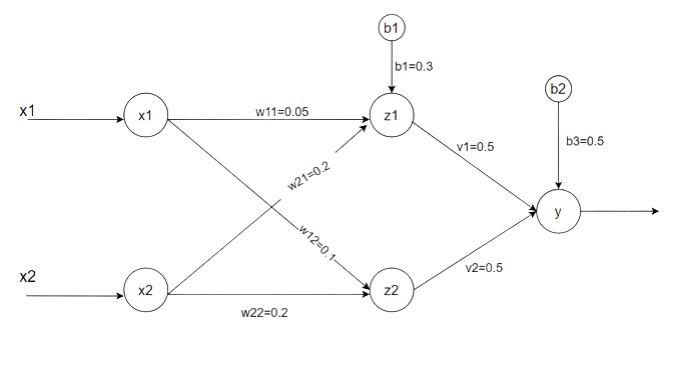
Madaline 

•     for the first i/p & o/p pair from training data :

                   x₁ = 1         x₂ = 1         t = -1         α = 0.5 

•  Net input to the hidden unit :

              z_in1 = b1 + x₁w₁₁ + x₂w₂₁ = 0.05 * 1 + 0.2 *1 + 0.3  = 0.55

              z_in2 = b2 + x₁w₁₂ + x₂w₂₂ = 0.1 * 1 + 0.2 *1 + 0.15  = 0.45

• Apply the activation function f(z) to the net input

                     z₁ = f(z_in1) = f(0.55) = 1

                     z₂ = f(z_in2) = f(0.45) = 1

• computation for the output layer 

                y_in = b3 + z₁v₁ + z₂v₂   = 0.5 + 1 *0.5 + 1*0.5 = 1.5

                y=f(y_in) = f(1.5) = 1

• Since (y=1) is not equal to (t=-1) update the weights and bias 

                w_ij(new) =w_ij(old) + α(t-z_inj)x_i

                b_j(new) = b_j(old) + α(t-z_inj)

•  w₁₁(new) = w₁₁(old) + α(t-z_in1)x₁  = 0.05 + 0.5(-1-0.55) * 1 = -0.725

           w₁₂(new) = w₁₂(old) + α(t-z_in2)x₁  = 0.1 + 0.5(-1-0.45) * 1 = -0.625

           b1(new) = b1(old) +  α(t-z_in1) = 0.3 + 0.5(-1-0.55) = -0.475

           w₂₁(new) = w₂₁(old) + α(t-z_in1)x₂  = 0.2 + 0.5(-1-0.55) * 1 = -0.575

          w₂₂(new) = w₂₂(old) + α(t-z_in2)x₂  = 0.2 + 0.5(-1-0.45) * 1 = -0.525

          b₂(new) = b₂(old) +  α(t-z_in2) = 0.15 + 0.5(-1-0.45) = -0.575

        So, after epoch 1 weight like :

             [w₁₁     w₂₁        b₁] = [-0.725     -0.575     -0.475]

             [w₁₂      w₂₂       b₂] = [-0.625     -0.525       -0.575]

Python3

#Adaline neural network
import numpy as np
import pandas as pd

def activation_fn(z):
    if z>=0:
        return 1
    else:
        return -1

def Madaline(Input, Target, lr, epoch):
    weight = np.random.random((Input.shape[1],Input.shape[1]))
    bias   = np.random.random(Input.shape[1])

    w = np.array([0.5 for i in range(weight.shape[1])])
    b = 0.5
    k = 0
    while k<epoch:
        error = []
        z_input = np.zeros(bias.shape[0])
        z = np.zeros(bias.shape[0])
        for i in range(Input.shape[0]):
            for j in range(Input.shape[1]):
                z_input[j] = sum(weight[j]*Input[i]) + bias[j]
                z[j]= activation_fn(z_input[j])

            y_input = sum(z*w) +b

            y = activation_fn(y_input)
            # Update the weight & bias
            if y != Target[i]:
                for j in range(weight.shape[1]):
                    weight[j]= weight[j] + lr*(Target[i]-z_input[j])*Input[i][j]
                    bias[j]  = bias[j] + lr*(Target[i]-z_input[j])

            # Store squared error value
            error.append((Target[i]-z_input)**2)
        # compute sum of square error
        Error = sum(error)
        print(k,'>> Error :',Error)
        k+=1

    return weight, bias

# Input dataset
x = np.array([[1.0, 1.0, 1.0], [1.0, -1.0, 1.0],
              [-1.0, 1.0, 1.0], [-1.0, -1.0, -1.0]])
# Target values
t = np.array([1, 1, 1, -1])

w,b = Madaline(x, t, 0.0001, 3)
print('weight :',w)
print('Bias :',b)

Output:

0 >> Error : [4.51696958 1.53996419 2.66999799]
1 >> Error : [4.51696958 1.53996419 2.66999799]
2 >> Error : [4.51696958 1.53996419 2.66999799]
weight : [[0.1379015  0.86899587 0.7513866 ]
 [0.82302152 0.19126824 0.35891423]
 [0.52160397 0.1238258  0.88265076]]
Bias : [0.87199879 0.43476458 0.72613887]

Predictions:

 Predict from the evaluated weight and bias of Madaline

Python3

def prediction(X, w,b):
    y =[]
    for i in range(X.shape[0]):
        x = X[i]
        z1 = x*w
        z_1 =[]
        for j in range(z1.shape[1]):
            z_1.append(activation_fn(sum(z1[j])+b[j]))
        y_in = sum(np.array(z_1)*np.array([0.5 for j in range(w.shape[1])])) + 0.5
        y.append(activation_fn(y_in))
    return y

prediction(x, w,b)

Output:

[1, 1, 1, -1]

The output of the Madaline is 100% correct.