Introduction to Artificial Neural Networks | Set 1
Last Updated :
03 Apr, 2024
ANN learning is robust to errors in the training data and has been successfully applied for learning real-valued, discrete-valued, and vector-valued functions containing problems such as interpreting visual scenes, speech recognition, and learning robot control strategies. The study of artificial neural networks (ANNs) has been inspired in part by the observation that biological learning systems are built of very complex webs of interconnected neurons in brains. The human brain contains a densely interconnected network of approximately 10^11-10^12 neurons, each connected neuron, on average connected, to l0^4-10^5 other neurons. So on average human brain takes approximately 10^-1 to make surprisingly complex decisions.
ANN systems are motivated to capture this kind of highly parallel computation based on distributed representations. Generally, ANNs are built out of a densely interconnected set of simple units, where each unit takes a number of real-valued inputs and produces a single real-valued output. But ANNs are less motivated by biological neural systems, there are many complexities to biological neural systems that are not modeled by ANNs.
Difference between Biological Neurons and Artificial Neurons
Biological Neurons
| Artificial Neurons
|
|---|
Major components: Axions, Dendrites, Synapse
| Major components: Axions, Dendrites, Synapse
|
Information from other neurons, in the form of electrical impulses, enters the dendrites at connection points called synapses. The information flows from the dendrites to the cell where it is processed. The output signal, a train of impulses, is then sent down the axon to the synapse of other neurons.
| The arrangements and connections of the neurons made up the network and have three layers. The first layer is called the input layer and is the only layer exposed to external signals. The input layer transmits signals to the neurons in the next layer, which is called a hidden layer. The hidden layer extracts relevant features or patterns from the received signals. Those features or patterns that are considered important are then directed to the output layer, which is the final layer of the network.
|
A synapse is able to increase or decrease the strength of the connection. This is where information is stored.
| The artificial signals can be changed by weights in a manner similar to the physical changes that occur in the synapses.
|
Approx 1011 neurons.
|
102– 104 neurons with current technology
|
Difference between the human brain and computers in terms of how information is processed.
| Human Brain(Biological Neuron Network) | Computers(Artificial Neuron Network) |
|---|
| The human brain works asynchronously | Computers(ANN) work synchronously. |
| Biological Neurons compute slowly (several ms per computation) | Artificial Neurons compute fast (<1 nanosecond per computation) |
| The brain represents information in a distributed way because neurons are unreliable and could die any time. | In computer programs every bit has to function as intended otherwise these programs would crash. |
| Our brain changes their connectivity over time to represents new information and requirements imposed on us. | The connectivity between the electronic components in a computer never change unless we replace its components. |
| Biological neural networks have complicated topologies. | ANNs are often in a tree structure. |
| Researchers are still to find out how the brain actually learns. | ANNs use Gradient Descent for learning. |
Advantage of Using Artificial Neural Networks
- Problem in ANNs can have instances that are represented by many attribute-value pairs.
- ANNs used for problems having the target function output may be discrete-valued, real-valued, or a vector of several real- or discrete-valued attributes.
- ANN learning methods are quite robust to noise in the training data. The training examples may contain errors, which do not affect the final output.
- It is used generally used where the fast evaluation of the learned target function may be required.
- ANNs can bear long training times depending on factors such as the number of weights in the network, the number of training examples considered, and the settings of various learning algorithm parameters.
The McCulloch-Pitts Model of Neuron
- The early model of an artificial neuron is introduced by Warren McCulloch and Walter Pitts in 1943. The McCulloch-Pitts neural model is also known as linear threshold gate.
- These neuron are connected by direct weighted path. The connected path can be excitatory and inhibitory.
- There will be same weight for the excitatory connection entering
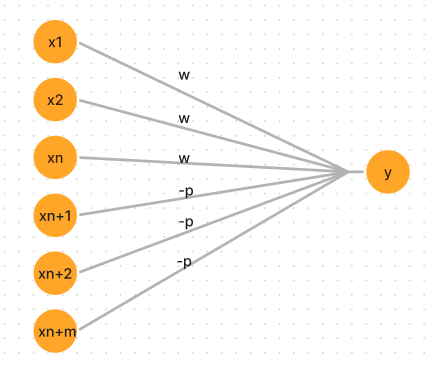
- The connection weights from x1,x2,…….xn are exhibitory denoted by ‘w’ and connection weights from Xn+1 , Xn+2,…….Xn+m are inhibitory denoted by ‘-p’.
-> The McCulloch-Pitts neuron Y has the activation function.
f(yin) = 1 if yin >= Θ where net input yin is given by yin = Σ xiwi
0 if yin < Θ
where Θ is the threshold value and yin is the total net input signal received by neuron Y.
-> The McCulloch-Pitts neuron will fire if it receives k or more exhibitory inputs and no inhibitory inputs.
Kw >= Θ > (K-1)w
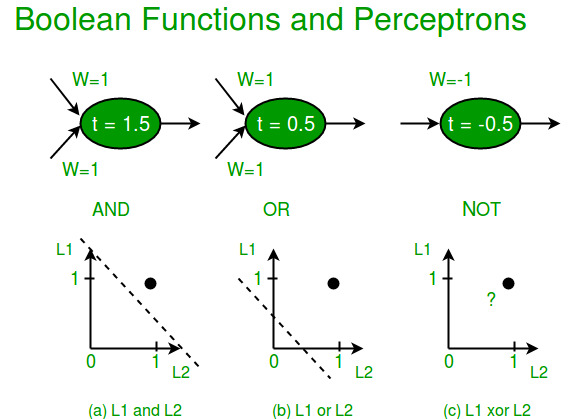
Single-layer Neural Networks (Perceptrons) Input is multi-dimensional (i.e. input can be a vector): input x = ( I1, I2, .., In) Input nodes (or units) are connected (typically fully) to a node (or multiple nodes) in the next layer. A node in the next layer takes a weighted sum of all its inputs: [Tex]\newline Summed Input = \sum_{i}w_iI_i \newline [/Tex]The rule: The output node has a “threshold” t. Rule: If summed input ? t, then it “fires” (output y = 1). Else (summed input < t) it doesn’t fire (output y = 0). [Tex]\newline if \sum_{i}w_iI_i\geqslant t then y=1 \newline else (if \sum_{i}w_iI_i < t) then y=0 \newline [/Tex]which
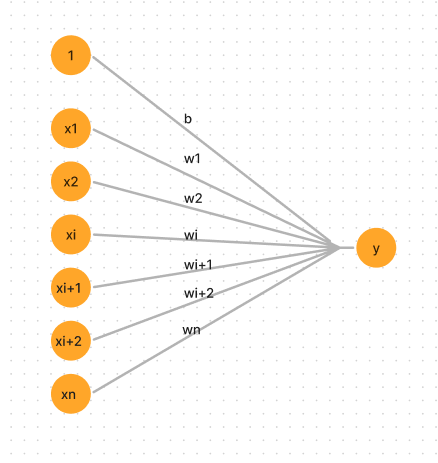
Single layer perceptron
- The input to the response unit will be the output from the associator unit, which is a binary vector.
- The input layer consist of input neurons from x1,x2,………xi……..xn. There always exist a common bias of ‘1’ .
- The input neurons are connected to the output neuron with the weighted interconnection.
Artificial Neural Networks Algorithm
Step 1: Initialize weights and bias. Set learning rate α from (0 to 1).
Step 2: While stopping condition is false repeat steps 3-7.
Step 3: For each training pair do step 4-6.
Step 4: Set activations of input units :
Xi =Sj for 1 to n
Step 5: Compute the output unit response
yin = b + Σ xiwi
The activation function used is :
y=f(yin) = 1 if yin > Θ
0 if -Θ<= yin <= Θ
-1 if yin < -Θ
Step 6: The weights and bias are update if the target is not equal to the output response.
if t ≠ y and the values of xi is not zero
wi(new) = wi(old) + αtxi
b(new) = b(old) + αt
else
wi(new) = wi(old)
b(new) = b(old)
Step 7: Test the stopping condition.
Limitations of Perceptron
- The output values of a perceptron can take on only one of two values (0 or 1) due to the hard-limit transfer function.
- Perceptron can only classify linearly separable sets of vectors. If a straight line or a plane can be drawn to separate the input vectors into their correct categories, the input vectors are linearly separable. If the vectors are not linearly separable, learning will never reach a point where all vectors are classified properly. The Boolean function XOR is not linearly separable (Its positive and negative instances cannot be separated by a line or hyperplane). Hence a single layer perceptron can never compute the XOR function. This is a big drawback that once resulted in the stagnation of the field of neural networks. But this has been solved by multi-layer.
What is Multi-layer Networks?
Multi-layer Neural Networks A Multi-Layer Perceptron (MLP) or Multi-Layer Neural Network contains one or more hidden layers (apart from one input and one output layer). While a single layer perceptron can only learn linear functions, a multi-layer perceptron can also learn non – linear functions. 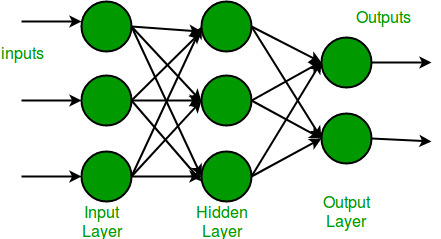 This neuron takes as input x1,x2,….,x3 (and a +1 bias term), and outputs f(summed inputs+bias), where f(.) called the activation function. The main function of Bias is to provide every node with a trainable constant value (in addition to the normal inputs that the node receives). Every activation function (or non-linearity) takes a single number and performs a certain fixed mathematical operation on it. There are several activation functions you may encounter in practice:
This neuron takes as input x1,x2,….,x3 (and a +1 bias term), and outputs f(summed inputs+bias), where f(.) called the activation function. The main function of Bias is to provide every node with a trainable constant value (in addition to the normal inputs that the node receives). Every activation function (or non-linearity) takes a single number and performs a certain fixed mathematical operation on it. There are several activation functions you may encounter in practice:
Sigmoid:takes real-valued input and squashes it to range between 0 and 1. [Tex]\newline \sigma(x) = \frac{1}{(1+exp(-x))} \newline [/Tex]tanh:takes real-valued input and squashes it to the range [-1, 1 ]. [Tex]\newline tanh(x) = 2\sigma( 2x ) -1 \newline [/Tex]ReLu:ReLu stands for Rectified Linear Units. It takes real-valued input and thresholds it to 0 (replaces negative values to 0 ). [Tex]\newline f(x) = max(0,x) \newline [/Tex]
Share your thoughts in the comments
Please Login to comment...