The Stock Span Problem
Last Updated :
22 Nov, 2023
The stock span problem is a financial problem where we have a series of N daily price quotes for a stock and we need to calculate the span of the stock’s price for all N days. The span Si of the stock’s price on a given day i is defined as the maximum number of consecutive days just before the given day, for which the price of the stock on the current day is less than or equal to its price on the given day.
Examples:
Input: N = 7, price[] = [100 80 60 70 60 75 85]
Output: 1 1 1 2 1 4 6
Explanation: Traversing the given input span for 100 will be 1, 80 is smaller than 100 so the span is 1, 60 is smaller than 80 so the span is 1, 70 is greater than 60 so the span is 2 and so on. Hence the output will be 1 1 1 2 1 4 6.
Input: N = 6, price[] = [10 4 5 90 120 80]
Output:1 1 2 4 5 1
Explanation: Traversing the given input span for 10 will be 1, 4 is smaller than 10 so the span will be 1, 5 is greater than 4 so the span will be 2 and so on. Hence, the output will be 1 1 2 4 5 1.
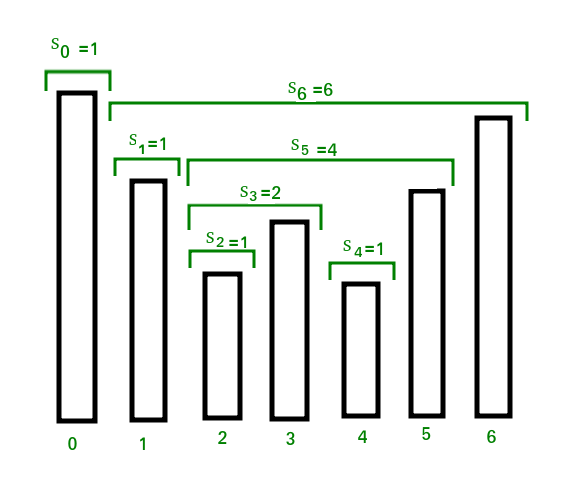
Naive Approach: To solve the problem follow the below idea:
Traverse the input price array. For every element being visited, traverse elements on the left of it and increment the span value of it while elements on the left side are smaller
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void calculateSpan(int price[], int n, int S[])
{
S[0] = 1;
for (int i = 1; i < n; i++) {
S[i] = 1;
for (int j = i - 1;
(j >= 0) && (price[i] >= price[j]); j--)
S[i]++;
}
}
void printArray(int arr[], int n)
{
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
}
int main()
{
int price[] = { 10, 4, 5, 90, 120, 80 };
int n = sizeof(price) / sizeof(price[0]);
int S[n];
calculateSpan(price, n, S);
printArray(S, n);
return 0;
}
|
C
#include <stdio.h>
void calculateSpan(int price[], int n, int S[])
{
S[0] = 1;
for (int i = 1; i < n; i++) {
S[i] = 1;
for (int j = i - 1;
(j >= 0) && (price[i] >= price[j]); j--)
S[i]++;
}
}
void printArray(int arr[], int n)
{
for (int i = 0; i < n; i++)
printf("%d ", arr[i]);
}
int main()
{
int price[] = { 10, 4, 5, 90, 120, 80 };
int n = sizeof(price) / sizeof(price[0]);
int S[n];
calculateSpan(price, n, S);
printArray(S, n);
return 0;
}
|
Java
import java.util.Arrays;
class GFG {
static void calculateSpan(int price[], int n, int S[])
{
S[0] = 1;
for (int i = 1; i < n; i++) {
S[i] = 1;
for (int j = i - 1;
(j >= 0) && (price[i] >= price[j]); j--)
S[i]++;
}
}
static void printArray(int arr[])
{
System.out.print(Arrays.toString(arr));
}
public static void main(String[] args)
{
int price[] = { 10, 4, 5, 90, 120, 80 };
int n = price.length;
int S[] = new int[n];
calculateSpan(price, n, S);
printArray(S);
}
}
|
Python3
def calculateSpan(price, n, S):
S[0] = 1
for i in range(1, n, 1):
S[i] = 1
j = i - 1
while (j >= 0) and (price[i] >= price[j]):
S[i] += 1
j -= 1
def printArray(arr, n):
for i in range(n):
print(arr[i], end=" ")
price = [10, 4, 5, 90, 120, 80]
n = len(price)
S = [None] * n
calculateSpan(price, n, S)
printArray(S, n)
|
C#
using System;
class GFG {
static void calculateSpan(int[] price, int n, int[] S)
{
S[0] = 1;
for (int i = 1; i < n; i++) {
S[i] = 1;
for (int j = i - 1;
(j >= 0) && (price[i] >= price[j]); j--)
S[i]++;
}
}
static void printArray(int[] arr)
{
string result = string.Join(" ", arr);
Console.WriteLine(result);
}
public static void Main()
{
int[] price = { 10, 4, 5, 90, 120, 80 };
int n = price.Length;
int[] S = new int[n];
calculateSpan(price, n, S);
printArray(S);
}
}
|
Javascript
<script>
function calculateSpan(price, n, S)
{
S[0] = 1;
for (let i = 1; i < n; i++) {
S[i] = 1;
for (let j = i - 1; (j >= 0) && (price[i] >= price[j]); j--)
S[i]++;
}
}
function printArray(arr)
{
let result = arr.join(" ");
document.write(result);
}
let price = [ 10, 4, 5, 90, 120, 80 ];
let n = price.length;
let S = new Array(n);
S.fill(0);
calculateSpan(price, n, S);
printArray(S);
</script>
|
PHP
<?php
function calculateSpan($price, $n, $S)
{
$S[0] = 1;
for ($i = 1; $i < $n; $i++)
{
$S[$i] = 1;
for ($j = $i - 1; ($j >= 0) &&
($price[$i] >= $price[$j]); $j--)
$S[$i]++;
}
for ($i = 0; $i < $n; $i++)
echo $S[$i] . " ";;
}
$price = array(10, 4, 5, 90, 120, 80);
$n = count($price);
$S = array($n);
calculateSpan($price, $n, $S);
?>
|
Time Complexity: O(N2)
Auxiliary Space: O(N)
The stock span problem using stack:
To solve the problem follow the below idea:
We see that S[i] on the day i can be easily computed if we know the closest day preceding i, such that the price is greater than on that day than the price on the day i. If such a day exists, let’s call it h(i), otherwise, we define h(i) = -1
The span is now computed as S[i] = i – h(i). See the following diagram

To implement this logic, we use a stack as an abstract data type to store the days i, h(i), h(h(i)), and so on. When we go from day i-1 to i, we pop the days when the price of the stock was less than or equal to price[i] and then push the value of day i back into the stack.
Follow the below steps to solve the problem:
- Create a stack of type int and push 0 in it
- Set the answer of day 1 as 1 and run a for loop to traverse the days
- While the stack is not empty and the price of st.top is less than or equal to the price of the current day, pop out the top value
- Set the answer of the current day as i+1 if the stack is empty else equal to i – st.top
- Push the current day into the stack
- Print the answer using the answer array
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void calculateSpan(int price[], int n, int S[])
{
stack<int> st;
st.push(0);
S[0] = 1;
for (int i = 1; i < n; i++) {
while (!st.empty() && price[st.top()] <= price[i])
st.pop();
S[i] = (st.empty()) ? (i + 1) : (i - st.top());
st.push(i);
}
}
void printArray(int arr[], int n)
{
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
}
int main()
{
int price[] = { 10, 4, 5, 90, 120, 80 };
int n = sizeof(price) / sizeof(price[0]);
int S[n];
calculateSpan(price, n, S);
printArray(S, n);
return 0;
}
|
Java
import java.util.ArrayDeque;
import java.util.Arrays;
import java.util.Deque;
public class GFG {
static void calculateSpan(int price[], int n, int S[])
{
Deque<Integer> st = new ArrayDeque<Integer>();
st.push(0);
S[0] = 1;
for (int i = 1; i < n; i++) {
while (!st.isEmpty()
&& price[st.peek()] <= price[i])
st.pop();
S[i] = (st.isEmpty()) ? (i + 1)
: (i - st.peek());
st.push(i);
}
}
static void printArray(int arr[])
{
System.out.print(Arrays.toString(arr));
}
public static void main(String[] args)
{
int price[] = { 10, 4, 5, 90, 120, 80 };
int n = price.length;
int S[] = new int[n];
calculateSpan(price, n, S);
printArray(S);
}
}
|
Python3
def calculateSpan(price, S):
n = len(price)
st = []
st.append(0)
S[0] = 1
for i in range(1, n):
while(len(st) > 0 and price[st[-1]] <= price[i]):
st.pop()
S[i] = i + 1 if len(st) == 0 else (i - st[-1])
st.append(i)
def printArray(arr, n):
for i in range(0, n):
print(arr[i], end=" ")
price = [10, 4, 5, 90, 120, 80]
S = [0 for i in range(len(price)+1)]
calculateSpan(price, S)
printArray(S, len(price))
|
C#
using System;
using System.Collections;
class GFG {
static void calculateSpan(int[] price, int n, int[] S)
{
Stack st = new Stack();
st.Push(0);
S[0] = 1;
for (int i = 1; i < n; i++) {
while (st.Count > 0
&& price[(int)st.Peek()] <= price[i])
st.Pop();
S[i] = (st.Count == 0) ? (i + 1)
: (i - (int)st.Peek());
st.Push(i);
}
}
static void printArray(int[] arr)
{
for (int i = 0; i < arr.Length; i++)
Console.Write(arr[i] + " ");
}
public static void Main(String[] args)
{
int[] price = { 10, 4, 5, 90, 120, 80 };
int n = price.Length;
int[] S = new int[n];
calculateSpan(price, n, S);
printArray(S);
}
}
|
Javascript
<script>
function calculateSpan(price , n , S)
{
var st = [];
st.push(0);
S[0] = 1;
for (var i = 1; i < n; i++) {
while (st.length!==0 && price[st[st.length - 1]] <= price[i])
st.pop();
S[i] = (st.length===0) ? (i + 1) : (i - st[st.length - 1]);
st.push(i);
}
}
function printArray(arr) {
document.write(arr);
}
var price = [ 10, 4, 5, 90, 120, 80 ];
var n = price.length;
var S = Array(n).fill(0);
calculateSpan(price, n, S);
printArray(S);
</script>
|
Time Complexity: O(N). It seems more than O(N) at first look. If we take a closer look, we can observe that every element of the array is added and removed from the stack at most once.
Auxiliary Space: O(N) in the worst case when all elements are sorted in decreasing order.
To solve the problem follow the below idea:
Since the same subproblems are called again, this problem has the Overlapping Subproblems property. S0, the recomputations of the same subproblems can be avoided by constructing a temporary array to store already calculated answers
- Store the answer for every index in an array and calculate the value of the next index using previous values
- i.e check the answer for previous element and if the value of the current element is greater than the previous element
- Add the answer to the previous index into current answer and then check the value of (previous index – answer of previous index)
- Check this condition repeatedly
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void calculateSpan(int A[], int n, int ans[])
{
ans[0] = 1;
for (int i = 1; i < n; i++) {
int counter = 1;
while ((i - counter) >= 0
&& A[i] >= A[i - counter]) {
counter += ans[i - counter];
}
ans[i] = counter;
}
}
void printArray(int arr[], int n)
{
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
}
int main()
{
int price[] = { 10, 4, 5, 90, 120, 80 };
int n = sizeof(price) / sizeof(price[0]);
int S[n];
calculateSpan(price, n, S);
printArray(S, n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static void calculateSpan(int A[], int n, int ans[])
{
ans[0] = 1;
for (int i = 1; i < n; i++) {
int counter = 1;
while ((i - counter) >= 0
&& A[i] >= A[i - counter]) {
counter += ans[i - counter];
}
ans[i] = counter;
}
}
static void printArray(int arr[], int n)
{
for (int i = 0; i < n; i++)
System.out.print(arr[i] + " ");
}
public static void main(String[] args)
{
int price[] = { 10, 4, 5, 90, 120, 80 };
int n = price.length;
int S[] = new int[n];
calculateSpan(price, n, S);
printArray(S, n);
}
}
|
Python3
def calculateSpan(A, n, ans):
ans[0] = 1
for i in range(1, n):
counter = 1
while ((i - counter) >= 0 and
A[i] >= A[i - counter]):
counter += ans[i - counter]
ans[i] = counter
def printArray(arr, n):
for i in range(n):
print(arr[i], end=' ')
print()
price = [10, 4, 5, 90, 120, 80]
n = len(price)
S = [0] * (n)
calculateSpan(price, n, S)
printArray(S, n)
|
C#
using System;
public class GFG {
static void calculateSpan(int[] A, int n, int[] ans)
{
ans[0] = 1;
for (int i = 1; i < n; i++) {
int counter = 1;
while ((i - counter) >= 0
&& A[i] >= A[i - counter]) {
counter += ans[i - counter];
}
ans[i] = counter;
}
}
static void printArray(int[] arr, int n)
{
for (int i = 0; i < n; i++)
Console.Write(arr[i] + " ");
}
public static void Main(String[] args)
{
int[] price = { 10, 4, 5, 90, 120, 80 };
int n = price.Length;
int[] S = new int[n];
calculateSpan(price, n, S);
printArray(S, n);
}
}
|
Javascript
<script>
function calculateSpan(A, n, ans)
{
ans[0] = 1;
for (let i = 1; i < n; i++) {
let counter = 1;
while ((i - counter) >= 0 && A[i] >= A[i - counter]) {
counter += ans[i - counter];
}
ans[i] = counter;
}
}
function printArray(arr, n) {
for (let i = 0; i < n; i++)
document.write(arr[i] + " ");
}
let price = [10, 4, 5, 90, 120, 80];
let n = price.length;
let S = new Array(n);
calculateSpan(price, n, S);
printArray(S, n);
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(N)
The stock span problem using two stacks:
Follow the below steps to solve the problem:
- In this approach, I have used the data structure stack to implement this task.
- Here, two stacks are used. One stack stores the actual stock prices whereas, the other stack is a temporary stack.
- The stock span problem is solved using only the Push and Pop functions of the Stack.
- Just to take input values, I have taken array ‘price’ and to store output, used array ‘span’.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
vector<int> calculateSpan(int arr[], int n)
{
stack<int> s;
vector<int> ans;
for (int i = 0; i < n; i++) {
while (!s.empty() and arr[s.top()] <= arr[i])
s.pop();
if (s.empty())
ans.push_back(i + 1);
else {
int top = s.top();
ans.push_back(i - top);
}
s.push(i);
}
return ans;
}
void printArray(vector<int> arr)
{
for (int i = 0; i < arr.size(); i++)
cout << arr[i] << " ";
}
int main()
{
int price[] = { 10, 4, 5, 90, 120, 80 };
int n = sizeof(price) / sizeof(price[0]);
int S[n];
vector<int> arr = calculateSpan(price, n);
printArray(arr);
return 0;
}
|
C
#include <limits.h>
#include <stdio.h>
#include <stdlib.h>
#define SIZE 6
typedef int stackentry;
typedef struct stack {
stackentry entry[SIZE];
int top;
} STACK;
void initialiseStack(STACK* s) { s->top = -1; }
int IsStackfull(STACK s)
{
if (s.top == SIZE - 1) {
return (1);
}
return (0);
}
int IsStackempty(STACK s)
{
if (s.top == -1) {
return (1);
}
else {
return (0);
}
}
void push(stackentry d, STACK* s)
{
if (!IsStackfull(*s)) {
s->entry[(s->top) + 1] = d;
s->top = s->top + 1;
}
}
stackentry pop(STACK* s)
{
stackentry ans;
if (!IsStackempty(*s)) {
ans = s->entry[s->top];
s->top = s->top - 1;
}
else {
if (sizeof(stackentry) == 1)
ans = '\0';
else
ans = INT_MIN;
}
return (ans);
}
int main()
{
int price[6] = { 10, 4, 5, 90, 120, 80 };
int span[6] = { 0 };
int i;
STACK s, temp;
initialiseStack(&s);
initialiseStack(&temp);
int count = 1;
span[0] = 1;
push(price[0], &s);
for (i = 1; i < 6; i++) {
count = 1;
while (!IsStackempty(s)
&& s.entry[s.top] <= price[i]) {
push(pop(&s), &temp);
count++;
}
while (!IsStackempty(temp)) {
push(pop(&temp), &s);
}
push(price[i], &s);
span[i] = count;
}
for (i = 0; i < 6; i++)
printf("%d ", span[i]);
}
|
Java
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
class GFG {
static ArrayList<Integer> calculateSpan(int arr[],
int n)
{
Deque<Integer> s = new ArrayDeque<Integer>();
ArrayList<Integer> ans = new ArrayList<Integer>();
for (int i = 0; i < n; i++) {
while (!s.isEmpty() && arr[s.peek()] <= arr[i])
s.pop();
if (s.isEmpty())
ans.add(i + 1);
else {
int top = s.peek();
ans.add(i - top);
}
s.push(i);
}
return ans;
}
static void printArray(ArrayList<Integer> arr)
{
for (int i = 0; i < arr.size(); i++)
System.out.print(arr.get(i) + " ");
}
public static void main(String args[])
{
int price[] = { 10, 4, 5, 90, 120, 80 };
int n = price.length;
ArrayList<Integer> arr = calculateSpan(price, n);
printArray(arr);
}
}
|
Python3
def calculateSpan(a, n):
s = []
ans = []
for i in range(0, n):
while(s != [] and a[s[-1]] <= a[i]):
s.pop()
if(s == []):
ans.append(i+1)
else:
top = s[-1]
ans.append(i - top)
s.append(i)
return ans
def printArray(arr, n):
for i in range(n):
print(arr[i], end=' ')
print()
price = [10, 4, 5, 90, 120, 80]
n = len(price)
ans = calculateSpan(price, n)
printArray(ans, n)
|
C#
using System;
using System.Collections;
using System.Collections.Generic;
class GFG {
public static List<int> calculateSpan(int[] arr, int n)
{
Stack s = new Stack();
List<int> ans = new List<int>();
for (int i = 0; i < n; i++) {
while (s.Count != 0
&& arr[(int)s.Peek()] <= arr[i])
s.Pop();
if (s.Count == 0)
ans.Add(i + 1);
else {
int top = (int)s.Peek();
ans.Add(i - top);
}
s.Push(i);
}
return ans;
}
static void printArray(List<int> arr)
{
for (int i = 0; i < arr.Count; i++)
Console.Write(arr[i] + " ");
}
public static void Main(string[] args)
{
int[] price = { 10, 4, 5, 90, 120, 80 };
int n = price.Length;
List<int> arr = calculateSpan(price, n);
printArray(arr);
}
}
|
Javascript
function calculateSpan(arr, n)
{
let s =[];
let ans=[];
for(let i=0;i<n;i++)
{
while(s.length!=0 && arr[s[s.length-1]] <= arr[i])
s.pop();
if(s.length==0)
ans.push(i+1);
else
{
let top = s[s.length-1];
ans.push(i-top);
}
s.push(i);
}
return ans;
}
let price = [ 10, 4, 5, 90, 120, 80 ];
let n = price.length;
let arr = calculateSpan(price, n);
document.write(arr);
|
Time Complexity: O(N), where N is the size of the array.
Auxiliary Space: O(N), where N is the size of the array.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...