Stack in Python
Last Updated :
14 Mar, 2024
A stack is a linear data structure that stores items in a Last-In/First-Out (LIFO) or First-In/Last-Out (FILO) manner. In stack, a new element is added at one end and an element is removed from that end only. The insert and delete operations are often called push and pop.
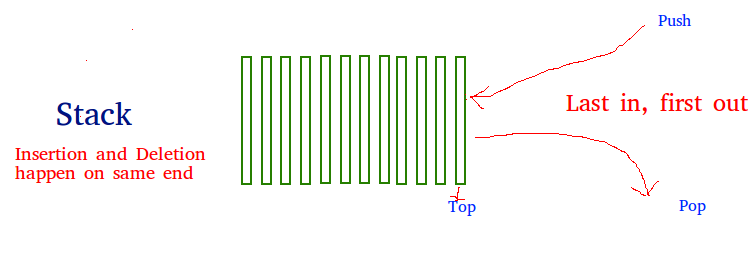
The functions associated with stack are:
- empty() – Returns whether the stack is empty – Time Complexity: O(1)
- size() – Returns the size of the stack – Time Complexity: O(1)
- top() / peek() – Returns a reference to the topmost element of the stack – Time Complexity: O(1)
- push(a) – Inserts the element ‘a’ at the top of the stack – Time Complexity: O(1)
- pop() – Deletes the topmost element of the stack – Time Complexity: O(1)
Implementation:
There are various ways from which a stack can be implemented in Python. This article covers the implementation of a stack using data structures and modules from the Python library.
Stack in Python can be implemented using the following ways:
- list
- Collections.deque
- queue.LifoQueue
Implementation using list:
Python’s built-in data structure list can be used as a stack. Instead of push(), append() is used to add elements to the top of the stack while pop() removes the element in LIFO order.
Unfortunately, the list has a few shortcomings. The biggest issue is that it can run into speed issues as it grows. The items in the list are stored next to each other in memory, if the stack grows bigger than the block of memory that currently holds it, then Python needs to do some memory allocations. This can lead to some append() calls taking much longer than other ones.
Python3
# Python program to
# demonstrate stack implementation
# using list
stack = []
# append() function to push
# element in the stack
stack.append('a')
stack.append('b')
stack.append('c')
print('Initial stack')
print(stack)
# pop() function to pop
# element from stack in
# LIFO order
print('\nElements popped from stack:')
print(stack.pop())
print(stack.pop())
print(stack.pop())
print('\nStack after elements are popped:')
print(stack)
# uncommenting print(stack.pop())
# will cause an IndexError
# as the stack is now empty
OutputInitial stack
['a', 'b', 'c']
Elements popped from stack:
c
b
a
Stack after elements are popped:
[]
Implementation using collections.deque:
Python stack can be implemented using the deque class from the collections module. Deque is preferred over the list in the cases where we need quicker append and pop operations from both the ends of the container, as deque provides an O(1) time complexity for append and pop operations as compared to list which provides O(n) time complexity.
The same methods on deque as seen in the list are used, append() and pop().
Python3
# Python program to
# demonstrate stack implementation
# using collections.deque
from collections import deque
stack = deque()
# append() function to push
# element in the stack
stack.append('a')
stack.append('b')
stack.append('c')
print('Initial stack:')
print(stack)
# pop() function to pop
# element from stack in
# LIFO order
print('\nElements popped from stack:')
print(stack.pop())
print(stack.pop())
print(stack.pop())
print('\nStack after elements are popped:')
print(stack)
# uncommenting print(stack.pop())
# will cause an IndexError
# as the stack is now empty
OutputInitial stack:
deque(['a', 'b', 'c'])
Elements popped from stack:
c
b
a
Stack after elements are popped:
deque([])
Implementation using queue module
Queue module also has a LIFO Queue, which is basically a Stack. Data is inserted into Queue using the put() function and get() takes data out from the Queue.
There are various functions available in this module:
- maxsize – Number of items allowed in the queue.
- empty() – Return True if the queue is empty, False otherwise.
- full() – Return True if there are maxsize items in the queue. If the queue was initialized with maxsize=0 (the default), then full() never returns True.
- get() – Remove and return an item from the queue. If the queue is empty, wait until an item is available.
- get_nowait() – Return an item if one is immediately available, else raise QueueEmpty.
- put(item) – Put an item into the queue. If the queue is full, wait until a free slot is available before adding the item.
- put_nowait(item) – Put an item into the queue without blocking. If no free slot is immediately available, raise QueueFull.
- qsize() – Return the number of items in the queue.
Python3
# Python program to
# demonstrate stack implementation
# using queue module
from queue import LifoQueue
# Initializing a stack
stack = LifoQueue(maxsize=3)
# qsize() show the number of elements
# in the stack
print(stack.qsize())
# put() function to push
# element in the stack
stack.put('a')
stack.put('b')
stack.put('c')
print("Full: ", stack.full())
print("Size: ", stack.qsize())
# get() function to pop
# element from stack in
# LIFO order
print('\nElements popped from the stack')
print(stack.get())
print(stack.get())
print(stack.get())
print("\nEmpty: ", stack.empty())
Output0
Full: True
Size: 3
Elements popped from the stack
c
b
a
Empty: True
Implementation using a singly linked list:
The linked list has two methods addHead(item) and removeHead() that run in constant time. These two methods are suitable to implement a stack.
- getSize()– Get the number of items in the stack.
- isEmpty() – Return True if the stack is empty, False otherwise.
- peek() – Return the top item in the stack. If the stack is empty, raise an exception.
- push(value) – Push a value into the head of the stack.
- pop() – Remove and return a value in the head of the stack. If the stack is empty, raise an exception.
Below is the implementation of the above approach:
Python3
# Python program to demonstrate
# stack implementation using a linked list.
# node class
class Node:
def __init__(self, value):
self.value = value
self.next = None
class Stack:
# Initializing a stack.
# Use a dummy node, which is
# easier for handling edge cases.
def __init__(self):
self.head = Node("head")
self.size = 0
# String representation of the stack
def __str__(self):
cur = self.head.next
out = ""
while cur:
out += str(cur.value) + "->"
cur = cur.next
return out[:-2]
# Get the current size of the stack
def getSize(self):
return self.size
# Check if the stack is empty
def isEmpty(self):
return self.size == 0
# Get the top item of the stack
def peek(self):
# Sanitary check to see if we
# are peeking an empty stack.
if self.isEmpty():
raise Exception("Peeking from an empty stack")
return self.head.next.value
# Push a value into the stack.
def push(self, value):
node = Node(value)
node.next = self.head # Make the new node point to the current head
self.head = node # Update the head to be the new node
self.size += 1
# Remove a value from the stack and return.
def pop(self):
if self.isEmpty():
raise Exception("Popping from an empty stack")
remove = self.head.next
self.head.next = self.head.next.next
self.size -= 1
return remove.value
# Driver Code
if __name__ == "__main__":
stack = Stack()
for i in range(1, 11):
stack.push(i)
print(f"Stack: {stack}")
for _ in range(1, 6):
remove = stack.pop()
print(f"Pop: {remove}")
print(f"Stack: {stack}")
Output
Stack: 10->9->8->7->6->5->4->3->2->1
Pop: 10
Pop: 9
Pop: 8
Pop: 7
Pop: 6
Stack: 5->4->3->2->1
Advantages of Stack:
- Stacks are simple data structures with a well-defined set of operations, which makes them easy to understand and use.
- Stacks are efficient for adding and removing elements, as these operations have a time complexity of O(1).
- In order to reverse the order of elements we use the stack data structure.
- Stacks can be used to implement undo/redo functions in applications.
Drawbacks of Stack:
- Restriction of size in Stack is a drawback and if they are full, you cannot add any more elements to the stack.
- Stacks do not provide fast access to elements other than the top element.
- Stacks do not support efficient searching, as you have to pop elements one by one until you find the element you are looking for.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...