Using Learning Curves – ML
Last Updated :
17 Jul, 2020
A learning model of a Machine Learning model shows how the error in the prediction of a Machine Learning model changes as the size of the training set increases or decreases.
Before we continue, we must first understand what variance and bias mean in the Machine Learning model.
Bias:
It is basically nothing but the difference between the average prediction of a model and the correct value of the prediction. Models with high bias make a lot of assumptions about the training data. This leads to over-simplification of the model and may cause a high error on both the training and testing sets. However, this also makes the model faster to learn and easy to understand. Generally, linear model algorithms like Linear Regression have a high bias.
Variance:
It is the amount a model’s prediction will change if the training data is changed. Ideally, a machine learning model should not vary too much with a change in training sets i.e., the algorithm should be good at picking up important details about the data, regardless of the data itself. Example of algorithms with high variance is Decision Trees, Support Vector Machines (SVM).
Ideally, we would want a model with low variance as well as low bias. To achieve lower bias, we need more training data but with higher training data, the variance of the model will increase. So, we have to strike a balance between the two. This is called the bias-variance trade-off.
A learning curve can help to find the right amount of training data to fit our model with a good bias-variance trade-off. This is why learning curves are so important.
Now that we understand the bias-variance trade-off and why a learning curve is important, we will now learn how to use learning curves in Python using the scikit-learn library of Python.
Implementation of Learning Curves in Python:
For the sake of this example, we will be using the very popular, ‘Digit’ data set. For more information on this data set, you can refer to the link below :https://scikit-learn.org/stable/auto_examples/datasets/plot_digits_last_image
We will use a k-Nearest Neighbour classifier for this example. We will also perform 10-fold cross-validation for obtaining validation scores to plot on the graph.
Code:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_digits
from sklearn.model_selection import learning_curve
dataset = load_digits()
X, y = dataset.data, dataset.target
sizes, training_scores, testing_scores = learning_curve(KNeighborsClassifier(), X, y, cv=10, scoring='accuracy', train_sizes=np.linspace(0.01, 1.0, 50))
mean_training = np.mean(training_scores, axis=1)
Standard_Deviation_training = np.std(training_scores, axis=1)
mean_testing = np.mean(testing_scores, axis=1)
Standard_Deviation_testing = np.std(testing_scores, axis=1)
plt.plot(sizes, mean_training, '--', color="b", label="Training score")
plt.plot(sizes, mean_testing, color="g", label="Cross-validation score")
plt.title("LEARNING CURVE FOR KNN Classifier")
plt.xlabel("Training Set Size"), plt.ylabel("Accuracy Score"), plt.legend(loc="best")
plt.tight_layout()
plt.show()
|
Output:
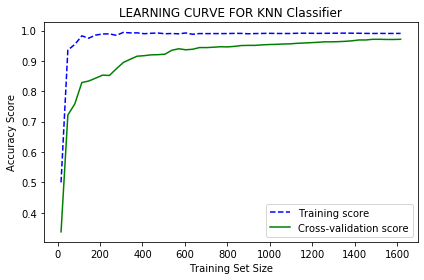
From the curve, we can clearly see that as the size of the training set increases, the training score curve and the cross-validation score curve converge. The cross-validation accuracy increases as we add more training data. So adding training data is useful in this case. Since the training score is very accurate, this indicates low bias and high variance. So this model also begins overfitting the data because the cross-validation score is relatively lower and increases very slowly as the size of the training set increases.
Conclusion:
Learning Curves are a great diagnostic tool to determine bias and variance in a supervised machine learning algorithm. In this article, we have learnt what learning curves and how they are implemented in Python.
Share your thoughts in the comments
Please Login to comment...