Types of Vectors

Vector is a physical quantity that has both direction and magnitude, it is a quantity that not only tells us about its strength but also gives us details about the direction in which it is acting upon. There are various types of vectors based on different parameters like their direction, magnitude, and position. Each type of vector has its own properties and uses. The concept of vector is widely used in physics, mathematics, engineering, and various other fields.

Further in this article, we will discuss in detail various types of vectors one by one, along with numerous solved and unsolved examples based on vectors, but let’s first learn what a vector actually is.

What is a Vector?

A vector is defined a​s a quantity that has both magnitude and direction. The word ‘vector’ is a Latin word that means a ‘carrier’. A vector acts as a carrier from one point to another. The direction of a vector is denoted by ‘→’ which points a vector from its initial point towards its final point. The magnitude of vector is denoted by |x|, where x is the vector. The quantities with both magnitude and direction are known as vector quantities. Displacement, Velocity, and Acceleration are some examples of vector quantities.

Types Of Vectors

Vectors are further classified into various types based on their position, direction and magnitude. It is broadly classified into different types namely:

• Unit Vector
• Orthogonal Vector
• Parallel Vector
• Anti-parallel Vector
• Zero Vectors
• Negative of a Vector
• Equal Vectors
• Collinear Vectors
• coplanar Vectors
• position Vectors
• Displacement Vectors
• Localized Vectors
• Non-localized Vectors
• Co-initial Vectors
• Like and Unlike Vectors

Each type of vector varies in their properties and are helpful in performing numerous operations based on vectors. We will now discuss about each type of vector in detail.

Types of Vectors based on Direction​

Each vector has its properties and is unique in its kind. As one of the vital features of vectors is their direction, based on direction the different types of vectors are-

Unit Vector

If the magnitude of a vector is 1, it is known as a unit vector. It is used to indicate the direction of a vector. It is denoted by ‘^’, which is known as a cap. It is also known as Directional Vector. In the Cartesian plane, i, j, and k are unit vectors along the direction of the x-axis, y-axis, and z-axis respectively.

If x is a unit vector then, |x| =1.

Formula to Find Unit Vector Along any Vector

To find a unit vector in the direction of a vector, we divide the vector by its magnitude.

If is a vector and || is its magnitude then, the unit vector is

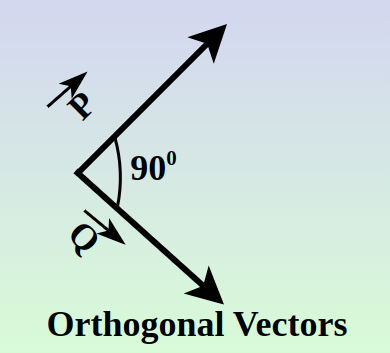
Orthogonal Vector

In mathematics, orthogonal simply means perpendicular and so Orthogonal vector also means perpendicular vectors, i.e. two vectors are said to be orthogonal if they are perpendicular to each other. Also in other words two vectors are orthogonal if there dot product is 0 (zero).

For example, if then P and Q are orthogonal vectors.

Parallel Vector

Two vectors are said to be parallel vectors if they are in the same direction and the angle between them is 0°. They are also called Collinear-vectors. These vectors never intersect each other.
In parallel vectors the distance between them is always constant i.e. the distance between them never changes.

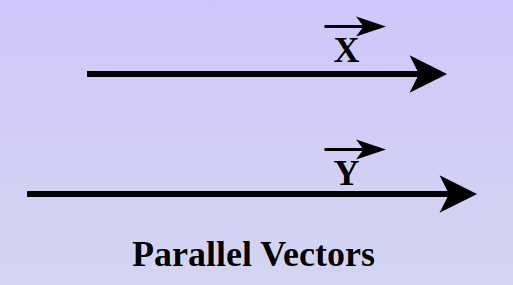
Some properties of parallel vectors:

• The cross product of two parallel vectors is always 0.
• The dot product of two parallel vectors x and y is equal to |x| |y|.
• Two vectors x and y, are only parallel if x = ay, where ‘a’ is scalar.

Anti-Parallel Vector

Two vectors are said to be Anti-parallel vectors if they are in exactly opposite directions and the angle between them is 180°. They are the opposite of parallel vectors in terms of the direction. If ‘x’ is a vector, then ‘-x’ is its anti-parallel vector.

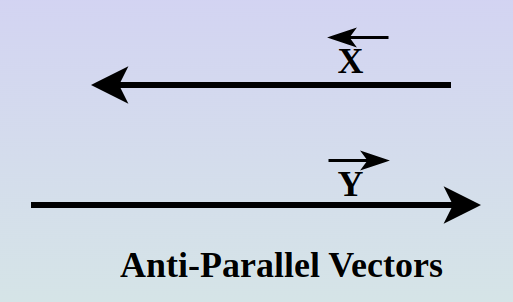
Some properties of anti-parallel vectors:

• The cross product of two anti-parallel vectors is always 0.
• The dot product of two anti-parallel vectors x and y is equal to – |x| |y|.
• Two vectors x and y, are only anti-parallel if x = ay, where ‘a’ is non scalar.

Zero Vector

In a zero vector, the magnitude of the vector is always 0 and its direction is not defined, i.e. it points nowhere. It is also known as a null vector. All the components of these vectors are 0 always.

In cartesian plane a zero vector, = (0,0,0)

Negative of a Vector

A negative of a vector means the vector is in exactly the opposite direction of that vector. The magnitude of the negative vectors always remains the same but the direction is reversed.

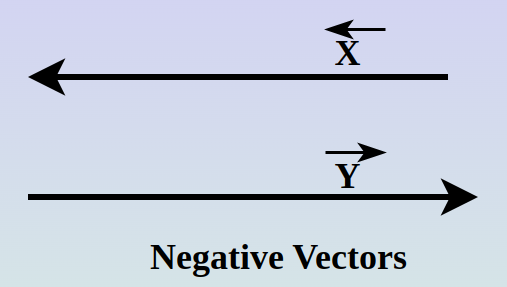
If y is a negative vector of x then:

• y = -x
• |y| = |x|

Types of Vectors Based on Magnitude

Based on the magnitude, the vectors are mainly classified into 3 types namely:

Equal Vectors

If both the direction and magnitude of two or more vectors are exactly the same, then they are known as equal vectors. The starting point of equal vectors can be different but their magnitude and direction should be the same.

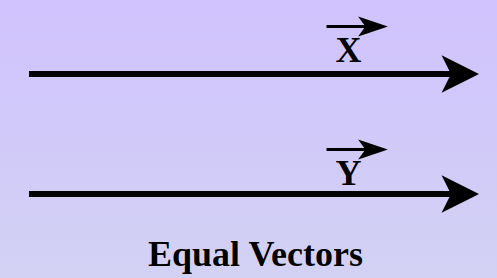
The cartesian coordinates of equal vectors are also the same. If a(x_{1 ,} y₁) is equal to b(x₂ , y₂) then:

x₁ = x₂

y₁ = y₂

Collinear Vectors

Vectors are said to be Collinear Vectors if they lie on the same line or are parallel to the same line. They are also known as parallel vectors. All parallel and antiparallel vectors are collinear vectors.

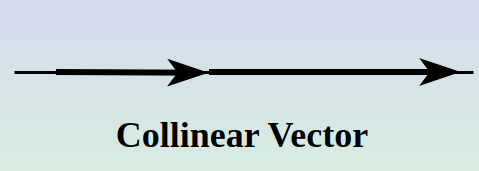
Some properties of collinear vectors:

• The cross product of two collinear vectors is always 0.
• Two vectors x and y, are collinear only if x = ay, where ‘a’ is scalar.
• In collinear vectors, the relation of their coordinates are equal, i.e. x₁ / x₂ = y₁ / y₂ = z₁ / z₂ , with a condition that each component is non-zero.

Coplanar Vectors

A set of vectors is said to be Coplanar vectors if they lie on the same plane. These vectors can be perpendicular to each other, can be parallel, or can be any random vector on the same plane.

Three vectors are said to be Coplanar Vectors, if their scalar triple product is zero.

Types of Vectors Based on Position

Based on the position, the different types of vectors are Position Vectors, Displacement Vectors, Localized Vectors and Non-Localized Vectors.

Position Vectors

The position vector represents the position of an object in a space relative to a reference position, which is the origin in general. These vectors point towards the location of a vector in the cartesian plane. The position vector has a fixed point which is the reference point, from here it points towards the position of the vector in space. It has a magnitude as well as a direction.

The position vectors are represented by the coordinates pair. It is denoted by ‘‘. It can be derived by using the formula:

If XY is a position vector with its reference position (X) at the origin and the coordinates of Y are (x,y,z), then it is represented as:

Displacement Vectors

If a vector moves from point A to point B then its change in position along the particular direction (that provides the least distance between A and B) is given by displacement vector. A displacement vector describes the change in location of a moving object along the least distance (magnitude) between its initial and its final position.

To find the displacement vector between point A and point B, we find the difference between position vectors at A and B.

For example if, = 3i + 2j + 7k and = 4i + j + 5k, then the displacement vector from A to B will be:

= i – j – 2k

where and are position vectors at A and B respectively.

Localized Vector

Localized vectors ( also known as Fixed vectors) are those vectors in which either the initial or final position is fixed. The term localized here simply means a specific location or position in space. They represent quantities related to specific positions, for example, displacement and force. A vector drawn parallel to a given vector with a specific position is also known as a localized vector.

Non-Localized or Free Vector

Non-localized or Free vectors have fixed magnitude and direction but are not tied to a particular position. They do not have any fixed position and are free in space. They can be applied to any arbitrary point in space without changing its properties. These vectors are independent of their position and can be applied anywhere. Velocity and momentum are examples of non-localized vectors.

Some other Types of Vectors

Apart from above classified vectors there exists some other types of vectors which are discussed below:

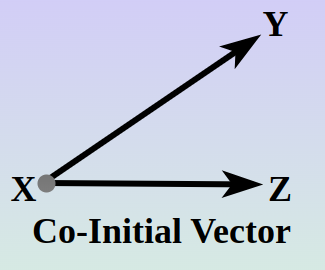
Co-Initial Vectors

Co-initial vectors refer to the vectors that have a common initial point. In simple words, two or more vectors are said to be co-initial vectors, if their starting point is the same.

XY and XZ are Co-Initial vectors with the same starting point X.

Like and Unlike Vectors

Like and unlike vectors depend on the direction of the other vector. If two or more vectors are in the same direction then they are said to be like vectors. But if the vectors are in opposite directions they are said to be unlike vectors.

Solved Problems on Types of Vectors

Example 1: Find the magnitude of a vector A= i + 4j – 2k.

Solution:

We know the magnitude of a vector A, can be given by using the formula: | A | = √x² + y² + z²

Given, A = i + 4j – 2k

Hence here, x = 1 , y = 4 and z= -2

Inserting the values in the formula we get,

| A | = √1² + 4² + (-2)²

⇒ | A | = √1 + 16 + 4

⇒ | A | = √21

Hence the magnitude of A = i + 4j – 2k is √21.

Example 2: Find the dot product of A = 3i + 4j and B = 2i + 3j + 2k, Given A and B, are parallel to each other.

Solution:

We know that the dot product of two parallel vectors A and B is equal to |A| |B|.

So, |A| = √3² + 4² + 0²

⇒ |A| = √9+16+0 =√25

⇒ |A| = 5

Also, |B| = √2² + 3² + 2²

|B| = √4+9+4 = √17

We know, A . B = |A| |B|

Putting derived values of |A| and |B|, we get

A.B = 5√17

Hence the dot product of given vectors A and B is 5√17.

Example 3: Find the unit vector of vector a = 2i – 4j + 3k

Solution:

Given vector a = 2i – 4j + 3k

Also, here = √(2)² + (-4)² + (3)²

⇒ = √4 + 16 + 9

⇒ = √29

We know to find a unit vector we use the formula:

Putting values of and , we get:

= (2i – 4j + 3k) / √29

⇒ = 2/√29 i – 4/√29 j + 3/√29 k

Hence the required unit vector is = 2/√29 i – 4/√29 j + 3/√29 k

Example 4: Check whether X(1, 2, -2), Y(-1, 4, -3), and Z(-3, 6, -4) are collinear or not.

Solution:

Given, X(1, 2, -2), Y(-1, 4, -3), Z(5,-2, -3)

⇒ = (-1-1)i + (4-2)j + (-3-(-2)) k

⇒ = -2i + 2j – k

⇒ = (-3-(-1))i + (6-4)j + (-4-(-3))k

⇒ = -2i + 2j – k

⇒ = (1-(-3))i + (2-6)j +(-2-(-4))k

⇒ = 4i – 4j + 2k

Now,

= √(-2)² + (2)² + (-1)²

⇒ = √4 + 4 + 1

⇒ = √9 = 3

⇒ = √(-2)² + (2)² + (-1)²

⇒ = √4 + 4 + 1

⇒ = V9 = 3

⇒ = √(4)² + (-4)² + (2)²

⇒ = √16 + 16 + 4

⇒ = √36 = 6

Also the three points X, Y and Z are collinear if

Putting values we get,

3 + 3 = 6, which is true

Hence, the given points X(1, 2, -2), Y(-1, 4, -3), and Z(-3, 6, -4) are collinear.

Practice Questions on Types of Vectors

Q1: Find the unit vector of P = 3i – 4j + 5k.

Q2: Check if P(1, -1, 0), Q(2, 3, 4), R(1, 0 ,-3) are coplanar or not.

Q3: Find the dot product of vector A = 2i – j + k and vector B = -i +4j -3k, if A and B are anti-parallel vectors.

Q4: Check if P(-1, 2, 0), Q(3, -1, -2), R(6, -3, 1) are collinear or not.

Q5: Find the magnitude of Vector A = 2i -2j +k

Types of Vectors – FAQs

1. How to Calculate the Magnitude of a Vector?

We can calculate the magnitude of a vector by the formula:

| v | = √x² + y² (For 2-D vectors)

| v | = √x² + y² + z²(For 3-D vectors)

2. What are the Vector Formulas?

To perform operation on vectors, various formulas used few of them are:

• 
• 
• 

3. What is the Difference between Distance and Displacement?

Distance is a scalar quantity as it is independent of the direction where as Displacement is a vector quantity as it has both magnitude and direction.

4. How is the Displacement Vector different from the Position Vector?

The displacement vector determines the direction of change in position of a vector, on the other hand position vector determines the position of a vector in space with reference to a specific position.

5. What is the Difference between Collinear and Coplanar Vectors?

Collinear vectors are the vectors which lie on the same line or are parallel to the same line where as coplanar vectors are a set of vectors that lie on the same plane irrespective of their direction.