Turing Machine to check whether given string is Even Palindrome or not
Last Updated :
10 May, 2020
A string w is called
palindrome if reading w from left to right gives the same result as reading w from right to left.An even palindrome has even number of symbols.
Examples:
Input : abaaba
Output :YES
Input :abba
Output :YES
Input :abbaba
Output :NO
Input :Empty String or 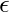 Output :YES
Output :YES
Basic Representation :
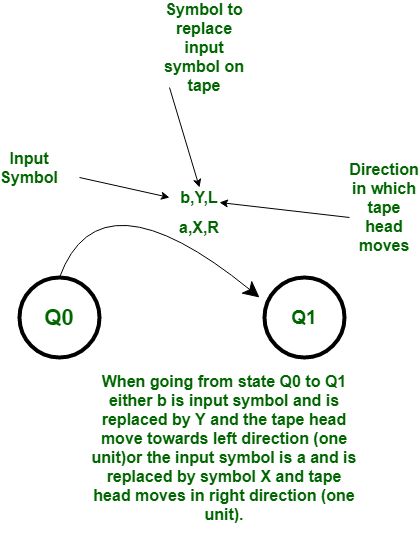 Start of Computation :
Start of Computation :
The tape contains the input string w, the tape head is on the leftmost symbol of w, and the Turing machine is in the start state Q0.
Basic Idea :
The tape head reads the leftmost symbol of w, deletes this symbol and “remembers” it by means of a state. Then the tape head moves to rightmost symbol and tests whether it is equal to the (already deleted) leftmost symbol.
If they are equal, then the rightmost symbol is deleted, the tape head moves to the new leftmost symbol, and the whole process is repeated . Else the machine can’t reach the final state and the string will be rejected.
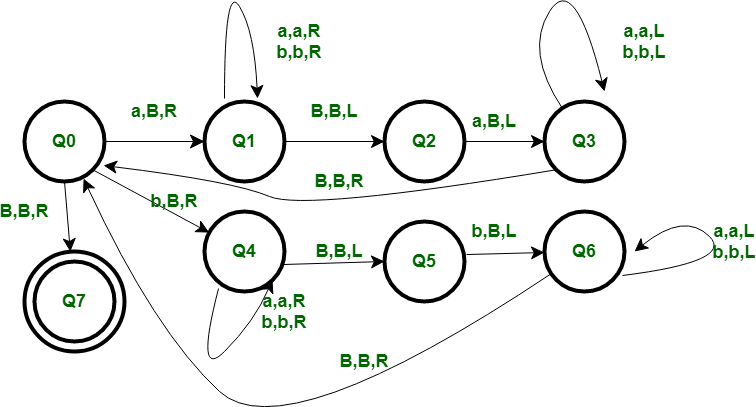 Meanings of symbols used:
Meanings of symbols used:
R, L – direction of movement of one unit on either side .
B-Blank
a, b-symbols whose combination string is to be tested
Working Procedure :
- Step-1:
We start with Q0 state if we get a symbol “a” as input then there should also be “a” at the ending of the string then only the string is palindrome and we have to verify that. We first make the current input “a” to B blank and go to state Q1 move rightwards to traverse the string till we reach the end. Keep the input symbols a or b whichever comes in ways should be remain unchanged.
We can reach the end of the string when we get Blank as the input symbol then we change state to Q2 and test if the previous symbol is “a” then we change to state Q3 and then only we will replace it by Blank and we have successfully tested that string is palindrome till this point now we will traverse back or leftwards (keeping a and b unchanged which comes in way) on the string and till we get Blank which is the symbol which we made Blank at the start and we change state to Q0.Now we repeat the same procedure for “b” as input.
- Step-2:
Till this point if the string was palindrome then it would have returned to state Q0 after all iterations and if the string was not palindrome then we would stuck at the states Q2 or Q5 and when stuck at these points we cant reach Q0 and hence can not reach the final state or acceptance state Q7.
- Step-3:
If the string was palindrome then there will be only Blank symbol left and hence we test it at Q0 if we get blank hence the string gets accepted and is palindrome, at this point there is one more condition is included which is of null string or
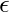 as empty string is also palindrome hence gets accepted.
as empty string is also palindrome hence gets accepted.
Share your thoughts in the comments
Please Login to comment...