Construct a Turing Machine for language L = {ww | w ∈ {0,1}}
Last Updated :
29 Oct, 2021
Prerequisite – Turing Machine
The language L = {ww | w ∈ {0, 1}} tells that every string of 0’s and 1’s which is followed by itself falls under this language. The logic for solving this problem can be divided into 2 parts:
- Finding the mid point of the string
- After we have found the mid point we match the symbols
Example – Lets understand it with the help of an example. Lets string 1 0 1 1 0 1, so w = 1 0 1 and string is of form (ww).
The first thing that we do is to find the midpoint. For this, we convert 1 in the beginning into Y and move right till the end of the string. Here we convert 1 into y.
Now our string would look like Y 0 1 1 0 Y. Now move left till, find a X or Y. When we do so, convert the 0 or 1 right of it to X or Y respectively and then do the same on the right end. Now our string would look like Y X 1 1 X Y. Thereafter, convert these 1’s also and finally it would look like Y X Y Y X Y.
At this point, you have achieved the first objective which was to find the midpoint. Now convert all X and Y on the left of midpoint into 0 and 1 respectively, so string becomes 1 0 1 Y X Y. Now, convert the 1 into Y and move right till, find Y in the beginning of the right part of the string and convert this Y into a blank (denoted by B). Now string looks like Y 0 1 B X Y.
Similarly, apply this on 0 and x followed by 1 and Y. After this string looks like Y X Y B B B. Now that you have no 0 and 1 and all X and Y on the right part of the string are converted into blanks so our string will be accepted.
Assumption: We will replace 0 by X and 1 by Y.
Approach Used –
The first thing is to find the midpoint of the string, convert a 0 or 1 from the beginning of the string into X or Y respectively and a corresponding 0 or 1 into X or Y from the end of the string. After continuously doing it a point is reached when all 0’s and 1’s have been converted into X and Y respectively. At this point, you are on the midpoint of the string. So, our first objective is fulfilled.
Now, convert all X’s and Y’s on the left of the midpoint into 0’s and 1’s. At this point the first half the string is in the form of 0 and 1. The second half of the string is in the form of X and Y.
Now, start from the beginning of the string. If you have a 0 then convert it into X and move right till reaching the second half, here if we find X then convert it into a blank(B). Then traverse back till find an X or a Y. We convert the 0 or 1 on the right of it into X or Y respectively and correspondingly, convert its X or Y in the second half of string into a blank(B).
Keep doing this till converted all symbols on the left part of the string into X and Y and all symbols on the right of string into blanks. If any one part is completely converted but still some symbols in the other half are left unchanged then the string will not be accepted. If you did not find an X or Y in the second half for a corresponding 0 or 1 respectively in the first half. Then also string will not be accepted.
Examples:
Input : 1 1 0 0 1 1 0 0
Output : Accepted
Input : 1 0 1 1 1 0 1
Output : Not accepted
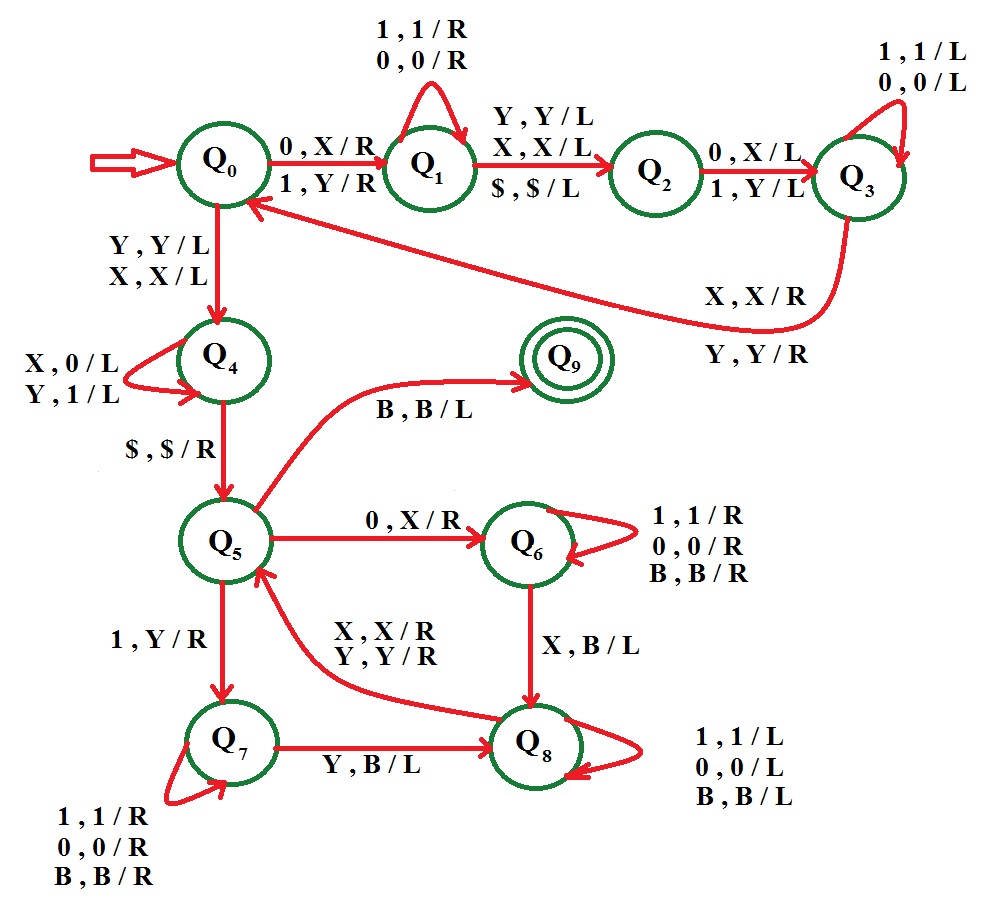
- Step-1:
If the symbol is 0 replace it by X and move right
If the symbol is 1 replace it by Y and move right,
Go to state Q1 and step 2
———————————————
If the symbol is X replace it by X and move left or
If the symbol is Y replace it by Y and move left,
Go to state Q4 and step 5
- Step-2:
If the symbol is 0 replace it by 0 and move right, remain on the same state
If the symbol is 1 replace it by 1 and move right, remain on the same state
———————————————
If the symbol is X replace it by X and move left or
If the symbol is Y replace it by Y and move left or
If the symbol is $ replace it by $ and move left, Go to state Q2 and step 3
- Step-3:
If symbol is 0 replace it by X and move left, or
If symbol is 1 replace it by Y and move left,
Go to state Q3 and step 4
- Step-4:
If the symbol is 0 replace it by 0 and move left, remain on the same state
If the symbol is 1 replace it by 1 and move left, remain on the same state
———————————————
If the symbol is X replace it by X and move right or
If the symbol is Y replace it by Y and move right,
Go to state Q0 and step 1
- Step-5:
If symbol is X replace it by X and move left or
If symbol is Y replace it by Y and move left
Go to state Q4 and step 6
- Step-6:
If symbol is X replace it by 0 and move left, remain on same state
If symbol is Y replace it by 1 and move left, remain on same state
– – – – – – – – – — – – – – – – – – – —
If symbol is $ replace it by $ and move right
Go to state Q4 and step 7
- Step-7:
If symbol is 0 replace it by X and move right, go to state Q6 and step 8
If symbol is 1 replace it by Y and move right, go to state Q7 and step 9
– – – – – – – – – — – – – – – – – – – —
If symbol is B replace it by B and move left, STRING ACCEPTED, GO TO FINAL STATE Q9
- Step-8:
If symbol is 0 replace it by 0 and move right, remain on same state
If symbol is 1 replace it by 1 and move right, remain on same state
If symbol is B replace it by B and move right, remain on same state
– — – – – – – – – – – – – – – – – – – –
If symbol is X replace it by B and move left
Go to state Q8 and step 10
- Step-9:
If symbol is 0 replace it by 0 and move right, remain on same state
If symbol is 1 replace it by 1 and move right, remain on same state
If symbol is B replace it by B and move right, remain on same state
– — – – – – – – – – – – – – – – – – – –
If symbol is Y replace it by B and move left
Go to state Q8 and step 10
- Step-10:
If symbol is 0 replace it by 0 and move left, remain on same state
If symbol is 1 replace it by 1 and move left, remain on same state
If symbol is B replace it by B and move left, remain on same state
– — – – – – – – – – – – – – – – – – – –
If symbol is Y replace it by Y and move right or
If symbol is X replace it by X and move right
Go to state Q5 and step 7
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...