Tournament Tree (Winner Tree) and Binary Heap
Last Updated :
02 Jun, 2023
Given a team of N players. How many minimum games are required to find the second-best player?
We can use adversary arguments based on the tournament tree (Binary Heap). A Tournament tree is a form of min (max) heap which is a complete binary tree. Every external node represents a player and the internal node represents the winner.
In a tournament tree, every internal node contains the winner and every leaf node contains one player. There will be N – 1 internal node in a binary tree with N leaf (external) nodes.
For details see this post (put n = 2 in the equation given in the post). It is obvious that to select the best player among N players, (N – 1) players are to be eliminated, i.e. we need a minimum of (N – 1) games (comparisons). Mathematically we can prove it. In a binary tree, I = E – 1, where I is a number of internal nodes and E is a number of external nodes. It means to find the maximum or minimum element of an array, we need N – 1 (internal nodes) comparisons.
Second Best Player The information explored during best player selection can be used to minimize the number of comparisons in tracing the next best players. For example, we can pick the second-best player in (N + log2N – 2) comparisons. The following diagram displays a tournament tree (winner tree) as a max heap. Note that the concept of the loser tree is different.

The above tree contains 4 leaf nodes that represent players and have 3 levels 0, 1, and 2. Initially, 2 games are conducted at level 2, one between 5 and 3 and another one between 7 and 8. In the next move, one more game is conducted between 5 and 8 to conclude the final winner. Overall we need 3 comparisons.
For the second-best player we need to trace the candidates who participated with the final winner, which leads to 7 as the second-best.
Median of Sorted Arrays Tournament tree can effectively be used to find the median of sorted arrays. Assume, given M sorted arrays of equal size L (for simplicity). We can attach all these sorted arrays to the tournament tree, one array per leaf. We need a tree of height CEIL (log2M) to have at least M external nodes. Consider an example. Given 3 (M = 3) sorted integer arrays of maximum size 5 elements.
{ 2, 5, 7, 11, 15 } ---- Array1
{1, 3, 4} ---- Array2
{6, 8, 12, 13, 14} ---- Array3
What should be the height of the tournament tree? We need to construct a tournament tree of height log23 .= 1.585 = 2 rounded to the next integer. A binary tree of height 2 will have 4 leaves to which we can attach the arrays as shown in the below figure.
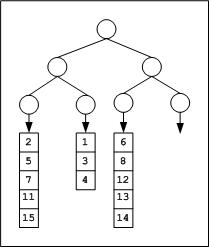
After the first tournament, the tree appears as below,

We can observe that the winner is from Array2. Hence the next element from Array2 will dive in and games will be played along the winner path of the previous tournament.
Note that infinity is used as a sentinel element. Based on data being held in nodes, we can select the sentinel character. For example, we usually store the pointers in nodes rather than keys, so NULL can serve as a sentinel. If any of the array exhausts we will fill the corresponding leaf and upcoming internal nodes with sentinel. After the second tournament, the tree appears as below,

The next winner is from Array1, so the next element of the Array1 array which is 5 will dive into the next round, and the next tournament played along the path of 2. The tournaments can be continued till we get the median element which is (5+3+5)/2 = 7th element.
Note that there are even better algorithms for finding the median of the union of sorted arrays, for details see the related links given below.
In general with M sorted lists of size L1, L2 … Lm requires time complexity of O((L1 + L2 + … + Lm) * logM) to merge all the arrays and O(m*logM) time to find median, where m is median position.
elect the smallest one million elements from one billion unsorted elements: As a simple solution, we can sort a billion numbers and select the first one million. On a limited memory system sorting a billion elements and picking the first one million seems to be impractical. We can use the tournament tree approach. At any time only elements of a tree are in memory.
Split the large array (perhaps stored on disk) into smaller size arrays of size one million each (or even smaller that can be sorted by the machine). Sort these 1000 small size arrays and store them on disk as individual files. Construct a tournament tree that can have at least 1000 leaf nodes (tree to be of height 10 since 29 < 1000 < 210, if the individual file size is even smaller we will need more leaf nodes). Every leaf node will have an engine that picks the next element from the sorted file stored on disk.
We can play the tournament tree game to extract the first one million elements. Total cost = sorting 1000 lists of one million each + tree construction + tournaments.
Application of Tournament Trees:
- Used for sorting purposes.
- Used to find the largest and smallest element
- It may also be used in m-way merges
- Applied in the Truck Loading problem
Implementation:
We need to build the tree in a bottom-up manner. All the leaf nodes were filled first. Start at the left extreme of the tree and fill along the breadth (i.e. from 2k-1 to 2k – 1 where k is the depth of the tree) and play the game. After practicing with a few examples it will be easy to write code. Implementation is discussed in the below code Second minimum element using minimum comparisons
Related Posts : Find the smallest and second smallest element in an array. Second minimum element using minimum comparisons — by Venki.
Share your thoughts in the comments
Please Login to comment...