Time Complexity of building a heap
Last Updated :
17 Jun, 2022
Consider the following algorithm for building a Heap of an input array A.
BUILD-HEAP(A)
heapsize := size(A);
for i := floor(heapsize/2) downto 1
do HEAPIFY(A, i);
end for
END
A quick look over the above algorithm suggests that the running time is 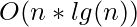 since each call to Heapify costs
since each call to Heapify costs 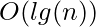 and Build-Heap makes
and Build-Heap makes 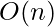 such calls.
such calls.
This upper bound, though correct, is not asymptotically tight.
We can derive a tighter bound by observing that the running time of Heapify depends on the height of the tree ‘h’ (which is equal to lg(n), where n is a number of nodes) and the heights of most sub-trees are small. The height ’h’ increases as we move upwards along the tree. Line-3 of Build-Heap runs a loop from the index of the last internal node (heapsize/2) with height=1, to the index of root(1) with height = lg(n). Hence, Heapify takes a different time for each node, which is:
For finding the Time Complexity of building a heap, we must know the number of nodes having height h. For this we use the fact that, A heap of size n has at most 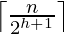 nodes with height h.
nodes with height h.
a to derive the time complexity, we express the total cost of Build-Heap as-
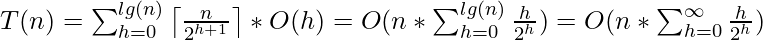
Step 2 uses the properties of the Big-Oh notation to ignore the ceiling function and the constant 2(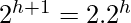 ). Similarly in Step three, the upper limit of the summation can be increased to infinity since we are using Big-Oh notation. Sum of infinite G.P. (x < 1)
). Similarly in Step three, the upper limit of the summation can be increased to infinity since we are using Big-Oh notation. Sum of infinite G.P. (x < 1)
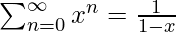
On differentiating both sides and multiplying by x, we get
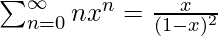
Putting the result obtained in (3) back in our derivation (1), we get
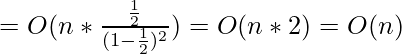
Hence Proved that the Time complexity for Building a Binary Heap is 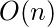 .
.
Share your thoughts in the comments
Please Login to comment...