Sum of all Primes in a given range using Sieve of Eratosthenes

Given a range [L, R]. The task is to find the sum of all the prime numbers in the given range from L to R both inclusive.
Examples: 

Input : L = 10, R = 20
Output : Sum = 60
Prime numbers between [10, 20] are:
11, 13, 17, 19
Therefore, sum = 11 + 13 + 17 + 19 = 60

Input : L = 15, R = 25
Output : Sum = 59

A Simple Solution is to traverse from L to R, check if the current number is prime. If yes, add it to 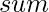. Finally, print the sum.
An Efficient Solution is to use Sieve of Eratosthenes to find all primes up to a given limit. Then, compute a prefix sum array to store sum till every value before the limit. Once we have prefix array, We just need to return prefix[R] – prefix[L-1].
Note: prefix[i] will store the sum of all prime numbers from 1 to .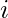
Below is the implementation of the above approach: 

C++

// CPP program to find sum of primes
// in range L to R
#include <bits/stdc++.h>
using namespace std;

const int MAX = 10000;

// prefix[i] is going to store sum of primes
// till i (including i).
int prefix[MAX + 1];

// Function to build the prefix sum array
void buildPrefix()
{
    // Create a boolean array "prime[0..n]". A
    // value in prime[i] will finally be false
    // if i is Not a prime, else true.
    bool prime[MAX + 1];
    memset(prime, true, sizeof(prime));

    for (int p = 2; p * p <= MAX; p++) {

        // If prime[p] is not changed, then
        // it is a prime
        if (prime[p] == true) {

            // Update all multiples of p
            for (int i = p * 2; i <= MAX; i += p)
                prime[i] = false;
        }
    }

    // Build prefix array
    prefix[0] = prefix[1] = 0;
    for (int p = 2; p <= MAX; p++) {
        prefix[p] = prefix[p - 1];
        if (prime[p])
            prefix[p] += p;
    }
}

// Function to return sum of prime in range
int sumPrimeRange(int L, int R)
{
    buildPrefix();

    return prefix[R] - prefix[L - 1];
}

// Driver code
int main()
{
    int L = 10, R = 20;

    cout << sumPrimeRange(L, R) << endl;

    return 0;
}

Java

// Java program to find sum of primes
// in range L to R

import java.util.*;
import java.lang.*;
import java.io.*;

class GFG{

static final int MAX = 10000;

// prefix[i] is going to store sum of primes
// till i (including i).
static int prefix[]=new int[MAX + 1];

// Function to build the prefix sum array
static void buildPrefix()
{
    // Create a boolean array "prime[0..n]". A
    // value in prime[i] will finally be false
    // if i is Not a prime, else true.
    boolean prime[] = new boolean[MAX + 1];

    for(int i = 0; i < MAX+1; i++)
    prime[i] = true;

    for (int p = 2; p * p <= MAX; p++) {

        // If prime[p] is not changed, then
        // it is a prime
        if (prime[p] == true) {

            // Update all multiples of p
            for (int i = p * 2; i <= MAX; i += p)
                prime[i] = false;
        }
    }

    // Build prefix array
    prefix[0] = prefix[1] = 0;
    for (int p = 2; p <= MAX; p++) {
        prefix[p] = prefix[p - 1];
        if (prime[p] == true)
            prefix[p] += p;
    }
}

// Function to return sum of prime in range
static int sumPrimeRange(int L, int R)
{
    buildPrefix();

    return prefix[R] - prefix[L - 1];
}

// Driver code
public static void main(String args[])
{
    int L = 10, R = 20;

    System.out.println (sumPrimeRange(L, R));

}
}

Python3

# Python 3 program to find sum of primes
# in range L to R
from math import sqrt

MAX = 10000

# prefix[i] is going to store sum of primes
# till i (including i).
prefix = [0 for i in range(MAX + 1)]

# Function to build the prefix sum array
def buildPrefix():

    # Create a boolean array "prime[0..n]". A
    # value in prime[i] will finally be false
    # if i is Not a prime, else true.
    prime = [True for i in range(MAX + 1)]

    for p in range(2,int(sqrt(MAX)) + 1, 1):

        # If prime[p] is not changed, then
        # it is a prime
        if (prime[p] == True):

            # Update all multiples of p
            for i in range(p * 2, MAX + 1, p):
                prime[i] = False

    # Build prefix array
    prefix[0] = 0
    prefix[1] = 0
    for p in range(2, MAX + 1, 1):
        prefix[p] = prefix[p - 1]
        if (prime[p]):
            prefix[p] += p

# Function to return sum of prime in range
def sumPrimeRange(L, R):
    buildPrefix()

    return prefix[R] - prefix[L - 1]

# Driver code
if __name__ == '__main__':
    L = 10
    R = 20
    print(sumPrimeRange(L, R))

# This code is contributed by
# Surendra_Gangwar

C#

// C# program to find sum of
// primes in range L to R
using System;
class GFG
{

static int MAX = 10000;

// prefix[i] is going to
// store sum of primes
// till i (including i).
static int []prefix = new int[MAX + 1];

// Function to build the
// prefix sum array
static void buildPrefix()
{
    // Create a boolean array "prime[0..n]".
    // A value in prime[i] will finally
    // be false if i is Not a prime,
    // else true.
    bool []prime = new bool[MAX + 1];

    for(int i = 0; i < MAX+1; i++)
    prime[i] = true;

    for (int p = 2; p * p <= MAX; p++)
    {

        // If prime[p] is not changed,
        // then it is a prime
        if (prime[p] == true)
        {

            // Update all multiples of p
            for (int i = p * 2; i <= MAX; i += p)
                prime[i] = false;
        }
    }

    // Build prefix array
    prefix[0] = prefix[1] = 0;
    for (int p = 2; p <= MAX; p++)
    {
        prefix[p] = prefix[p - 1];
        if (prime[p] == true)
            prefix[p] += p;
    }
}

// Function to return sum
// of prime in range
static int sumPrimeRange(int L, int R)
{
    buildPrefix();

    return prefix[R] - prefix[L - 1];
}

// Driver code
public static void Main()
{
    int L = 10, R = 20;

    Console.WriteLine(sumPrimeRange(L, R));
}
}

// This code is contributed
// by anuj_67

Javascript

<script>
// Jacascript program to find sum of primes

MAX = 10000;

// prefix[i] is going to store sum of primes
// till i (including i).
prefix = new Array(MAX + 1);

// Function to build the prefix sum array
function buildPrefix()
{
    // Create a boolean array "prime[0..n]". A
    // value in prime[i] will finally be false
    // if i is Not a prime, else true.
    prime = new Array(MAX + 1);
    prime.fill(true);

    for (var p = 2; p * p <= MAX; p++) {

        // If prime[p] is not changed, then
        // it is a prime
        if (prime[p] == true) {

            // Update all multiples of p
            for (var i = p * 2; i <= MAX; i += p)
                prime[i] = false;
        }
    }

    // Build prefix array
    prefix[0] = prefix[1] = 0;
    for (var p = 2; p <= MAX; p++) {
        prefix[p] = prefix[p - 1];
        if (prime[p])
            prefix[p] += p;
    }
}

// Function to return sum of prime in range
function sumPrimeRange(L, R)
{
    buildPrefix();
    return prefix[R] - prefix[L - 1];
}

var L = 10, R = 20;
document.write( sumPrimeRange(L, R) + "<br>");

// This code is contributed by SoumikMondal
</script>

Output:

60

Time and Space complexity will be as same as in Sieve Of Eratosthenes

Time Complexity : n*log(log(n)) (where n = MAX, because we are building sieve to that limit)

Auxiliary Space : O(n)