Smallest Derangement of Sequence
Last Updated :
21 Dec, 2022
Given the sequence
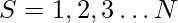
find the lexicographically smallest (earliest in dictionary order) derangement of
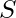
A derangement of S is any permutation of S such that no two elements in S and its permutation occur at the same position.
Examples:
Input: 3
Output : 2 3 1
Explanation: The Sequence is 1 2 3.
Possible permutations are (1, 2, 3), (1, 3, 2),
(2, 1, 3), (2, 3, 1), (3, 1, 2) (3, 2, 1).
Derangements are (2, 3, 1), (3, 1, 2).
Smallest Derangement: (2, 3, 1)
Input : 5
Output : 2 1 4 5 3.
Explanation: Out of all the permutations of
(1, 2, 3, 4, 5), (2, 1, 4, 5, 3) is the first derangement.
Method 1:
We can modify the method shown in this article: Largest Derangement
Using a min heap we can successively get the least element and place them in more significant positions, taking care that the property of derangement is maintained.
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
void generate_derangement(int N)
{
int S[N + 1];
priority_queue<int, vector<int>, greater<int> > PQ;
for (int i = 1; i <= N; i++) {
S[i] = i;
PQ.push(S[i]);
}
int D[N + 1];
for (int i = 1; i <= N; i++) {
int d = PQ.top();
PQ.pop();
if (d != S[i] || i == N) {
D[i] = d;
}
else {
D[i] = PQ.top();
PQ.pop();
PQ.push(d);
}
}
if (D[N] == S[N])
swap(D[N-1], D[N]);
for (int i = 1; i <= N; i++)
printf("%d ", D[i]);
printf("\n");
}
int main()
{
generate_derangement(10);
return 0;
}
|
Java
import java.util.*;
class GFG{
static void generate_derangement(int N)
{
int []S = new int[N + 1];
PriorityQueue<Integer> PQ =
new PriorityQueue <>();
for (int i = 1; i <= N; i++)
{
S[i] = i;
PQ.add(S[i]);
}
int []D = new int[N + 1];
for (int i = 1; i <= N; i++)
{
int d = PQ.peek();
PQ.remove();
if (d != S[i] || i == N)
{
D[i] = d;
}
else
{
D[i] = PQ.peek();
PQ.remove();
PQ.add(d);
}
}
if (D[N] == S[N])
{
int t = D[N - 1];
D[N - 1] = D[N];
D[N] = t;
}
for (int i = 1; i <= N; i++)
System.out.printf("%d ", D[i]);
System.out.printf("\n");
}
public static void main(String[] args)
{
generate_derangement(10);
}
}
|
Python3
def generate_derangement(N) :
S = [i for i in range(N + 1)]
PQ = []
for i in range(1, N + 1) :
PQ.append(S[i])
D = [0] * (N + 1)
PQ.sort()
for i in range(1, N + 1) :
PQ.sort()
d = PQ[0]
del PQ[0]
if (d != S[i]) or (i == N) :
D[i] = d
else :
PQ.sort()
D[i] = PQ[0]
del PQ[0]
PQ.append(d)
if D[N] == S[N] :
t = D[N - 1]
D[N - 1] = D[N]
D[N] = t
for i in range(1, N + 1) :
print(D[i], end = " ")
print()
generate_derangement(10)
|
C#
using System;
using System.Collections.Generic;
class GFG{
static void generate_derangement(int N)
{
int []S = new int[N + 1];
List<int> PQ = new List <int>();
for(int i = 1; i <= N; i++)
{
S[i] = i;
PQ.Add(S[i]);
}
int []D = new int[N + 1];
PQ.Sort();
for(int i = 1; i <= N; i++)
{
PQ.Sort();
int d = PQ[0];
PQ.RemoveAt(0);
if (d != S[i] || i == N)
{
D[i] = d;
}
else
{
PQ.Sort();
D[i] = PQ[0];
PQ.RemoveAt(0);
PQ.Add(d);
}
}
if (D[N] == S[N])
{
int t = D[N - 1];
D[N - 1] = D[N];
D[N] = t;
}
for(int i = 1; i <= N; i++)
Console.Write(D[i] + " ");
Console.Write("\n");
}
public static void Main(String[] args)
{
generate_derangement(10);
}
}
|
Javascript
<script>
function generate_derangement(N)
{
let S = new Array(N + 1);
let PQ =[];
for (let i = 1; i <= N; i++)
{
S[i] = i;
PQ.push(S[i]);
}
PQ.sort(function(a,b){return a-b;});
let D = new Array(N + 1);
for (let i = 1; i <= N; i++)
{
let d = PQ.shift();
if (d != S[i] || i == N)
{
D[i] = d;
}
else
{
D[i] = PQ.shift();
PQ.push(d);
}
PQ.sort(function(a,b){return a-b;});
}
if (D[N] == S[N])
{
let t = D[N - 1];
D[N - 1] = D[N];
D[N] = t;
}
for (let i = 1; i <= N; i++)
document.write( D[i]+" ");
document.write("<br>");
}
generate_derangement(10);
</script>
|
Output2 1 4 3 6 5 8 7 10 9
Time Complexity: O(N * log N).
Auxiliary Space: O(N)
Method 2:
Since we are given a very specific sequence i.e
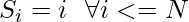
We can calculate the answer even more efficiently.
Divide the original sequence into pairs of two elements, and then swap the elements of each pair.
If N is odd then the last pair needs to be swapped again.
Pictorial Representation


Complexity: We perform at most N/2 + 1 swaps, so the complexity is O(N).
Why does this method work
This method is a very specific application of method 1 and is based on observation. Given the nature of the sequence, at position i we already know the least element that can be put, which is either i+1 or i-1. Since we are already given the least permutation of S it is clear that the derangement must start from 2 and not 1 ie of the form i+1 (i = 1). The next element will be of form i – 1 . The element after this will be i + 1 and then next i – 1. This pattern will continue until the end.
This operation is most easily understood as the swapping of adjacent elements of pairs of elements of S.
If we can determine the least element in constant time, then the complexity overhead from the heap is eliminated. Hence, from O(N * log N) the complexity reduces to O(N).
Below is the implementation of the above approach:
Implementation:
C++
#include <bits/stdc++.h>
void generate_derangement(int N)
{
int S[N + 1];
for (int i = 1; i <= N; i++)
S[i] = i;
int D[N + 1];
for (int i = 1; i <= N; i += 2) {
if (i == N && i%N!=0) {
int temp=D[N];
D[N] = D[N - 1];
D[N - 1] = temp;
}
else {
D[i] = i + 1;
D[i + 1] = i;
}
}
for (int i = 1; i <= N; i++)
printf("%d ", D[i]);
printf("\n");
}
int main()
{
generate_derangement(10);
return 0;
}
|
Java
class GFG
{
static void generate_derangement(int N)
{
int S[] = new int[N + 1];
for (int i = 1; i <= N; i++)
S[i] = i;
int D[] = new int[N + 1];
for (int i = 1; i <= N; i += 2)
{
if (i == N)
{
D[N] = S[N - 1];
D[N - 1] = S[N];
}
else
{
D[i] = i + 1;
D[i + 1] = i;
}
}
for (int i = 1; i <= N; i++)
System.out.print(D[i] + " ");
System.out.println();
}
public static void main(String[] args)
{
generate_derangement(10);
}
}
|
Python3
def generate_derangement(N):
S = [0] * (N + 1)
for i in range(1, N + 1):
S[i] = i
D = [0] * (N + 1)
for i in range(1, N + 1, 2):
if i == N:
D[N] = S[N - 1]
D[N - 1] = S[N]
else:
D[i] = i + 1
D[i + 1] = i
for i in range(1, N + 1):
print(D[i], end = " ")
print()
if __name__ == '__main__':
generate_derangement(10)
|
C#
using System;
class GFG
{
static void generate_derangement(int N)
{
int[] S = new int[N + 1];
for (int i = 1; i <= N; i++)
S[i] = i;
int[] D = new int[N + 1];
for (int i = 1; i <= N; i += 2)
{
if (i == N)
{
D[N] = S[N - 1];
D[N - 1] = S[N];
}
else
{
D[i] = i + 1;
D[i + 1] = i;
}
}
for (int i = 1; i <= N; i++)
Console.Write(D[i] + " ");
Console.WriteLine();
}
public static void Main()
{
generate_derangement(10);
}
}
|
PHP
<?php
function generate_derangement($N)
{
$S = array();
for ($i = 1; $i <= $N; $i++)
$S[$i] = $i;
$D = array();
for ($i = 1; $i <= $N; $i += 2)
{
if ($i == $N)
{
$D[$N] = $S[$N - 1];
$D[$N - 1] = $S[$N];
}
else
{
$D[$i] = $i + 1;
$D[$i + 1] = $i;
}
}
for ($i = 1; $i <= $N; $i++)
echo $D[$i] . " ";
echo "\n";
}
generate_derangement(10);
?>
|
Javascript
<script>
function generate_derangement(N)
{
let S = [];
for (let i = 1; i <= N; i++)
S[i] = i;
let D = [];
for (let i = 1; i <= N; i += 2)
{
if (i == N)
{
D[N] = S[N - 1];
D[N - 1] = S[N];
}
else
{
D[i] = i + 1;
D[i + 1] = i;
}
}
for (let i = 1; i <= N; i++)
document.write(D[i] + " ");
document.write("<br/>");
}
generate_derangement(10);
</script>
|
Output2 1 4 3 6 5 8 7 10 9
Time Complexity: O(N)
Auxiliary Space: O(N)
Note: The auxiliary space can be reduced to O(1) if we perform the swapping operations on S itself.
Share your thoughts in the comments
Please Login to comment...