Largest Derangement of a Sequence
Last Updated :
22 Dec, 2022
Given any sequence, find the largest derangement of .
A derangement 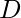 is any permutation of, such that no two elements at the same position in
is any permutation of, such that no two elements at the same position in 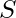 and
and 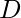 are equal.
are equal.
The Largest Derangement is such that.
Examples:
Input : seq[] = {5, 4, 3, 2, 1}
Output : 4 5 2 1 3
Input : seq[] = {56, 21, 42, 67, 23, 74}
Output : 74, 67, 56, 42, 21, 23
Since we are interested in generating the largest derangement, we start putting larger elements in more significant positions.
Start from left, at any position 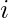 place the next largest element among the values of the sequence which have not yet been placed in positions before.
place the next largest element among the values of the sequence which have not yet been placed in positions before.
To scan all positions takes N iteration. In each iteration we are required to find a maximum number, so a trivial implementation would be 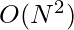 complexity,
complexity,
However, if we use a data structure like max-heap to find the maximum element, then the complexity reduces to 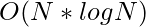
Below is the implementation.
C++
#include <bits/stdc++.h>
using namespace std;
void printLargest(int seq[], int N)
{
int res[N];
std::priority_queue<int> pq;
for (int i = 0; i < N; i++)
pq.push(seq[i]);
for (int i = 0; i < N; i++) {
int d = pq.top();
pq.pop();
if (d != seq[i] || i == N - 1) {
res[i] = d;
} else {
res[i] = pq.top();
pq.pop();
pq.push(d);
}
}
if (res[N - 1] == seq[N - 1]) {
res[N - 1] = res[N - 2];
res[N - 2] = seq[N - 1];
}
printf("\nLargest Derangement \n");
for (int i = 0; i < N; i++)
printf("%d ", res[i]);
}
int main()
{
int seq[] = { 92, 3, 52, 13, 2, 31, 1 };
int n = sizeof(seq)/sizeof(seq[0]);
printLargest(seq, n);
return 0;
}
|
Java
import java.io.*;
import java.util.Collections;
import java.util.PriorityQueue;
class GFG{
public static void printLargest(int a[],int n)
{
PriorityQueue<Integer> pq = new PriorityQueue<>(
Collections.reverseOrder());
for(int i = 0; i < n; i++)
{
pq.add(a[i]);
}
int res[] = new int[n];
for(int i = 0; i < n; i++)
{
int p = pq.peek();
pq.remove();
if (p != a[i] || i == n - 1)
{
res[i] = p;
}
else
{
res[i] = pq.peek();
pq.remove();
pq.add(p);
}
}
if (res[n - 1] == a[n - 1])
{
res[n - 1] = res[n - 2];
res[n - 2] = a[n - 1];
}
System.out.println("Largest Derangement");
for(int i = 0; i < n; i++)
{
System.out.print(res[i] + " ");
}
}
public static void main(String[] args)
{
int n = 7;
int seq[] = { 92, 3, 52, 13, 2, 31, 1 };
printLargest(seq, n);
}
}
|
Python3
def printLargest(seq, N) :
res = [0]*N
pq = []
for i in range(N) :
pq.append(seq[i])
for i in range(N) :
pq.sort()
pq.reverse()
d = pq[0]
del pq[0]
if (d != seq[i] or i == N - 1) :
res[i] = d
else :
res[i] = pq[0]
del pq[0]
pq.append(d)
if (res[N - 1] == seq[N - 1]) :
res[N - 1] = res[N - 2]
res[N - 2] = seq[N - 1]
print("Largest Derangement")
for i in range(N) :
print(res[i], end = " ")
seq = [ 92, 3, 52, 13, 2, 31, 1 ]
n = len(seq)
printLargest(seq, n)
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static void printLargest(int[] seq, int N)
{
int[] res = new int[N];
List<int> pq = new List<int>();
for (int i = 0; i < N; i++)
pq.Add(seq[i]);
for (int i = 0; i < N; i++)
{
pq.Sort();
pq.Reverse();
int d = pq[0];
pq.RemoveAt(0);
if (d != seq[i] || i == N - 1)
{
res[i] = d;
}
else
{
res[i] = pq[0];
pq.RemoveAt(0);
pq.Add(d);
}
}
if (res[N - 1] == seq[N - 1])
{
res[N - 1] = res[N - 2];
res[N - 2] = seq[N - 1];
}
Console.WriteLine("Largest Derangement");
for (int i = 0; i < N; i++)
Console.Write(res[i] + " ");
}
static void Main()
{
int[] seq = { 92, 3, 52, 13, 2, 31, 1 };
int n = seq.Length;
printLargest(seq, n);
}
}
|
Javascript
<script>
function printLargest(seq, N) {
let res = new Array(N);
let pq = new Array();
for (let i = 0; i < N; i++)
pq.push(seq[i]);
for (let i = 0; i < N; i++) {
pq.sort((a, b) => a - b);
pq.reverse();
let d = pq[0];
pq.shift();
if (d != seq[i] || i == N - 1) {
res[i] = d;
}
else {
res[i] = pq[0];
pq.shift();
pq.push(d);
}
}
if (res[N - 1] == seq[N - 1]) {
res[N - 1] = res[N - 2];
res[N - 2] = seq[N - 1];
}
document.write("Largest Derangement<br>");
for (let i = 0; i < N; i++)
document.write(res[i] + " ");
}
let seq = [92, 3, 52, 13, 2, 31, 1];
let n = seq.length;
printLargest(seq, n);
</script>
|
OutputLargest Derangement
52 92 31 3 13 1 2
Time Complexity: O(n log n)
Auxiliary Space: O(N), because, we use an N size array to store results.
Note:
The method can be easily modified to obtain the smallest derangement as well.
Instead of a Max Heap, we should use a Min Heap to consecutively get minimum elements
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...