Prerequisite – Parsing | Set 2 (Bottom Up or Shift Reduce Parsers)
Shift Reduce parser attempts for the construction of parse in a similar manner as done in bottom-up parsing i.e. the parse tree is constructed from leaves(bottom) to the root(up). A more general form of the shift-reduce parser is the LR parser.
This parser requires some data structures i.e.
- An input buffer for storing the input string.
- A stack for storing and accessing the production rules.
Basic Operations –
- Shift: This involves moving symbols from the input buffer onto the stack.
- Reduce: If the handle appears on top of the stack then, its reduction by using appropriate production rule is done i.e. RHS of a production rule is popped out of a stack and LHS of a production rule is pushed onto the stack.
- Accept: If only the start symbol is present in the stack and the input buffer is empty then, the parsing action is called accept. When accepted action is obtained, it is means successful parsing is done.
- Error: This is the situation in which the parser can neither perform shift action nor reduce action and not even accept action.
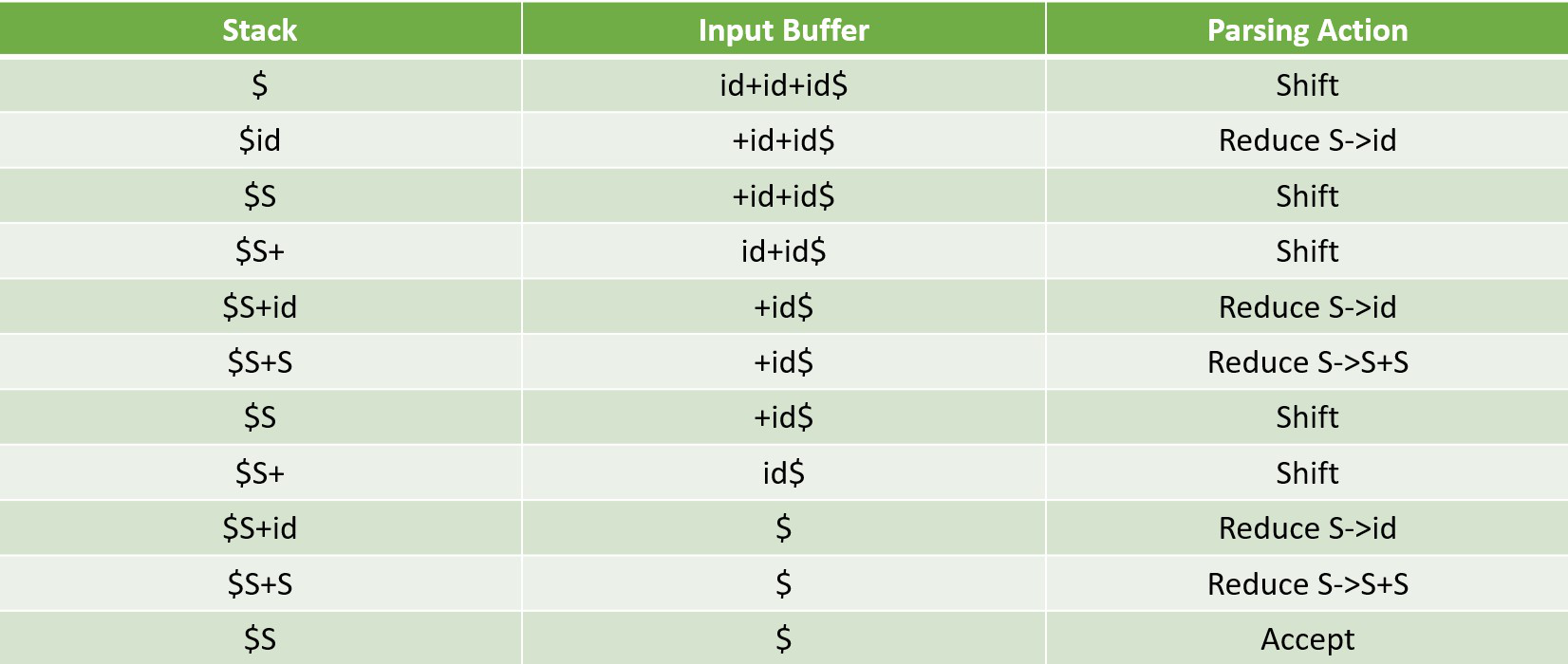
Example 1 – Consider the grammar
S –> S + S
S –> S * S
S –> id
Perform Shift Reduce parsing for input string “id + id + id”.
Example 2 – Consider the grammar
E –> 2E2
E –> 3E3
E –> 4
Perform Shift Reduce parsing for input string “32423”.
Example 3 – Consider the grammar
S –> ( L ) | a
L –> L , S | S
Perform Shift Reduce parsing for input string “( a, ( a, a ) ) “.
| Stack | Input Buffer | Parsing Action |
|---|
| $ | ( a , ( a , a ) ) $ | Shift |
| $ ( | a , ( a , a ) ) $ | Shift |
| $ ( a | , ( a , a ) ) $ | Reduce S → a |
| $ ( S | , ( a , a ) ) $ | Reduce L → S |
| $ ( L | , ( a , a ) ) $ | Shift |
| $ ( L , | ( a , a ) ) $ | Shift |
| $ ( L , ( | a , a ) ) $ | Shift |
| $ ( L , ( a | , a ) ) $ | Reduce S → a |
| $ ( L , ( S | , a ) ) $ | Reduce L → S |
| $ ( L , ( L | , a ) ) $ | Shift |
| $ ( L , ( L , | a ) ) $ | Shift |
| $ ( L , ( L , a | ) ) $ | Reduce S → a |
| $ ( L, ( L, S | ) ) $ | Reduce L →L, S |
| $ ( L, ( L | ) ) $ | Shift |
| $ ( L, ( L ) | ) $ | Reduce S → (L) |
| $ ( L, S | ) $ | Reduce L → L, S |
| $ ( L | ) $ | Shift |
| $ ( L ) | $ | Reduce S → (L) |
| $ S | $ | Accept |
Following is the implementation-
C++
#include <bits/stdc++.h>
using namespace std;
int z = 0, i = 0, j = 0, c = 0;
char a[16], ac[20], stk[15], act[10];
void check()
{
strcpy(ac,"REDUCE TO E -> ");
for(z = 0; z < c; z++)
{
if(stk[z] == '4')
{
printf("%s4", ac);
stk[z] = 'E';
stk[z + 1] = '\0';
printf("\n$%s\t%s$\t", stk, a);
}
}
for(z = 0; z < c - 2; z++)
{
if(stk[z] == '2' && stk[z + 1] == 'E' &&
stk[z + 2] == '2')
{
printf("%s2E2", ac);
stk[z] = 'E';
stk[z + 1] = '\0';
stk[z + 2] = '\0';
printf("\n$%s\t%s$\t", stk, a);
i = i - 2;
}
}
for(z = 0; z < c - 2; z++)
{
if(stk[z] == '3' && stk[z + 1] == 'E' &&
stk[z + 2] == '3')
{
printf("%s3E3", ac);
stk[z]='E';
stk[z + 1]='\0';
stk[z + 2]='\0';
printf("\n$%s\t%s$\t", stk, a);
i = i - 2;
}
}
return ;
}
int main()
{
printf("GRAMMAR is -\nE->2E2 \nE->3E3 \nE->4\n");
strcpy(a,"32423");
c=strlen(a);
strcpy(act,"SHIFT");
printf("\nstack \t input \t action");
printf("\n$\t%s$\t", a);
for(i = 0; j < c; i++, j++)
{
printf("%s", act);
stk[i] = a[j];
stk[i + 1] = '\0';
a[j]=' ';
printf("\n$%s\t%s$\t", stk, a);
check();
}
check();
if(stk[0] == 'E' && stk[1] == '\0')
printf("Accept\n");
else
printf("Reject\n");
}
|
C
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
int z = 0, i = 0, j = 0, c = 0;
char a[16], ac[20], stk[15], act[10];
void check()
{
strcpy(ac,"REDUCE TO E -> ");
for(z = 0; z < c; z++)
{
if(stk[z] == '4')
{
printf("%s4", ac);
stk[z] = 'E';
stk[z + 1] = '\0';
printf("\n$%s\t%s$\t", stk, a);
}
}
for(z = 0; z < c - 2; z++)
{
if(stk[z] == '2' && stk[z + 1] == 'E' &&
stk[z + 2] == '2')
{
printf("%s2E2", ac);
stk[z] = 'E';
stk[z + 1] = '\0';
stk[z + 2] = '\0';
printf("\n$%s\t%s$\t", stk, a);
i = i - 2;
}
}
for(z=0; z<c-2; z++)
{
if(stk[z] == '3' && stk[z + 1] == 'E' &&
stk[z + 2] == '3')
{
printf("%s3E3", ac);
stk[z]='E';
stk[z + 1]='\0';
stk[z + 1]='\0';
printf("\n$%s\t%s$\t", stk, a);
i = i - 2;
}
}
return ;
}
int main()
{
printf("GRAMMAR is -\nE->2E2 \nE->3E3 \nE->4\n");
strcpy(a,"32423");
c=strlen(a);
strcpy(act,"SHIFT");
printf("\nstack \t input \t action");
printf("\n$\t%s$\t", a);
for(i = 0; j < c; i++, j++)
{
printf("%s", act);
stk[i] = a[j];
stk[i + 1] = '\0';
a[j]=' ';
printf("\n$%s\t%s$\t", stk, a);
check();
}
check();
if(stk[0] == 'E' && stk[1] == '\0')
printf("Accept\n");
else
printf("Reject\n");
}
|
OutputGRAMMAR is -
E->2E2
E->3E3
E->4
stack input action
$ 32423$ SHIFT
$3 2423$ SHIFT
$32 423$ SHIFT
$324 23$ REDUCE TO E -> 4
$32E 23$ SHIFT
$32E2 3$ REDUCE TO E -> 2E2
$3E 3$ SHIFT
$3E3 $ REDUCE TO E -> 3E3
$E $ Accept
Advantages:
- Shift-reduce parsing is efficient and can handle a wide range of context-free grammars.
- It can parse a large variety of programming languages and is widely used in practice.
- It is capable of handling both left- and right-recursive grammars, which can be important in parsing certain programming languages.
- The parse table generated for shift-reduce parsing is typically small, which makes the parser efficient in terms of memory usage.
Disadvantages:
- Shift-reduce parsing has a limited lookahead, which means that it may miss some syntax errors that require a larger lookahead.
- It may also generate false-positive shift-reduce conflicts, which can require additional manual intervention to resolve.
- Shift-reduce parsers may have difficulty in parsing ambiguous grammars, where there are multiple possible parse trees for a given input sequence.
- In some cases, the parse tree generated by shift-reduce parsing may be more complex than other parsing techniques.