Code Generation and Optimization
Question 1
Which of the following macros can put a micro assembler into an infinite loop?
(i)
.MACRO M1 X .IF EQ, X ;if X=0 then M1 X + 1 .ENDC .IF NE X ;IF X≠0 then .WORD X ;address (X) is stored here .ENDC .ENDM(ii)
.MACRO M2 X .IF EQ X M2 X .ENDC .IF NE, X .WORD X+1 .ENDC .ENDM
Question 3
In a simplified computer the instructions are:
 The computer has only two registers, and OP is either ADD or SUB. Consider the following basic block:
The computer has only two registers, and OP is either ADD or SUB. Consider the following basic block:
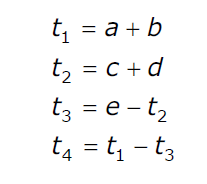 Assume that all operands are initially in memory. The final value of the computation should be in memory. What is the minimum number of MOV instructions in the code generated for this basic block?
Assume that all operands are initially in memory. The final value of the computation should be in memory. What is the minimum number of MOV instructions in the code generated for this basic block?
 The computer has only two registers, and OP is either ADD or SUB. Consider the following basic block:
The computer has only two registers, and OP is either ADD or SUB. Consider the following basic block:
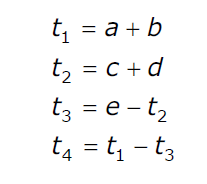 Assume that all operands are initially in memory. The final value of the computation should be in memory. What is the minimum number of MOV instructions in the code generated for this basic block?
Assume that all operands are initially in memory. The final value of the computation should be in memory. What is the minimum number of MOV instructions in the code generated for this basic block?Question 6
Consider the following C code segment.
for (i = 0, i<n; i++)
{
for (j=0; j<n; j++)
{
if (i%2)
{
x += (4*j + 5*i);
y += (7 + 4*j);
}
}
}
Which one of the following is false?
Question 7
Consider the grammar rule E → E1 - E2 for arithmetic expressions. The code generated is targeted to a CPU having a single user register. The subtraction operation requires the first operand to be in the register. If E1 and E2 do not have any common sub expression, in order to get the shortest possible code
Question 8
Consider the following statements.
- S1: The sequence of procedure calls corresponds to a preorder traversal of the activation tree.
- S2: The sequence of procedure returns corresponds to a postorder traversal of the activation tree.
Question 9
Consider the intermediate code given below:
1. i = 1 2. j = 1 3. t1 = 5 * i 4. t2 = t1 + j 5. t3 = 4 * t2 6. t4 = t3 7. a[t4] = –1 8. j = j + 1 9. if j <= 5 goto(3) 10. i = i + 1 11. if i < 5 goto(2)The number of nodes and edges in the control-flow-graph constructed for the above code, respectively, are
Question 10
Consider the following code segment.
x = u - t; y = x * v; x = y + w; y = t - z; y = x * y;The minimum number of total variables required to convert the above code segment to static single assignment form is Note : This question was asked as Numerical Answer Type.
There are 38 questions to complete.
Last Updated :
Take a part in the ongoing discussion
