Qubit Representation

Last Updated : 23 Nov, 2020

Similar to a bit in classical computing, a qubit is a basic building block of Quantum Computers. It represents the superposition of states 0 and 1. What we mean by superposition is that the given state is in a linear combination of state 0 and state 1.

It is a common misconception that qubit is in one state 0 or 1, we just don’t know until we measure it. However, qubit always exists in a state between 0 and 1 (inclusive), the act of measuring brings it to either of the states.

Matrix Representation : A qubit is represented as a complex vector of size 2. Generally represented as :

$\begin{bmatrix}\alpha\\\beta\end{bmatrix}$

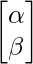
where

$\alpha, \beta$

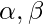
are amplitudes of states 0 and 1 respectively or we can say the probability to be in state 0 and 1 respectively. This vector is normalized i.e.

$| \alpha | ^2 +| \beta |^2 = 1$

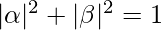
State 0 is represented as :

$\begin{bmatrix}1\\0\end{bmatrix}$

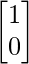
State 1 is represented as:

$\begin{bmatrix}0\\1\end{bmatrix}$

Quantum states |0> and |1> form orthogonal basis also called computational basis or canonical basis.

Dirac’s Notation : It is a shorthand notation for a qubit. A vector is represented using a ket.

$|0\rangle\ \ =\begin{bmatrix} 1 \\ 0 \end{bmatrix} and \ \ |1\rangle\ \ =\begin{bmatrix} 0 \\ 1 \end{bmatrix}$

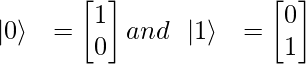
It also has a dual form written as:

$\langle0|\ \ =\begin{bmatrix} 1 \ 0 \end{bmatrix} and \ \ \langle1|\ \ =\begin{bmatrix} 0 \ 1 \end{bmatrix}$

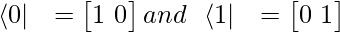
Hence, any arbitrary state can be represented as:

$|\Psi\rangle\ \ =\begin{bmatrix} \alpha \\ \beta \end{bmatrix} or \ |\Psi\rangle\ \ =\alpha |0\rangle + \beta |1\rangle$

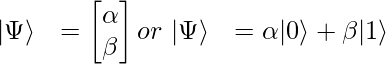
Some other symbols used are:

$|+\rangle\ \ = \frac{1}{\sqrt2}(|0\rangle+|1\rangle) \ \ and \ \ |-\rangle\ \ = \frac{1}{\sqrt2}(|0\rangle-|1\rangle)$

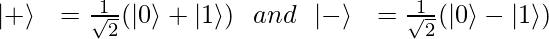
|+> and |-> are called Hadamard’s basis. These are also orthogonal to each other.

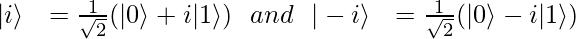$|i\rangle\ \ = \frac{1}{\sqrt2}(|0\rangle+i|1\rangle) \ \ and \ \ |-i\rangle\ \ = \frac{1}{\sqrt2}(|0\rangle-i|1\rangle)$ Bloch’s Representation : Bloch’s sphere is a geometric representation of quantum states where different points in the surface of the unit radius sphere represent various quantum states. A qubit can be represented in a 3D space as a vector of unit length connecting points in the surface of the Bloch’s sphere and it’s center.