Division Algorithm in Signed Magnitude Representation
Last Updated :
24 Jun, 2022
The Division of two fixed-point binary numbers in the signed-magnitude representation is done by the cycle of successive compare, shift, and subtract operations.
The binary division is easier than the decimal division because the quotient digit is either 0 or 1. Also, there is no need to estimate how many times the dividend or partial remainders adjust to the divisor.
Hardware Implementation :
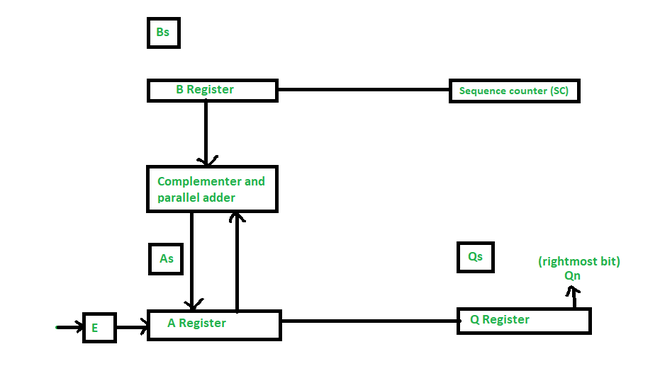
The hardware implementation in the division operation is identical to that required for multiplication and consists of the following components –
- Here, Registers B is used to store divisor, and the double-length dividend is stored in registers A and Q
- The information for the relative magnitude is given in E.
- A sequence Counter register (SC) is used to store the number of bits in the dividend.
Flowchart of Division :
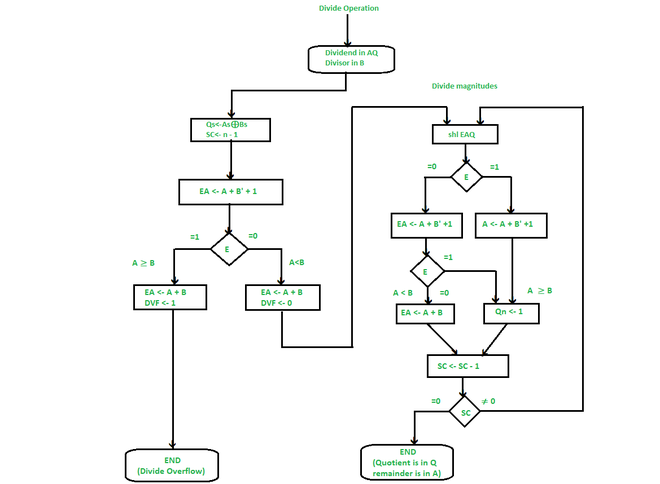
- Initially, the dividend is in A & Q and the divisor is in B.
- The sign of the result is transferred into Q, to be part of the quotient. Then a constant is set into the SC to specify the number of bits in the quotient.
- Since an operand must be saved with its sign, one bit of the word will be inhabited by the sign, and the magnitude will be composed of n -1 bits.
- The condition of divide-overflow is checked by subtracting the divisor in B from the half of the bits of the dividend stored in A. If A ≥ B, DVF is set and the operation is terminated before time. If A < B, no overflow condition occurs and so the value of the dividend is reinstated by adding B to A.
- The division of the magnitudes starts with the dividend in AQ to left in the high-order bit shifted into E.
(Note – If shifted a bit into E is equal to 1, and we know that EA > B as EA comprises a 1 followed by n -1 bits whereas B comprises only n -1 bits). In this case, B must be subtracted from EA, and 1 should insert into Q, for the quotient bit.
- If the shift-left operation (shl) inserts a 0 into E, the divisor is subtracted by adding its 2’s complement value and the carry is moved into E. If E = 1, it means that A ≥ B; thus, Q, is set to 1. If E = 0, it means that A < B, and the original number is reimposed by adding B into A.
- Now, this process is repeated with register A containing the partial remainder.
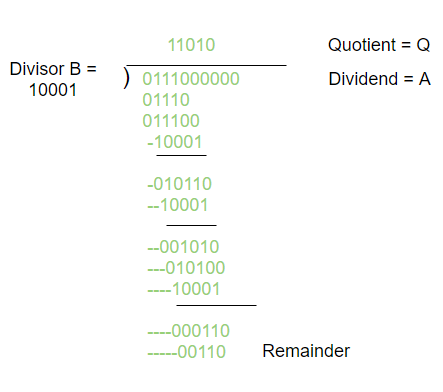
Example of a binary division using digital hardware:
Divisor B = 10001, Dividend A = 0111000000
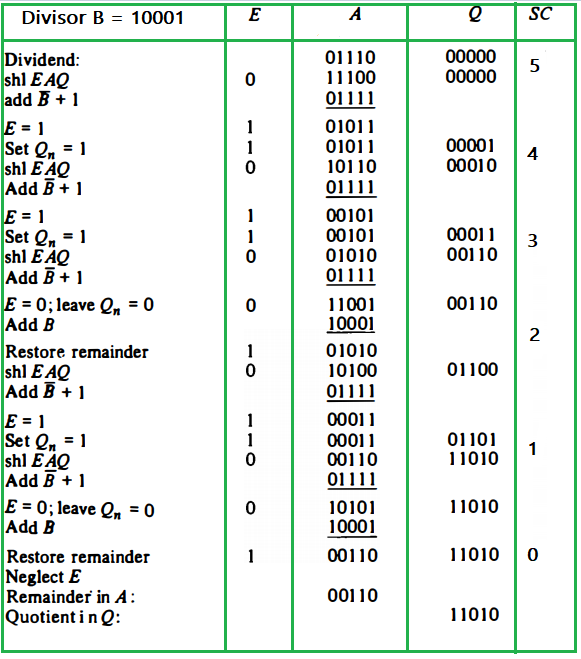
Final Remainder: 00110
Final Quotient: 11010
Now, what if the divisor is greater than or equal to the dividend. In this process, division overflow occurs. EA stores the value of A+B, there is no application of Q here as if the divisor is equal to dividend then Q might 1 and remainder is 0, else in every other condition the value of quotient 1 and remainder equals to the dividend.
Share your thoughts in the comments
Please Login to comment...