Multiplication Algorithm in Signed Magnitude Representation
Last Updated :
21 Aug, 2019
Multiplication of two fixed point binary number in signed magnitude representation is done with process of successive shift and add operation.

In the multiplication process we are considering successive bits of the multiplier, least significant bit first.
If the multiplier bit is 1, the multiplicand is copied down else 0’s are copied down.
The numbers copied down in successive lines are shifted one position to the left from the previous number.
Finally numbers are added and their sum form the product.
The sign of the product is determined from the sign of the multiplicand and multiplier. If they are alike, sign of the product is positive else negative.
Hardware Implementation :
Following components are required for the Hardware Implementation of multiplication algorithm :
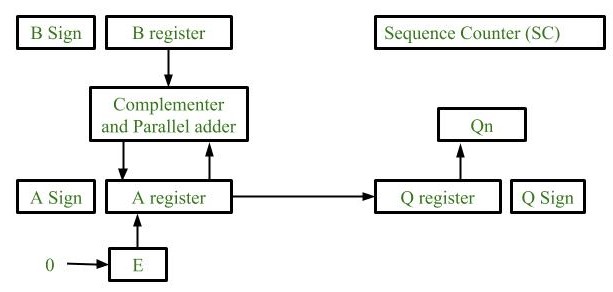
- Registers:
Two Registers B and Q are used to store multiplicand and multiplier respectively.
Register A is used to store partial product during multiplication.
Sequence Counter register (SC) is used to store number of bits in the multiplier.
- Flip Flop:
To store sign bit of registers we require three flip flops (A sign, B sign and Q sign).
Flip flop E is used to store carry bit generated during partial product addition.
- Complement and Parallel adder:
This hardware unit is used in calculating partial product i.e, perform addition required.
Flowchart of Multiplication:
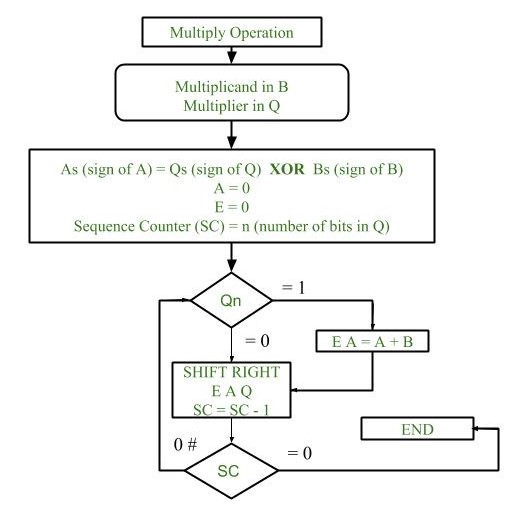
- Initially multiplicand is stored in B register and multiplier is stored in Q register.
- Sign of registers B (Bs) and Q (Qs) are compared using XOR functionality (i.e., if both the signs are alike, output of XOR operation is 0 unless 1) and output stored in As (sign of A register).
Note: Initially 0 is assigned to register A and E flip flop. Sequence counter is initialized with value n, n is the number of bits in the Multiplier.
- Now least significant bit of multiplier is checked. If it is 1 add the content of register A with Multiplicand (register B) and result is assigned in A register with carry bit in flip flop E. Content of E A Q is shifted to right by one position, i.e., content of E is shifted to most significant bit (MSB) of A and least significant bit of A is shifted to most significant bit of Q.
- If Qn = 0, only shift right operation on content of E A Q is performed in a similar fashion.
- Content of Sequence counter is decremented by 1.
- Check the content of Sequence counter (SC), if it is 0, end the process and the final product is present in register A and Q, else repeat the process.
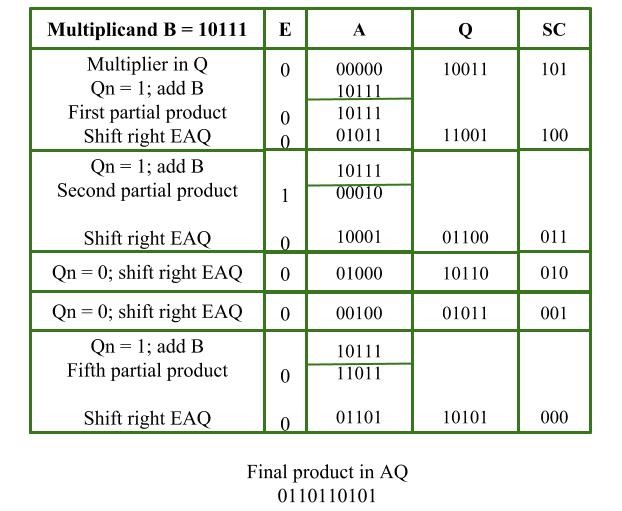
Example:
Multiplicand = 10111
Multiplier = 10011
Share your thoughts in the comments
Please Login to comment...