Python Program to find transpose of a matrix

Transpose of a matrix is obtained by changing rows to columns and columns to rows. In other words, transpose of A[][] is obtained by changing A[i][j] to A[j][i]. 

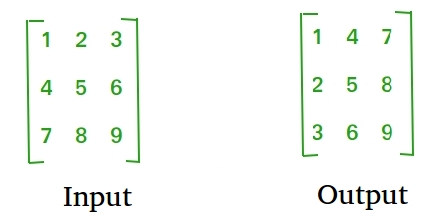
For Square Matrix: The below program finds transpose of A[][] and stores the result in B[][], we can change N for different dimension. 

Python3

# Python3 Program to find
# transpose of a matrix

N = 4

# This function stores
# transpose of A[][] in B[][]

def transpose(A,B):

 for i in range(N):
  for j in range(N):
   B[i][j] = A[j][i]

# driver code
A = [ [1, 1, 1, 1],
 [2, 2, 2, 2],
 [3, 3, 3, 3],
 [4, 4, 4, 4]]


B = A[:][:] # To store result

transpose(A, B)

print("Result matrix is")
for i in range(N):
 for j in range(N):
  print(B[i][j], " ", end='')
 print()

# This code is contributed by Anant Agarwal.

Output:

Result matrix is
1  2  3  4  
2  2  3  4  
3  3  3  4  
4  4  4  4

Time Complexity: O(n²)
Auxiliary Space: O(n²)

For Rectangular Matrix: The below program finds transpose of A[][] and stores the result in B[][]. 

Python3

# Python3 Program to find
# transpose of a matrix

M = 3
N = 4

# This function stores
# transpose of A[][] in B[][]

def transpose(A, B):

 for i in range(N):
  for j in range(M):
   B[i][j] = A[j][i]

# driver code
A = [ [1, 1, 1, 1],
 [2, 2, 2, 2],
 [3, 3, 3, 3]]


# To store result
B = [[0 for x in range(M)] for y in range(N)]

transpose(A, B)

print("Result matrix is")
for i in range(N):
 for j in range(M):
  print(B[i][j], " ", end='')
 print()

Output:

Result matrix is
1  2  3  
1  2  3  
1  2  3  
1  2  3

Time Complexity: O(n*m)
Auxiliary Space: O(n*m)

In-Place for Square Matrix:

Python3

# Python3 Program to find
# transpose of a matrix

N = 4

# Finds transpose of A[][] in-place
def transpose(A):

 for i in range(N):
  for j in range(i+1, N):
   A[i][j], A[j][i] = A[j][i], A[i][j]

# driver code
A = [ [1, 1, 1, 1],
 [2, 2, 2, 2],
 [3, 3, 3, 3],
 [4, 4, 4, 4]]

transpose(A)

print("Modified matrix is")
for i in range(N):
 for j in range(N):
  print(A[i][j], " ", end='')
 print()

# This code is contributed by Anant Agarwal.

Output:

Modified matrix is
1  2  3  4  
1  2  3  4  
1  2  3  4  
1  2  3  4

Time Complexity: O(n²)
Auxiliary Space: O(1)

Please refer complete article on Program to find transpose of a matrix for more details!