C++ Program To Find Transpose of a Matrix

Transpose of a matrix is obtained by changing rows to columns and columns to rows. In other words, the transpose of A[][] is obtained by changing A[i][j] to A[j][i].

Example:

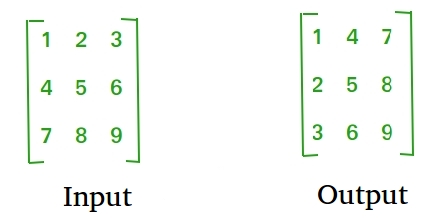
1. For Square Matrix 

The below program finds the transpose of A[][] and stores the result in B[][], we can change N for a different dimension.  

C++

// C++ Program to find the transpose
// of a matrix
#include <bits/stdc++.h>
using namespace std;
#define N 4

// This function stores transpose
// of A[][] in B[][]
void transpose(int A[][N],
               int B[][N])
{
    int i, j;
    for (i = 0; i < N; i++)
        for (j = 0; j < N; j++)
            B[i][j] = A[j][i];
}

// Driver code
int main()
{
    int A[N][N] = {{1, 1, 1, 1},
                   {2, 2, 2, 2},
                   {3, 3, 3, 3},
                   {4, 4, 4, 4}};

    int B[N][N], i, j;

    transpose(A, B);

    cout << "Result matrix is \n";
    for (i = 0; i < N; i++)
    {
        for (j = 0; j < N; j++)
           cout << " " << B[i][j];
        cout <<"\n";
    }
    return 0;
}

Output

Result matrix is 
 1 2 3 4
 1 2 3 4
 1 2 3 4
 1 2 3 4

The complexity of the above method

Time Complexity: O(N*N) as two nested loops are running.

Space Complexity: O(N*N) as 2d array is created to store transpose.

2. For Rectangular Matrix

The below program finds the transpose of A[][] and stores the result in B[][]. 

C++

// C++ program to find transpose
// of a matrix
#include <bits/stdc++.h>
using namespace std;
#define M 3
#define N 4

// This function stores transpose
// of A[][] in B[][]
void transpose(int A[][N], int B[][M])
{
    int i, j;
    for(i = 0; i < N; i++)
        for(j = 0; j < M; j++)
            B[i][j] = A[j][i];
}

// Driver code
int main()
{
    int A[M][N] = {{1, 1, 1, 1},
                   {2, 2, 2, 2},
                   {3, 3, 3, 3}};

    // Note dimensions of B[][]
    int B[N][M], i, j;

    transpose(A, B);

    cout << "Result matrix is \n";
    for(i = 0; i < N; i++)
    {
        for(j = 0; j < M; j++)
            cout << " " << B[i][j];

        cout << "\n";
    }
    return 0;
}

Output

Result matrix is 
 1 2 3
 1 2 3
 1 2 3
 1 2 3

The complexity of the above method

Time Complexity: O(N*M) as two nested loops are running.

Space Complexity: O(N*M) as 2d array is created to store transpose.

3. In-Place for Square Matrix

Below is the implementation of the method:

C++

// C++ program to implement
// the above approach
#include <bits/stdc++.h>
using namespace std;

#define N 4

// Converts A[][] to its transpose
void transpose(int A[][N])
{
    for (int i = 0; i < N; i++)
        for (int j = i+1; j < N; j++)
            swap(A[i][j], A[j][i]);
}

// Driver code
int main()
{
    int A[N][N] = {{1, 1, 1, 1},
                   {2, 2, 2, 2},
                   {3, 3, 3, 3},
                   {4, 4, 4, 4}};

    transpose(A);

    printf("Modified matrix is \n");
    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < N; j++)
           printf("%d ", A[i][j]);
        printf("\n");
    }

    return 0;
}

Output

Modified matrix is 
1 2 3 4 
1 2 3 4 
1 2 3 4 
1 2 3 4 

The complexity of the above method

Time complexity: O(n)

• Transpose has a time complexity of O(n + m), where n is the number of columns and m is the number of non-zero elements in the matrix. 
• The computational time for transposing of a matrix using an identity matrix as a reference matrix is O(m*n). 
• Suppose, if the given matrix is a square matrix, the running time will be O(n²).

Auxiliary space: O(1).