Python – 68-95-99.7 rule in Statistics
Last Updated :
01 Sep, 2021
The Empirical Rule(also called the 68-95-99.7 Rule or the Three Sigma Rule) states that for any normal distribution, we have the following observations :
- 68% of the observed values lie between 1 standard deviation around the mean :
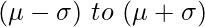
- 95% of the observed values lie between 2 standard deviations around the mean :
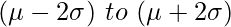
- 99.7% of the observed values lie between 3 standard deviation around the mean :
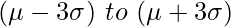
Below is a standard normal distribution graph with (mean = 0 and standard deviation = 1), illustrating the Empirical Rule.
We, can verify this using functions provided by Python’s SciPy module.
We can use the
cdf() function of the
scipy.stats.norm module to calculate the cumulative probability(area under a distribution curve).
Syntax : cdf(x, mean, SD)
Parameters :
- x : value up to which cumulative probability is to be calculated
- mean : mean of the distribution
- SD : standard deviation of the distribution
Below is the implementation :
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
mean = 0
SD = 1
one_sd = norm.cdf(SD, mean, SD) - norm.cdf(-SD, mean, SD)
two_sd = norm.cdf(2 * SD, mean, SD) - norm.cdf(-2 * SD, mean, SD)
three_sd = norm.cdf(3 * SD, mean, SD) - norm.cdf(-3 * SD, mean, SD)
print("Fraction of values within one SD =", one_sd)
print("Fraction of values within two SD =", two_sd)
print("Fraction of values within three SD =", three_sd)
|
Output :
Fraction of values within one SD = 0.6826894921370859
Fraction of values within two SD = 0.9544997361036416
Fraction of values within three SD = 0.9973002039367398
Hence, we see that the fraction of values are almost equal to 0.65, 0.95 and 0.997. Thus, the empirical Rule is verified.
Share your thoughts in the comments
Please Login to comment...