Program to check if N is a Centered Hexadecagonal Number
Last Updated :
22 Sep, 2022
Given a number N, the task is to check if N is a Centered Hexadecagonal Number or not. If the number N is a Centered Hexadecagonal Number then print “Yes” else print “No”.
Centered Hexadecagonal Number represents a dot in the centre and other dots around it in successive Hexadecagonal(16 sided polygon) layers… The first few Centered Hexadecagonal Numbers are 1, 17, 49, 97, 161, 241 …
Examples:
Input: N = 17
Output: Yes
Explanation:
Second Centered hexadecagonal number is 17.
Input: N = 20
Output: No
Approach:
1. The Kth term of the Centered Hexadecagonal Number is given as

2. As we have to check that the given number can be expressed as a Centered Hexadecagonal Number or not. This can be checked as:
=> 
=> 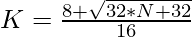
3. If the value of K calculated using the above formula is an integer, then N is a Centered Hexadecagonal Number.
4. Else the number N is not a Centered Hexadecagonal Number.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool isCenteredhexadecagonal(int N)
{
float n
= (8 + sqrt(32 * N + 32))
/ 16;
return (n - (int)n) == 0;
}
int main()
{
int N = 17;
if (isCenteredhexadecagonal(N)) {
cout << "Yes";
}
else {
cout << "No";
}
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG {
static boolean isCenteredhexadecagonal(int N)
{
double n = (8 + Math.sqrt(32 * N + 32)) / 16;
return (n - (int)n) == 0;
}
public static void main(String[] args)
{
int N = 17;
if (isCenteredhexadecagonal(N))
{
System.out.println("Yes");
}
else
{
System.out.println("No");
}
}
}
|
Python3
import numpy as np
def isCenteredhexadecagonal(N):
n = (8 + np.sqrt(32 * N + 32)) / 16
return (n - int(n)) == 0
N = 17
if (isCenteredhexadecagonal(N)):
print ("Yes")
else:
print ("No")
|
C#
using System;
class GFG {
static bool isCenteredhexadecagonal(int N)
{
double n = (8 + Math.Sqrt(32 * N + 32)) / 16;
return (n - (int)n) == 0;
}
public static void Main(string[] args)
{
int N = 17;
if (isCenteredhexadecagonal(N))
{
Console.Write("Yes");
}
else
{
Console.Write("No");
}
}
}
|
Javascript
<script>
function isCenteredhexadecagonal( N)
{
let n
= (8 + Math.sqrt(32 * N + 32))
/ 16;
return (n - parseInt(n)) == 0;
}
let N = 17;
if (isCenteredhexadecagonal(N)) {
document.write( "Yes");
}
else {
document.write( "No");
}
</script>
|
Time Complexity: O(logN), for using inbuilt sqrt function.
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...