Probability of distributing M items among X bags such that first bag contains N items
Last Updated :
02 Sep, 2022
Given three integers N, M, X. The task is to find the probability of distributing M items among X bags such that first bag contains N items
Examples:
Input : M = 7, X =3, N = 3
Output : 0.2
The Number of ways to keep 7 items in 3 bags is 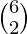 .
.
The Number of ways to keep 4 items in 2 bags is 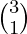 . As the first bag contains 3 items.
. As the first bag contains 3 items.
The probability is 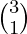 /
/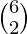
Input : M = 9, X = 3, N = 4
Output : 0.142857
Approach :
In general, the Number of ways to place N items in K bags is 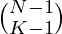 .
.
- The Number of ways to keep M items in X bags is
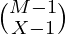 .
. - The Number of ways to keep (M-N) items in (X-1) bags is
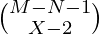 . As the first bag contains N items.
. As the first bag contains N items. - The probability is
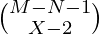 /
/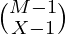 .
.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int factorial(int n)
{
if (n <= 1)
return 1;
return n * factorial(n - 1);
}
int nCr(int n, int r)
{
return factorial(n) / (factorial(r) * factorial(n - r));
}
float Probability(int M, int N, int X)
{
return (float)(nCr(M - N - 1, X - 2) /
(nCr(M - 1, X - 1) * 1.0));
}
int main()
{
int M = 9, X = 3, N = 4;
cout << Probability(M, N, X);
return 0;
}
|
Java
class GFG
{
public static int factorial(int n)
{
if (n <= 1)
return 1;
return n * factorial(n - 1);
}
public static int nCr(int n, int r)
{
return factorial(n) / (factorial(r) * factorial(n - r));
}
public static float Probability(int M, int N, int X)
{
return (float) (nCr(M - N - 1, X - 2) / (nCr(M - 1, X - 1) * 1.0));
}
public static void main(String[] args)
{
int M = 9, X = 3, N = 4;
System.out.println(Probability(M, N, X));
}
}
|
Python3
def factorial(n) :
if (n <= 1) :
return 1;
return n * factorial(n - 1);
def nCr(n, r) :
return (factorial(n) / (factorial(r) *
factorial(n - r)));
def Probability(M, N, X) :
return float(nCr(M - N - 1, X - 2) /
(nCr(M - 1, X - 1) * 1.0));
if __name__ == "__main__" :
M = 9; X = 3; N = 4;
print(Probability(M, N, X));
|
C#
using System;
class GFG
{
static int factorial(int n)
{
if (n <= 1)
return 1;
return n * factorial(n - 1);
}
static int nCr(int n, int r)
{
return factorial(n) / (factorial(r) * factorial(n - r));
}
static float Probability(int M, int N, int X)
{
return (float) (nCr(M - N - 1, X - 2) / (nCr(M - 1, X - 1) * 1.0));
}
static void Main()
{
int M = 9, X = 3, N = 4;
Console.WriteLine(Probability(M, N, X));
}
}
|
Javascript
<script>
function factorial( n)
{
if (n <= 1)
return 1;
return n * factorial(n - 1);
}
function nCr( n, r)
{
return factorial(n) / (factorial(r) * factorial(n - r));
}
function Probability(M,N,X)
{
return parseFloat(nCr(M - N - 1, X - 2) / (nCr(M - 1, X - 1) * 1.0));
}
let M = 9, X = 3, N = 4;
document.write(Probability(M, N, X).toFixed(6));
</script>
|
Time Complexity: O(n), time taken by the algorithm is linear as the recursion runs for n times
Auxiliary Space: O(n) due to the recursive call stack, In worst case the stack will contain all recursive calls till n becomes 0 hence the space taken by the algorithm is linear
Share your thoughts in the comments
Please Login to comment...