Vertical order traversal of Binary Tree using Map
Last Updated :
19 Apr, 2023
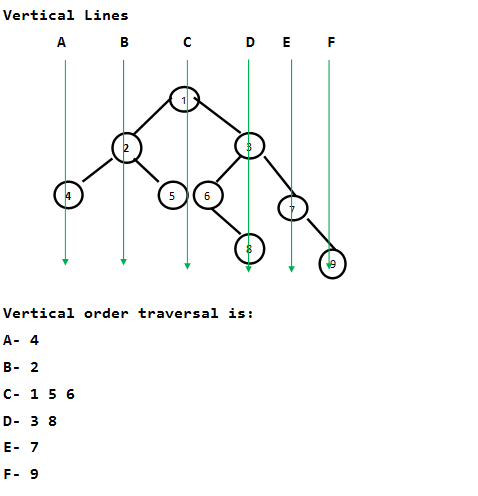
Given a binary tree, print it vertically. The following examples illustrate the vertical order traversal.
Examples:
Input: 1
/ \
2 3
/ \ / \
4 5 6 7
/ \
8 9
Output:
4
2
1 5 6
3 8
7
9
Vertical order traversal of the binary tree using Self Balancing BSTs:
To solve the problem follow the below idea:
We need to check the Horizontal Distances from the root for all nodes. If two nodes have the same Horizontal Distance (HD), then they are on the same vertical line. The idea of HD is simple. HD for root is 0, a right edge (edge connecting to right subtree) is considered as +1 horizontal distance and a left edge is considered as -1 horizontal distance.
Follow the below steps to solve the problem:
- Do a preorder traversal of the given Binary Tree.
- While traversing the tree, we can recursively calculate HDs. We initially pass the horizontal distance as 0 for the root.
- For the left subtree, we pass the Horizontal Distance as the Horizontal distance of the root minus 1.
- For the right subtree, we pass the Horizontal Distance as the Horizontal Distance of the root plus 1.
- For every HD value, we maintain a list of nodes in a hash map. Whenever we see a node in traversal, we go to the hash map entry and add the node to the hash map using HD as a key in a map.
Below is the implementation of the above approach, thanks to Chirag for providing the below C++ implementation:
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int key;
Node *left, *right;
};
struct Node* newNode(int key)
{
struct Node* node = new Node;
node->key = key;
node->left = node->right = NULL;
return node;
}
void getVerticalOrder(Node* root, int hd,
map<int, vector<int> >& m)
{
if (root == NULL)
return;
m[hd].push_back(root->key);
getVerticalOrder(root->left, hd - 1, m);
getVerticalOrder(root->right, hd + 1, m);
}
void printVerticalOrder(Node* root)
{
map<int, vector<int> > m;
int hd = 0;
getVerticalOrder(root, hd, m);
map<int, vector<int> >::iterator it;
for (it = m.begin(); it != m.end(); it++) {
for (int i = 0; i < it->second.size(); ++i)
cout << it->second[i] << " ";
cout << endl;
}
}
int main()
{
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
root->right->left->right = newNode(8);
root->right->right->right = newNode(9);
cout << "Vertical order traversal is \n";
printVerticalOrder(root);
return 0;
}
|
Java
import java.util.Map.Entry;
import java.util.TreeMap;
import java.util.Vector;
public class VerticalOrderBtree {
static class Node {
int key;
Node left;
Node right;
Node(int data)
{
key = data;
left = null;
right = null;
}
}
static void
getVerticalOrder(Node root, int hd,
TreeMap<Integer, Vector<Integer> > m)
{
if (root == null)
return;
Vector<Integer> get = m.get(hd);
if (get == null) {
get = new Vector<>();
get.add(root.key);
}
else
get.add(root.key);
m.put(hd, get);
getVerticalOrder(root.left, hd - 1, m);
getVerticalOrder(root.right, hd + 1, m);
}
static void printVerticalOrder(Node root)
{
TreeMap<Integer, Vector<Integer> > m
= new TreeMap<>();
int hd = 0;
getVerticalOrder(root, hd, m);
for (Entry<Integer, Vector<Integer> > entry :
m.entrySet()) {
System.out.println(entry.getValue());
}
}
public static void main(String[] args)
{
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.right.left.right = new Node(8);
root.right.right.right = new Node(9);
System.out.println("Vertical Order traversal is");
printVerticalOrder(root);
}
}
|
Python3
class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
def getVerticalOrder(root, hd, m):
if root is None:
return
try:
m[hd].append(root.key)
except:
m[hd] = [root.key]
getVerticalOrder(root.left, hd-1, m)
getVerticalOrder(root.right, hd+1, m)
def printVerticalOrder(root):
m = dict()
hd = 0
getVerticalOrder(root, hd, m)
for index, value in enumerate(sorted(m)):
for i in m[value]:
print(i, end=" ")
print()
if __name__ == '__main__':
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
root.right.left.right = Node(8)
root.right.right.right = Node(9)
print("Vertical order traversal is")
printVerticalOrder(root)
|
C#
using System;
using System.Collections.Generic;
public class VerticalOrderBtree {
public class Node {
public int key;
public Node left;
public Node right;
public Node(int data)
{
key = data;
left = null;
right = null;
}
}
static void
getVerticalOrder(Node root, int hd,
SortedDictionary<int, List<int> > m)
{
if (root == null)
return;
List<int> get = new List<int>();
if (m.ContainsKey(hd))
get.AddRange(m[hd]);
if (get == null) {
get = new List<int>();
get.Add(root.key);
}
else
get.Add(root.key);
m[hd] = get;
getVerticalOrder(root.left, hd - 1, m);
getVerticalOrder(root.right, hd + 1, m);
}
static void printVerticalOrder(Node root)
{
SortedDictionary<int, List<int> > m
= new SortedDictionary<int, List<int> >();
int hd = 0;
getVerticalOrder(root, hd, m);
foreach(KeyValuePair<int, List<int> > entry in m)
{
foreach(int v in entry.Value)
Console.Write(v + " ");
Console.WriteLine();
}
}
public static void Main(String[] args)
{
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.right.left.right = new Node(8);
root.right.right.right = new Node(9);
Console.WriteLine("Vertical Order traversal is");
printVerticalOrder(root);
}
}
|
Javascript
class Node {
constructor(val){
this.key = val;
this.left = null;
this.right = null;
}
}
function getVerticalOrder(root, hd, m)
{
if (root == null)
return;
if((hd in m) == false){
m[hd] = new Array();
}
m[hd].push(root.key);
getVerticalOrder(root.left, hd - 1, m);
getVerticalOrder(root.right, hd + 1, m);
}
function sortFunction(a, b) {
if (a[0] === b[0]) {
return 0;
}
else {
return (a[0] < b[0]) ? -1 : 1;
}
}
function printVerticalOrder(root)
{
let m = {};
let hd = 0;
getVerticalOrder(root, hd, m);
let x = new Array();
for (const key in m) {
let y = new Array();
y.push(parseInt(key));
for(let i = 0; i < m[key].length; i++){
y.push(m[key][i]);
}
x.push(y);
}
x.sort(sortFunction);
for(let i = 0; i < x.length; i++){
for(let j = 0; j < x[i].length; j++){
if(j == 0) continue;
document.write(x[i][j] + " ");
}
document.write("\n");
}
}
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.right.left.right = new Node(8);
root.right.right.right = new Node(9);
console.log("Vertical order traversal is \n");
printVerticalOrder(root);
|
Output
Vertical order traversal is
4
2
1 5 6
3 8
7
9
Time Complexity: O(N log N). The hashing based solution can be considered as O(N) under the assumption that we have a good hashing function that allows insertion and retrieval operations in O(1) time. In the above C++ implementation, map of STL is used. map in STL is typically implemented using a Self-Balancing Binary Search Tree where all operations take O(Log N) time.
Auxiliary Space: O(N)
Note: The above solution may not print nodes in the same vertical order as they appear in the tree.
For example, the above program prints 12 before 9. See this for a sample run.
1
/ \
2 3
/ \ / \
4 5 6 7
/ \
8 9
/ \
10 11
\
12
Refer below post for a level order traversal-based solution. The below post makes sure that nodes of a vertical line are printed in the same order as they appear in the tree: Print a Binary Tree in Vertical Order | Set 3 (Using Level Order Traversal)
Print vertical order traversal of the binary tree in the same order as they appear:
To solve the problem follow the below idea:
We can also maintain the order of nodes in the same vertical order as they appear in the tree. Nodes having the same horizontal distance will print according to level order.
For example, In below diagram 9 and 12 have the same horizontal distance. We can make sure that if a node like 12 comes below in the same vertical line, it is printed after a node like 9
Idea: Instead of using horizontal distance as a key in the map, we will use horizontal distance + vertical distance as the key. We know that the number of nodes can’t be more than the integer range in a binary tree.
We will use the first 30 bits of the key for horizontal distance [MSB to LSB] and will use the 30 next bits for vertical distance. Thus keys will be stored in the map as per our requirement.
Follow the below steps to solve the problem:
- Declare a map to store the value of nodes at each level
- If the root is null then return from the function(Base case)
- Create an integer val and set its value to horizontal distance << 30 OR vertical distance
- Push root->data in the map using val as the key
- Recur for root->left and root->right with horizontal distance – 1, vertical distance + 1 and horizontal distance + 1, vertical distance -1 respectively
- Print the solution using map
Below is the implementation of the above approach:
C++14
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
Node *left, *right;
};
struct Node* newNode(int data)
{
struct Node* node = new Node;
node->data = data;
node->left = node->right = NULL;
return node;
}
void preOrderTraversal(Node* root, long long int hd,
long long int vd,
map<long long int, vector<int> >& m)
{
if (!root)
return;
long long val = hd << 30 | vd;
m[val].push_back(root->data);
preOrderTraversal(root->left, hd - 1, vd + 1, m);
preOrderTraversal(root->right, hd + 1, vd + 1, m);
}
void verticalOrder(Node* root)
{
map<long long int, vector<int> > mp;
preOrderTraversal(root, 0, 1, mp);
int prekey = INT_MAX;
map<long long int, vector<int> >::iterator it;
for (it = mp.begin(); it != mp.end(); it++) {
if (prekey != INT_MAX
&& (it->first >> 30) != prekey) {
cout << endl;
}
prekey = it->first >> 30;
for (int j = 0; j < it->second.size(); j++)
cout << it->second[j] << " ";
}
}
int main()
{
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
root->right->left->right = newNode(8);
root->right->right->right = newNode(9);
cout << "Vertical order traversal :- " << endl;
verticalOrder(root);
return 0;
}
|
Java
import java.util.Map.Entry;
import java.util.TreeMap;
import java.util.Vector;
public class VerticalOrderBtree {
static class Node {
int data;
Node left;
Node right;
Node(int key)
{
data = key;
left = null;
right = null;
}
}
static void
preOrderTraversal(Node root, long hd, long vd,
TreeMap<Long, Vector<Integer> > m)
{
if (root == null)
return;
long val = hd << 30 | vd;
if (m.get(val) != null)
m.get(val).add(root.data);
else {
Vector<Integer> v = new Vector<Integer>();
v.add(root.data);
m.put(val, v);
}
preOrderTraversal(root.left, hd - 1, vd + 1, m);
preOrderTraversal(root.right, hd + 1, vd + 1, m);
}
static void verticalOrder(Node root)
{
TreeMap<Long, Vector<Integer> > mp
= new TreeMap<>();
preOrderTraversal(root, 0, 1, mp);
int prekey = Integer.MAX_VALUE;
for (Entry<Long, Vector<Integer> > entry :
mp.entrySet()) {
if (prekey != Integer.MAX_VALUE
&& (entry.getKey() >> 30) != prekey) {
System.out.println();
}
prekey = (int)(entry.getKey() >> 30);
for (int x : entry.getValue())
System.out.print(x + " ");
}
}
public static void main(String[] args)
{
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.right.left.right = new Node(8);
root.right.right.right = new Node(9);
System.out.println("Vertical Order traversal :- ");
verticalOrder(root);
}
}
|
Python3
import sys
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def preOrderTraversal(root, hd, vd, m):
if not root:
return
val = hd << 30 | vd
if val in m:
m[val].append(root.data)
else:
m[val] = [root.data]
preOrderTraversal(root.left, hd-1, vd+1, m)
preOrderTraversal(root.right, hd+1, vd+1, m)
def verticalOrder(root):
mp = dict()
preOrderTraversal(root, 0, 0, mp)
prekey = sys.maxsize
for i in sorted(mp.keys()):
if (prekey != sys.maxsize) and (i >> 30 != prekey):
print()
prekey = i >> 30
for j in mp[i]:
print(j, end=" ")
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
root.right.left.right = Node(8)
root.right.right.right = Node(9)
print("Vertical order traversal :- ")
verticalOrder(root)
|
C#
using System;
using System.Collections.Generic;
public class VerticalOrderBtree {
public class Node {
public int data;
public Node left;
public Node right;
public Node(int val)
{
data = val;
left = null;
right = null;
}
}
static void
preOrderTraversal(Node root, long hd, long vd,
SortedDictionary<long, List<int> > m)
{
if (root == null)
return;
long val = hd << 30 | vd;
if (m.ContainsKey(val) == true)
m[val].Add(root.data);
else {
List<int> v = new List<int>();
v.Add(root.data);
m.Add(val, v);
}
preOrderTraversal(root.left, hd - 1, vd + 1, m);
preOrderTraversal(root.right, hd + 1, vd + 1, m);
}
static void verticalOrder(Node root)
{
SortedDictionary<long, List<int> > mp
= new SortedDictionary<long, List<int> >();
preOrderTraversal(root, 0, 1, mp);
int prekey = Int32.MaxValue;
foreach(KeyValuePair<long, List<int> > entry in mp)
{
if (prekey != Int32.MaxValue
&& (entry.Key >> 30) != prekey) {
Console.WriteLine();
}
prekey = (int)entry.Key >> 30;
foreach(int v in entry.Value)
Console.Write(v + " ");
}
}
public static void Main(String[] args)
{
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.right.left.right = new Node(8);
root.right.right.right = new Node(9);
Console.WriteLine("Vertical Order traversal :- ");
verticalOrder(root);
}
}
|
Javascript
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
function preOrderTraversal(root, hd, vd, m) {
if (!root) return;
const val = BigInt(hd << 30n | vd);
if (!m.has(val)) {
m.set(val, []);
}
m.get(val).push(root.data);
preOrderTraversal(root.left, hd - 1n, vd + 1n, m);
preOrderTraversal(root.right, hd + 1n, vd + 1n, m);
}
function verticalOrder(root) {
const mp = new Map();
preOrderTraversal(root, 0n, 1n, mp);
let prekey = BigInt(Number.MAX_SAFE_INTEGER);
for (const [key, value] of [...mp.entries()].sort((a, b) => {
if (a[0] < b[0]) return -1;
if (a[0] > b[0]) return 1;
return 0;
})) {
if (prekey !== (key >> 30n)) {
console.log();
}
prekey = key >> 30n;
process.stdout.write(value.join(" ") + " ");
}
}
const root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.right.left.right = new Node(8);
root.right.right.right = new Node(9);
process.stdout.write("Vertical order traversal :- ");
verticalOrder(root);
|
Output
Vertical order traversal :-
4
2
1 5 6
3 8
7
9
Time Complexity: O(N Log N)
Auxiliary Space: O(N)
Vertical order traversal of the binary tree using computeIfAbsent method in Java:
We can write the code in a more concise way, by using computeIfAbsent method of the map in java and by using a treemap for natural sorting based upon keys.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* left;
Node* right;
Node(int item)
{
data = item;
left = right = NULL;
}
};
class BinaryTree {
public:
Node* root;
class Values {
public:
int max, min;
};
void verticalOrder(Node* node)
{
Values val;
map<int, vector<int> > mp;
findHorizontalDistance(node, &val, &val, 0, mp);
for (auto list : mp) {
for (auto element : list.second) {
cout << element << " ";
}
cout << endl;
}
}
void findHorizontalDistance(Node* node, Values* min,
Values* max, int hd,
map<int, vector<int> >& mp)
{
if (node == NULL)
return;
if (hd < min->min)
min->min = hd;
if (hd > max->max)
max->max = hd;
mp[hd].push_back(node->data);
findHorizontalDistance(node->left, min, max, hd - 1,
mp);
findHorizontalDistance(node->right, min, max,
hd + 1, mp);
}
};
int main()
{
BinaryTree tree;
tree.root = new Node(1);
tree.root->left = new Node(2);
tree.root->right = new Node(3);
tree.root->left->left = new Node(4);
tree.root->left->right = new Node(5);
tree.root->right->left = new Node(6);
tree.root->right->right = new Node(7);
tree.root->right->left->right = new Node(8);
tree.root->right->right->right = new Node(9);
cout << "vertical order traversal is :\n";
tree.verticalOrder(tree.root);
return 0;
}
|
Java
import java.util.ArrayList;
import java.util.List;
import java.util.Map;
import java.util.TreeMap;
class Node {
int data;
Node left, right;
Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree {
Node root;
class Values {
int max, min;
}
public void verticalOrder(Node node)
{
Values val = new Values();
Map<Integer, List<Integer> > map
= new TreeMap<Integer, List<Integer> >();
findHorizontalDistance(node, val, val, 0, map);
for (List<Integer> list : map.values()) {
System.out.println(list);
}
}
public void
findHorizontalDistance(Node node, Values min,
Values max, int hd,
Map<Integer, List<Integer> > map)
{
if (node == null)
return;
if (hd < min.min)
min.min = hd;
if (hd > max.max)
max.max = hd;
map.computeIfAbsent(hd,
k -> new ArrayList<Integer>())
.add(node.data);
findHorizontalDistance(node.left, min, max, hd - 1,
map);
findHorizontalDistance(node.right, min, max, hd + 1,
map);
}
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
tree.root.right.left.right = new Node(8);
tree.root.right.right.right = new Node(9);
System.out.println("vertical order traversal is :");
tree.verticalOrder(tree.root);
}
}
|
C#
using System;
using System.Collections.Generic;
public class Node {
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree {
public Node root;
public class Values {
public int max, min;
}
public void verticalOrder(Node node)
{
Values val = new Values();
SortedDictionary<int, List<int> > map
= new SortedDictionary<int, List<int> >();
findHorizontalDistance(node, val, val, 0, map);
foreach(List<int> list in map.Values)
{
Console.WriteLine(String.Join(" ", list));
}
}
public static void findHorizontalDistance(
Node node, Values min, Values max, int hd,
SortedDictionary<int, List<int> > map)
{
if (node == null)
return;
if (hd < min.min)
min.min = hd;
if (hd > max.max)
max.max = hd;
if (!map.TryGetValue(hd, out List<int> value)) {
value = new List<int>();
map.Add(hd, value);
}
value.Add(node.data);
findHorizontalDistance(node.left, min, max, hd - 1,
map);
findHorizontalDistance(node.right, min, max, hd + 1,
map);
}
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
tree.root.right.left.right = new Node(8);
tree.root.right.right.right = new Node(9);
Console.WriteLine("vertical order traversal is :");
tree.verticalOrder(tree.root);
}
}
|
Python3
class Node:
def __init__(self, item):
self.data = item
self.left = None
self.right = None
class BinaryTree:
def __init__(self):
self.root = None
class Values:
def __init__(self):
self.max = float('-inf')
self.min = float('inf')
def verticalOrder(self, node):
val = self.Values()
mp = {}
self.findHorizontalDistance(node, val, val, 0, mp)
for hd, lst in sorted(mp.items()):
for element in lst:
print(element, end=" ")
print()
def findHorizontalDistance(self, node, minVal, maxVal, hd, mp):
if node is None:
return
if hd < minVal.min:
minVal.min = hd
if hd > maxVal.max:
maxVal.max = hd
mp.setdefault(hd, []).append(node.data)
self.findHorizontalDistance(node.left, minVal, maxVal, hd - 1, mp)
self.findHorizontalDistance(node.right, minVal, maxVal, hd + 1, mp)
if __name__ == '__main__':
tree = BinaryTree()
tree.root = Node(1)
tree.root.left = Node(2)
tree.root.right = Node(3)
tree.root.left.left = Node(4)
tree.root.left.right = Node(5)
tree.root.right.left = Node(6)
tree.root.right.right = Node(7)
tree.root.right.left.right = Node(8)
tree.root.right.right.right = Node(9)
print("Vertical order traversal is:\n")
tree.verticalOrder(tree.root)
|
Javascript
class Node {
constructor(item) {
this.data = item;
this.left = null;
this.right = null;
}
}
class BinaryTree {
constructor() {
this.root = null;
}
verticalOrder(node) {
let val = new Values();
let mp = {};
this.findHorizontalDistance(node, val, val, 0, mp);
for (let hd of Object.keys(mp).sort((a, b) => a - b)) {
let lst = mp[hd];
for (let element of lst) {
process.stdout.write(element + " ");
}
process.stdout.write("\n");
}
}
findHorizontalDistance(node, minVal, maxVal, hd, mp) {
if (!node) {
return;
}
if (hd < minVal.min) {
minVal.min = hd;
}
if (hd > maxVal.max) {
maxVal.max = hd;
}
if (!mp[hd]) {
mp[hd] = [];
}
mp[hd].push(node.data);
this.findHorizontalDistance(node.left, minVal, maxVal, hd - 1, mp);
this.findHorizontalDistance(node.right, minVal, maxVal, hd + 1, mp);
}
}
class Values {
constructor() {
this.max = -Infinity;
this.min = Infinity;
}
}
let tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
tree.root.right.left.right = new Node(8);
tree.root.right.right.right = new Node(9);
process.stdout.write("Vertical order traversal is:\n");
tree.verticalOrder(tree.root);
|
Output
vertical order traversal is :
[4]
[2]
[1, 5, 6]
[3, 8]
[7]
[9]
Time Complexity: O(N Log N)
Auxiliary Space: O(N)
Vertical order traversal of the binary tree using the Unordered Map method:
Note: We have seen the ordered map above but, its complexity is O(N log N), and also it does not print the vertical nodes of the same horizontal distance in the correct order.
Here we implement this using an unordered map, as the unordered map is implemented using a hash table its complexity is O(n), better than using an ordered map which is implemented using a BST.
Follow the below steps to solve the problem:
- Create a queue of pair to store the node and its horizontal distance in the tree
- Create a map to store the value of nodes at each horizontal distance
- Now perform a BFS on the tree
- At each iteration store the nodes with a particular horizontal distance in the map
- Push the left and the right child of the tree with horizontal distance – 1 and horizontal distance + 1 into the queue
- Print the answer using map
Note: Here for printing all nodes of the same horizontal distance from the root we use mn and mx two variables that store the minimum and maximum horizontal distance from the root:
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int key;
Node *left, *right;
};
Node* newNode(int key)
{
Node* node = new Node;
node->key = key;
node->left = node->right = NULL;
return node;
}
void printVerticalOrder(Node* root)
{
if (!root)
return;
unordered_map<int, vector<int> > m;
int hd = 0;
queue<pair<Node*, int> > q;
q.push({ root, hd });
int mn = 0, mx = 0;
while (q.size() > 0) {
pair<Node*, int> temp = q.front();
q.pop();
hd = temp.second;
Node* node = temp.first;
m[hd].push_back(node->key);
if (node->left)
q.push({ node->left, hd - 1 });
if (node->right)
q.push({ node->right, hd + 1 });
if (mn > hd)
mn = hd;
else if (mx < hd)
mx = hd;
}
for (int i = mn; i <= mx; i++) {
vector<int> tmp = m[i];
for (int j = 0; j < tmp.size(); j++)
cout << tmp[j] << " ";
cout << endl;
}
}
int main()
{
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
root->right->left->right = newNode(8);
root->right->right->right = newNode(9);
cout << "Vertical order traversal is \n";
printVerticalOrder(root);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG {
static class Node {
int key;
Node left, right;
Node(int key)
{
this.key = key;
left = null;
right = null;
}
}
static class pair {
Node first;
int second;
pair(Node first, int second)
{
this.first = first;
this.second = second;
}
}
static void printVerticalOrder(Node root)
{
if (root == null)
return;
HashMap<Integer, ArrayList<Integer> > m
= new HashMap<>();
int hd = 0;
Queue<pair> q = new ArrayDeque<>();
q.add(new pair(root, hd));
int mn = 0, mx = 0;
while (q.size() > 0) {
pair temp = q.remove();
hd = temp.second;
Node node = temp.first;
if (!m.containsKey(hd))
m.put(hd, new ArrayList<>());
m.get(hd).add(node.key);
if (node.left != null)
q.add(new pair(node.left, hd - 1));
if (node.right != null)
q.add(new pair(node.right, hd + 1));
if (mn > hd)
mn = hd;
else if (mx < hd)
mx = hd;
}
for (int i = mn; i <= mx; i++) {
ArrayList<Integer> tmp = m.get(i);
for (int j = 0; j < tmp.size(); j++)
System.out.print(tmp.get(j) + " ");
System.out.println();
}
}
public static void main(String[] args)
{
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.right.left.right = new Node(8);
root.right.right.right = new Node(9);
System.out.println("Vertical order traversal is ");
printVerticalOrder(root);
}
}
|
C#
using System;
using System.Collections.Generic;
class GFG
{
class Node
{
public int key;
public Node left, right;
public Node (int key)
{
this.key = key;
left = null;
right = null;
}
}
class pair
{
public Node first;
public int second;
public pair (Node first, int second)
{
this.first = first;
this.second = second;
}
}
static void printVerticalOrder (Node root)
{
if (root == null)
return;
Dictionary < int, List < int >>m = new Dictionary < int, List < int >>();
int hd = 0;
Queue < pair > q = new Queue < pair > ();
q.Enqueue (new pair (root, hd));
int mn = 0, mx = 0;
while (q.Count > 0)
{
pair temp = q.Dequeue ();
hd = temp.second;
Node node = temp.first;
if (!m.ContainsKey (hd))
m.Add (hd, new List < int >());
m[hd].Add (node.key);
if (node.left != null)
q.Enqueue (new pair (node.left, hd - 1));
if (node.right != null)
q.Enqueue (new pair (node.right, hd + 1));
if (mn > hd)
mn = hd;
else if (mx < hd)
mx = hd;
}
for (int i = mn; i <= mx; i++)
{
List < int >tmp = m[i];
for (int j = 0; j < tmp.Count; j++)
Console.Write (tmp[j] + " ");
Console.WriteLine ();
}
}
static void Main ()
{
Node root = new Node (1);
root.left = new Node (2);
root.right = new Node (3);
root.left.left = new Node (4);
root.left.right = new Node (5);
root.right.left = new Node (6);
root.right.right = new Node (7);
root.right.left.right = new Node (8);
root.right.right.right = new Node (9);
Console.WriteLine ("Vertical order traversal is ");
printVerticalOrder (root);
}
}
|
Javascript
class Queue {
constructor() {
this.items = Array.from(Array(), () => new Array());
}
push(element) {
return this.items.push(element);
}
pop() {
if (this.items.length > 0) {
return this.items.shift();
}
}
front() {
return this.items[0];
}
empty() {
return this.items.length == 0;
}
size() {
return this.items.length;
}
}
class Node {
constructor(key) {
this.key = key;
this.left = null;
this.right = null;
}
}
function printVerticalOrder(root) {
if (!root) return;
let m = new Map();
let hd = 0;
let q = new Queue();
q.push([root, hd]);
let mn = 0,
mx = 0;
while (q.size() > 0) {
temp = q.front();
q.pop();
hd = temp[1];
node = temp[0];
if (m.get(hd) === undefined) {
m.set(hd, "" + node.key);
} else {
m.set(hd, m.get(hd) + " " + node.key);
}
if (node.left) q.push([node.left, hd - 1]);
if (node.right) q.push([node.right, hd + 1]);
if (mn > hd) mn = hd;
else if (mx < hd) mx = hd;
}
for (let i = mn; i <= mx; i++) {
tmp = m.get(i);
console.log(tmp);
}
}
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.right.left.right = new Node(8);
root.right.right.right = new Node(9);
console.log("Vertical order traversal is ");
printVerticalOrder(root);
|
Python3
class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
def newNode(key):
node = Node(key)
return node
def printVerticalOrder(root):
if not root:
return
m = {}
hd = 0
q = []
q.append((root, hd))
mn, mx = 0, 0
while q:
temp = q.pop(0)
hd = temp[1]
node = temp[0]
if hd in m:
m[hd].append(node.key)
else:
m[hd] = [node.key]
if node.left:
q.append((node.left, hd - 1))
if node.right:
q.append((node.right, hd + 1))
if mn > hd:
mn = hd
elif mx < hd:
mx = hd
for i in range(mn, mx+1):
if i in m:
tmp = m[i]
for j in range(len(tmp)):
print(tmp[j], end=' ')
print()
if __name__ == '__main__':
root = newNode(1)
root.left = newNode(2)
root.right = newNode(3)
root.left.left = newNode(4)
root.left.right = newNode(5)
root.right.left = newNode(6)
root.right.right = newNode(7)
root.right.left.right = newNode(8)
root.right.right.right = newNode(9)
print("Vertical order traversal is")
printVerticalOrder(root)
|
Output
Vertical order traversal is
4
2
1 5 6
3 8
7
9
Time Complexity: O(N)
Auxiliary Space: O(N)
Share your thoughts in the comments
Please Login to comment...