Phong model (Specular Reflection) in Computer Graphics
Last Updated :
07 Apr, 2021
Prerequisite – Basic Illumination Models
Phong model of reflection :
When we look at illuminated shiny surfaces, such as glittering surfaces, polished metal sheets, apple etc, we found a kind of bright spot at certain viewing point locations. This phenomenon is called specular reflection.
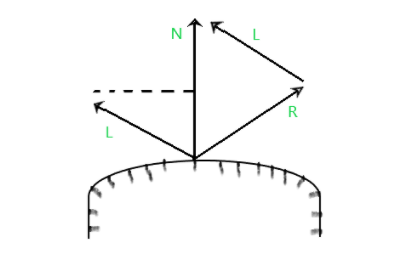
Look at the following figure :
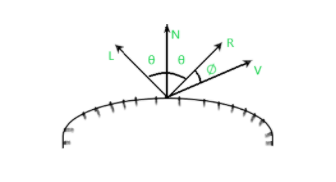
N = Normal vector
L = Point light source
V = Viewing direction
R = is representing the unit vector directed towards the ideal specular reflection
∅ = Viewing angle relative to the specular reflection direction R.
θ = Angle made by L & R with N.
For ideal reflector surfaces(perfect mirror), incident light is reflected only in the specular-reflection direction. So, in this case, we could be able to see reflected light when vectors V & R coincides(viewing angle(∅=0)).
A Shiny surface has a narrow specular reflection range, while a dull surface has a wider reflection range. An empirical model for calculating the specular reflection range, invented by the Phong Bui Tuong is also known as Phong specular reflection model. This model sets the intensity of specular reflection directly proportional to the cosns(∅). The range of angle ∅ can lie between 0 ≤ ∅ ≤ 1. Where ns is a specular reflection parameter whose value is determined by the type of surface to be displayed. The value of ns for brighter(shiny) surfaces could be 100 or more whereas for dull surfaces its value is 1 or less than 1. The intensity of specular reflection depends on the object(Material) properties of the surface & the angle of light incidence, as well as other factors such as the polarization and color of the light incident.
We can control the intensity variation of the light through, specular-reflection, using spectral-reflection function W(∅) for each surface. Where ∅ the value lies in the range of 0 ≤ ∅ ≤ 1. In general W(∅) tend to increase as the angle of incidence increases, at ∅=90* W(90*)=1, and in this case, all the light incidents on the surface of the material is reflected. So, using the spectral-reflection function W(∅) we can write the Phong specular reflection model as :

For many opaque material surfaces, specular reflections are nearly constant for all incident angles. So, in such case, we can replace W(∅) with a constant coefficient(Ks), and the value lies between 0 & 1, for each surface:
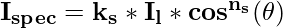
Since, V & R are unit vectors so, |V|=|R|=1 :
V * R = |V|*|R|*cos(θ) ,
V * R = cos(θ)
So, we can write just the previous equation as:
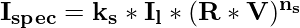
Here, R can be calculated by the projection of L onto the direction of the normal vector is obtained:
R + L = (2*N.L)*N
So, using the above equation specular-reflection vector is obtained,
R = (2*N.L)*N - L.
Combined ambient, diffuse and specular reflections in the Phong model can be represented as the following equation with multiple light sources:
So, for a single point light source, we can model the combined & specular reflections from a point on an illuminated surface as :
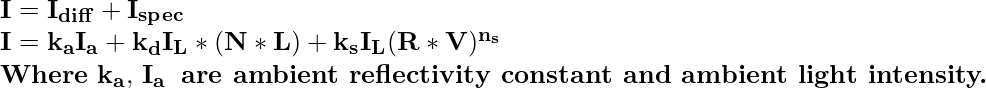
And, for n point light source, the equation will be:
![Rendered by QuickLaTeX.com \mathbf{I=k_aI_a+\Sigma_{i=1}^{n}[k_dI_L*(N*L)+k_sI_L(R*V)^{n_s}]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fc1cf5bc1ca847a0f5f1ceb9ff93c04c_l3.png)
Share your thoughts in the comments
Please Login to comment...