Optimal Strategy for a Game | Set 2

Problem statement: Consider a row of n coins of values v1 . . . vn, where n is even. We play a game against an opponent by alternating turns. In each turn, a player selects either the first or last coin from the row, removes it from the row permanently, and receives the value of the coin. Determine the maximum possible amount of money we can definitely win if we move first.
Note: The opponent is as clever as the user.

Let us understand the problem with a few examples:

1. 5, 3, 7, 10 : The user collects maximum value as 15(10 + 5)
2. 8, 15, 3, 7 : The user collects maximum value as 22(7 + 15)
Does choosing the best at each move give an optimal solution?
No. In the second example, this is how the game can finish:
1.
…….User chooses 8.
…….Opponent chooses 15.
…….User chooses 7.
…….Opponent chooses 3.
Total value collected by user is 15(8 + 7)
2.
…….User chooses 7.
…….Opponent chooses 8.
…….User chooses 15.
…….Opponent chooses 3.
Total value collected by user is 22(7 + 15)

So if the user follows the second game state, the maximum value can be collected although the first move is not the best.

We have discussed an approach that makes 4 recursive calls. In this post, a new approach is discussed that makes two recursive calls.
There are two choices:

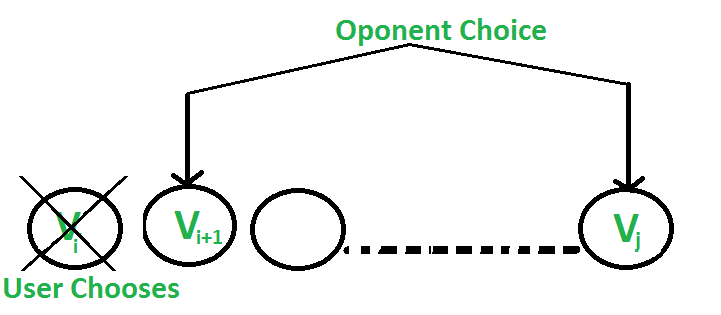
1. The user chooses the ith coin with value Vi: The opponent either chooses (i+1)th coin or jth coin. The opponent intends to choose the coin which leaves the user with minimum value.
i.e. The user can collect the value Vi + (Sum – Vi) – F(i+1, j, Sum – Vi) where Sum is sum of coins from index i to j. The expression can be simplified to Sum – F(i+1, j, Sum – Vi)

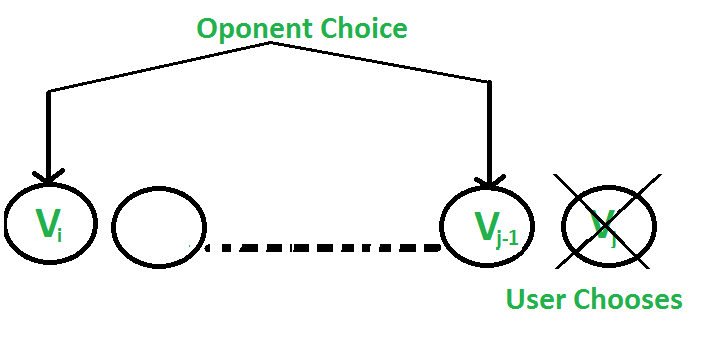
2. The user chooses the jth coin with value Vj: The opponent either chooses ith coin or (j-1)th coin. The opponent intends to choose the coin which leaves the user with minimum value.
i.e. The user can collect the value Vj + (Sum – Vj) – F(i, j-1, Sum – Vj) where Sum is sum of coins from index i to j. The expression can be simplified to Sum – F(i, j-1, Sum – Vj)

The following is the recursive solution that is based on the above two choices. We take a maximum of two choices.

F(i, j) represents the maximum value the user can collect from
i’th coin to j’th coin.
arr[] represents the list of coins
F(i, j) = Max(Sum – F(i+1, j, Sum-arr[i]),
Sum – F(i, j-1, Sum-arr[j]))
Base Case
F(i, j) = max(arr[i], arr[j]) If j == i+1

Simple Recursive Solution :

C++

// C++ program to find out maximum value from a
// given sequence of coins
#include <bits/stdc++.h>
using namespace std;
 
int oSRec(int arr[], int i, int j, int sum)
{
    if (j == i + 1)
        return max(arr[i], arr[j]);
 
    // For both of your choices, the opponent
    // gives you total sum minus maximum of
    // his value
    return max((sum - oSRec(arr, i + 1, j, sum - arr[i])),
               (sum - oSRec(arr, i, j - 1, sum - arr[j])));
}
 
// Returns optimal value possible that a player can
// collect from an array of coins of size n. Note
// than n must be even
int optimalStrategyOfGame(int* arr, int n)
{
    int sum = 0;
    sum = accumulate(arr, arr + n, sum);
    return oSRec(arr, 0, n - 1, sum);
}
 
// Driver program to test above function
int main()
{
    int arr1[] = { 8, 15, 3, 7 };
    int n = sizeof(arr1) / sizeof(arr1[0]);
    printf("%d\n", optimalStrategyOfGame(arr1, n));
 
    int arr2[] = { 2, 2, 2, 2 };
    n = sizeof(arr2) / sizeof(arr2[0]);
    printf("%d\n", optimalStrategyOfGame(arr2, n));
 
    int arr3[] = { 20, 30, 2, 2, 2, 10 };
    n = sizeof(arr3) / sizeof(arr3[0]);
    printf("%d\n", optimalStrategyOfGame(arr3, n));
 
    return 0;
}

Java

// Java program to find out maximum value from a
// given sequence of coins
import java.io.*;
 
class GFG {
 
    static int oSRec(int[] arr, int i, int j, int sum)
    {
        if (j == i + 1)
            return Math.max(arr[i], arr[j]);
 
        // For both of your choices, the opponent
        // gives you total sum minus maximum of
        // his value
        return Math.max(
            (sum - oSRec(arr, i + 1, j, sum - arr[i])),
            (sum - oSRec(arr, i, j - 1, sum - arr[j])));
    }
 
    // Returns optimal value possible that a player can
    // collect from an array of coins of size n. Note
    // than n must be even
    static int optimalStrategyOfGame(int[] arr, int n)
    {
        int sum = 0;
        for (int i = 0; i < n; i++) {
            sum += arr[i];
        }
 
        return oSRec(arr, 0, n - 1, sum);
    }
 
    // Driver code
    static public void main(String[] args)
    {
        int[] arr1 = { 8, 15, 3, 7 };
        int n = arr1.length;
        System.out.println(optimalStrategyOfGame(arr1, n));
 
        int[] arr2 = { 2, 2, 2, 2 };
        n = arr2.length;
        System.out.println(optimalStrategyOfGame(arr2, n));
 
        int[] arr3 = { 20, 30, 2, 2, 2, 10 };
        n = arr3.length;
        System.out.println(optimalStrategyOfGame(arr3, n));
    }
}
 
// This code is contributed by anuj_67..

Python3

# python3 program to find out maximum value from a
# given sequence of coins
 
 
def oSRec(arr, i, j, Sum):
 
    if (j == i + 1):
        return max(arr[i], arr[j])
 
    # For both of your choices, the opponent
    # gives you total Sum minus maximum of
    # his value
    return max((Sum - oSRec(arr, i + 1, j, Sum - arr[i])),
               (Sum - oSRec(arr, i, j - 1, Sum - arr[j])))
 
# Returns optimal value possible that a player can
# collect from an array of coins of size n. Note
# than n must be even
 
 
def optimalStrategyOfGame(arr, n):
 
    Sum = 0
    Sum = sum(arr)
    return oSRec(arr, 0, n - 1, Sum)
 
# Driver code
 
 
arr1 = [8, 15, 3, 7]
n = len(arr1)
print(optimalStrategyOfGame(arr1, n))
 
arr2 = [2, 2, 2, 2]
n = len(arr2)
print(optimalStrategyOfGame(arr2, n))
 
arr3 = [20, 30, 2, 2, 2, 10]
n = len(arr3)
print(optimalStrategyOfGame(arr3, n))
 
# This code is contributed by Mohit kumar 29

C#

// C# program to find out maximum value from a
// given sequence of coins
using System;
class GFG {
    static int oSRec(int[] arr, int i, int j, int sum)
    {
        if (j == i + 1)
            return Math.Max(arr[i], arr[j]);
 
        // For both of your choices, the opponent
        // gives you total sum minus maximum of
        // his value
        return Math.Max(
            (sum - oSRec(arr, i + 1, j, sum - arr[i])),
            (sum - oSRec(arr, i, j - 1, sum - arr[j])));
    }
 
    // Returns optimal value possible that a player can
    // collect from an array of coins of size n. Note
    // than n must be even
    static int optimalStrategyOfGame(int[] arr, int n)
    {
        int sum = 0;
        for (int i = 0; i < n; i++) {
            sum += arr[i];
        }
 
        return oSRec(arr, 0, n - 1, sum);
    }
 
    // Driver code
    static public void Main()
    {
        int[] arr1 = { 8, 15, 3, 7 };
        int n = arr1.Length;
        Console.WriteLine(optimalStrategyOfGame(arr1, n));
 
        int[] arr2 = { 2, 2, 2, 2 };
        n = arr2.Length;
        Console.WriteLine(optimalStrategyOfGame(arr2, n));
 
        int[] arr3 = { 20, 30, 2, 2, 2, 10 };
        n = arr3.Length;
        Console.WriteLine(optimalStrategyOfGame(arr3, n));
    }
}
 
// This code is contributed by AnkitRai01

Javascript

<script>
    // Javascript program to find out maximum value from a
    // given sequence of coins
     
    function oSRec(arr, i, j, sum)
    {
        if (j == i + 1)
            return Math.max(arr[i], arr[j]);
      
        // For both of your choices, the opponent
        // gives you total sum minus maximum of
        // his value
        return Math.max((sum - oSRec(arr, i + 1, j,
                                     sum - arr[i])),
                        (sum - oSRec(arr, i, j - 1,
                                     sum - arr[j])));
    }
      
    // Returns optimal value possible that a player can
    // collect from an array of coins of size n. Note
    // than n must be even
    function optimalStrategyOfGame(arr, n)
    {
        let sum = 0;
        for(let i = 0; i < n; i++)
        {
            sum += arr[i];
        }
  
        return oSRec(arr, 0, n - 1, sum);
    }
     
    let arr1 = [ 8, 15, 3, 7 ];
    let n = arr1.length;
    document.write(optimalStrategyOfGame(arr1, n) + "</br>");
 
    let arr2 = [ 2, 2, 2, 2 ];
    n = arr2.length;
    document.write(optimalStrategyOfGame(arr2, n) + "</br>");
 
    let arr3 = [ 20, 30, 2, 2, 2, 10 ];
    n = arr3.length;
    document.write(optimalStrategyOfGame(arr3, n) + "</br>");
 
</script>

Output

22
4
42

Time complexity : O(2^n)

Space Complexity : O(n)

Memoization Based Solution :

C++

// C++ program to find out maximum value from a
// given sequence of coins
#include <bits/stdc++.h>
using namespace std;
 
const int MAX = 100;
 
int memo[MAX][MAX];
 
int oSRec(int arr[], int i, int j, int sum)
{
    if (j == i + 1)
        return max(arr[i], arr[j]);
 
    if (memo[i][j] != -1)
        return memo[i][j];
 
    // For both of your choices, the opponent
    // gives you total sum minus maximum of
    // his value
    memo[i][j]
        = max((sum - oSRec(arr, i + 1, j, sum - arr[i])),
              (sum - oSRec(arr, i, j - 1, sum - arr[j])));
 
    return memo[i][j];
}
 
// Returns optimal value possible that a player can
// collect from an array of coins of size n. Note
// than n must be even
int optimalStrategyOfGame(int* arr, int n)
{
    // Compute sum of elements
    int sum = 0;
    sum = accumulate(arr, arr + n, sum);
 
    // Initialize memoization table
    memset(memo, -1, sizeof(memo));
 
    return oSRec(arr, 0, n - 1, sum);
}
 
// Driver program to test above function
int main()
{
    int arr1[] = { 8, 15, 3, 7 };
    int n = sizeof(arr1) / sizeof(arr1[0]);
    printf("%d\n", optimalStrategyOfGame(arr1, n));
 
    int arr2[] = { 2, 2, 2, 2 };
    n = sizeof(arr2) / sizeof(arr2[0]);
    printf("%d\n", optimalStrategyOfGame(arr2, n));
 
    int arr3[] = { 20, 30, 2, 2, 2, 10 };
    n = sizeof(arr3) / sizeof(arr3[0]);
    printf("%d\n", optimalStrategyOfGame(arr3, n));
 
    return 0;
}

Java

// Java program to find out maximum value from a
// given sequence of coins
import java.util.*;
class GFG {
 
    static int MAX = 100;
 
    static int[][] memo = new int[MAX][MAX];
 
    static int oSRec(int arr[], int i, int j, int sum)
    {
        if (j == i + 1)
            return Math.max(arr[i], arr[j]);
 
        if (memo[i][j] != -1)
            return memo[i][j];
 
        // For both of your choices, the opponent
        // gives you total sum minus maximum of
        // his value
        memo[i][j] = Math.max(
            (sum - oSRec(arr, i + 1, j, sum - arr[i])),
            (sum - oSRec(arr, i, j - 1, sum - arr[j])));
 
        return memo[i][j];
    }
 
    static int accumulate(int[] arr, int start, int end)
    {
        int sum = 0;
        for (int i = 0; i < arr.length; i++)
            sum += arr[i];
        return sum;
    }
 
    // Returns optimal value possible that a player can
    // collect from an array of coins of size n. Note
    // than n must be even
    static int optimalStrategyOfGame(int[] arr, int n)
    {
        // Compute sum of elements
        int sum = 0;
        sum = accumulate(arr, 0, n);
 
        // Initialize memoization table
        for (int j = 0; j < MAX; j++) {
            for (int k = 0; k < MAX; k++)
                memo[j][k] = -1;
        }
 
        return oSRec(arr, 0, n - 1, sum);
    }
 
    // Driver Code
    public static void main(String[] args)
    {
        int arr1[] = { 8, 15, 3, 7 };
        int n = arr1.length;
        System.out.printf("%d\n",
                          optimalStrategyOfGame(arr1, n));
 
        int arr2[] = { 2, 2, 2, 2 };
        n = arr2.length;
        System.out.printf("%d\n",
                          optimalStrategyOfGame(arr2, n));
 
        int arr3[] = { 20, 30, 2, 2, 2, 10 };
        n = arr3.length;
        System.out.printf("%d\n",
                          optimalStrategyOfGame(arr3, n));
    }
}
 
// This code is contributed by gauravrajput1

Python3

# Python3 program to find out maximum value
# from a given sequence of coins
MAX = 100
 
memo = [[0 for i in range(MAX)]
        for j in range(MAX)]
 
 
def oSRec(arr, i, j, Sum):
 
    if (j == i + 1):
        return max(arr[i], arr[j])
 
    if (memo[i][j] != -1):
        return memo[i][j]
 
    # For both of your choices, the opponent
    # gives you total sum minus maximum of
    # his value
    memo[i][j] = max((Sum - oSRec(arr, i + 1, j,
                                  Sum - arr[i])),
                     (Sum - oSRec(arr, i, j - 1,
                                  Sum - arr[j])))
 
    return memo[i][j]
 
# Returns optimal value possible that a
# player can collect from an array of
# coins of size n. Note than n must
# be even
 
 
def optimalStrategyOfGame(arr, n):
 
    # Compute sum of elements
    Sum = 0
    Sum = sum(arr)
 
    # Initialize memoization table
    for j in range(MAX):
        for k in range(MAX):
            memo[j][k] = -1
 
    return oSRec(arr, 0, n - 1, Sum)
 
 
# Driver Code
arr1 = [8, 15, 3, 7]
n = len(arr1)
print(optimalStrategyOfGame(arr1, n))
 
arr2 = [2, 2, 2, 2]
n = len(arr2)
print(optimalStrategyOfGame(arr2, n))
 
arr3 = [20, 30, 2, 2, 2, 10]
n = len(arr3)
print(optimalStrategyOfGame(arr3, n))
 
# This code is contributed by divyesh072019

C#

// C# program to find out maximum value from a
// given sequence of coins
using System;
class GFG {
 
    static int MAX = 100;
 
    static int[, ] memo = new int[MAX, MAX];
 
    static int oSRec(int[] arr, int i, int j, int sum)
    {
        if (j == i + 1)
            return Math.Max(arr[i], arr[j]);
 
        if (memo[i, j] != -1)
            return memo[i, j];
 
        // For both of your choices, the opponent
        // gives you total sum minus maximum of
        // his value
        memo[i, j] = Math.Max(
            (sum - oSRec(arr, i + 1, j, sum - arr[i])),
            (sum - oSRec(arr, i, j - 1, sum - arr[j])));
 
        return memo[i, j];
    }
 
    static int accumulate(int[] arr, int start, int end)
    {
        int sum = 0;
        for (int i = 0; i < arr.Length; i++)
            sum += arr[i];
        return sum;
    }
 
    // Returns optimal value possible that a player can
    // collect from an array of coins of size n. Note
    // than n must be even
    static int optimalStrategyOfGame(int[] arr, int n)
    {
        // Compute sum of elements
        int sum = 0;
        sum = accumulate(arr, 0, n);
 
        // Initialize memoization table
        for (int j = 0; j < MAX; j++) {
            for (int k = 0; k < MAX; k++)
                memo[j, k] = -1;
        }
 
        return oSRec(arr, 0, n - 1, sum);
    }
 
    // Driver Code
    public static void Main(String[] args)
    {
        int[] arr1 = { 8, 15, 3, 7 };
        int n = arr1.Length;
        Console.Write("{0}\n",
                      optimalStrategyOfGame(arr1, n));
 
        int[] arr2 = { 2, 2, 2, 2 };
        n = arr2.Length;
        Console.Write("{0}\n",
                      optimalStrategyOfGame(arr2, n));
 
        int[] arr3 = { 20, 30, 2, 2, 2, 10 };
        n = arr3.Length;
        Console.Write("{0}\n",
                      optimalStrategyOfGame(arr3, n));
    }
}
 
// This code is contributed by Rohit_ranjan

Javascript

<script>
 
// Javascript program to find out maximum
// value from a given sequence of coins
let MAX = 100;
let memo = new Array(MAX);
for(let i = 0; i < MAX; i++)
{
    memo[i] = new Array(MAX);
    for(let j = 0; j < MAX; j++)
    {
        memo[i][j] = 0;
    }
}
 
function oSRec(arr, i, j, sum)
{
    if (j == i + 1)
        return Math.max(arr[i], arr[j]);
  
    if (memo[i][j] != -1)
        return memo[i][j];
  
    // For both of your choices, the opponent
    // gives you total sum minus maximum of
    // his value
    memo[i][j] = Math.max((sum - oSRec(arr, i + 1, j,
                                       sum - arr[i])),
                          (sum - oSRec(arr, i, j - 1,
                                       sum - arr[j])));
  
    return memo[i][j];
}
 
function accumulate(arr, start, end)
{
     let sum = 0;
    for(let i = 0; i < arr.length; i++)
        sum += arr[i];
         
    return sum;
}
 
// Returns optimal value possible that a player can
// collect from an array of coins of size n. Note
// than n must be even
function optimalStrategyOfGame(arr, n)
{
     
    // Compute sum of elements
    let sum = 0;
    sum = accumulate(arr, 0, n);
  
    // Initialize memoization table
    for(let j = 0; j < MAX; j++)
    {
        for(let k = 0; k < MAX; k++)
            memo[j][k] = -1;
    }
    return oSRec(arr, 0, n - 1, sum);
}
 
// Driver Code
let arr1 = [ 8, 15, 3, 7 ];
let n = arr1.length;
document.write(
    optimalStrategyOfGame(arr1, n) + "<br>");
                
let arr2 = [ 2, 2, 2, 2 ];
n = arr2.length;
document.write(
    optimalStrategyOfGame(arr2, n) + "<br>");
                
let arr3 = [ 20, 30, 2, 2, 2, 10 ];
n = arr3.length;
document.write(
    optimalStrategyOfGame(arr3, n) + "<br>");
 
// This code is contributed by patel2127
 
</script>

Output

22
4
42

Time Complexity : O(n^2)

Space Complexity : O(n^2)

Another Approach: Another idea to easily solve the problem is :

If we denote the coins collected by us as a positive score of an equivalent amount, whereas the coins removed by our opponent with a negative score of an equivalent amount, then the problem transforms to maximizing our score if we go first.
Let us denote dp[i][j] as the maximum score a player can get in the subarray [i . . . j], then
dp[i][j] = max(arr[i]-dp[i+1][j], arr[j]-dp[i][j-1])

This dynamic programming relation can be justified as mentioned below:

This relation holds because
If we pick the leftmost element, then we would get a score equivalent to
arr[i] – the maximum amount our opponent can get from the subarray [(i+1) … j].
Similarly picking the rightmost element will get us a score equivalent to
arr[j] – the maximum amount of score our opponent gets from the subarray [i … (j-1)].
This can be solved using the simple Dynamic Programming relation given above. The final answer would be contained in dp[0][n-1].
However, we still need to account for the impact of introducing the negative score.
Suppose dp[0][n-1] equals VAL, the sum of all the scores equals SUM, and the total score of our opponent equals OPP,
Then according to the original problem we are supposed to calculate abs(OPP) + VAL since our opponent does not have any negative impact on our final answer according to the original problem statement.
This value can be easily calculated as,
VAL + 2*abs(OPP) = SUM
(OPP removed by our opponent implies that we had gained OPP amount as well, hence the 2*abs(OPP))
=> VAL + abs(OPP) = (SUM + VAL)/2

The implementation of the above approach is given below.

C++

#include <bits/stdc++.h>
using namespace std;
 
// Function to find the maximum possible
// amount of money we can win.
long long maximumAmount(int arr[], int n)
{
    long long sum = 0;
    vector<vector<long long> > dp(n,vector<long long>(n, 0));
    for (int i = (n - 1); i >= 0; i--) {
         
        // Calculating the sum of all the elements
        sum += arr[i];
        for (int j = i; j < n; j++) {
            if (i == j) {
                 
                // If there is only one element then we
                // can only get arr[i] score
                dp[i][j] = arr[i];
            }
            else {
                // Calculating the dp states
                // using the relation
                dp[i][j] = max(arr[i] - dp[i + 1][j],
                               arr[j] - dp[i][j - 1]);
            }
        }
    }
    // Equating and returning the final answer
    // as per the relation
    return (sum + dp[0][n - 1]) / 2;
}
 
// Driver Code
int main()
{
    int arr1[] = { 8, 15, 3, 7 };
    int n = sizeof(arr1) / sizeof(arr1[0]);
    printf("%lld\n", maximumAmount(arr1, n));
 
    return 0;
}
// This code is contributed by Ojassvi Kumar

Java

/*package whatever //do not write package name here */
import java.util.*;
 
class GFG {
   
  // Function to find the maximum possible
// amount of money we can win.
static long maximumAmount(int arr[], int n)
{
    long sum = 0;
    long dp[][] = new long[n][n];
    for (int i = (n - 1); i >= 0; i--) {
         
        // Calculating the sum of all the elements
        sum += arr[i];
        for (int j = i; j < n; j++) {
            if (i == j) {
                 
                // If there is only one element then we
                // can only get arr[i] score
                dp[i][j] = arr[i];
            }
            else {
                // Calculating the dp states
                // using the relation
                dp[i][j] = Math.max(arr[i] - dp[i + 1][j],arr[j] - dp[i][j - 1]);
            }
        }
    }
   
    // Equating and returning the final answer
    // as per the relation
    return (sum + dp[0][n - 1]) / 2;
}
    public static void main (String[] args) {
         int arr1[] = { 8, 15, 3, 7 };
    int n = arr1.length;
    System.out.println(maximumAmount(arr1, n));
 
    }
}
 
// This code is contributed by utkarshshirode02

Python3

# Function to find the maximum possible
# amount of money we can win.
 
import math
 
def maximumAmount(arr, n):
    sum = 0;
    dp=[[0]*n for _ in range(n)];
    for i in range(n-1, -1, -1):
         
        # Calculating the sum of all the elements
        sum += arr[i];
        for j in range(i,n):
            if (i == j):
                 
                # If there is only one element then we
                # can only get arr[i] score
                dp[i][j] = arr[i];
     
            else :
                # Calculating the dp states
                # using the relation
                dp[i][j] = max(arr[i] - dp[i + 1][j],
                               arr[j] - dp[i][j - 1]);
             
    # Equating and returning the final answer
    # as per the relation
    return math.floor((sum + dp[0][n - 1]) / 2);
 
# Driver Code
arr1 = [ 8, 15, 3, 7 ];
n = len(arr1);
print(maximumAmount(arr1, n));
 
# This code is contributed by ratiagarwal.

C#

using System;
 
public class GFG {
 
// Function to find the maximum possible
// amount of money we can win.
static long maximumAmount(int[] arr, int n)
{
    long sum = 0;
    long[,] dp = new long[n, n];
    for (int i = (n - 1); i >= 0; i--)
    {
         
        // Calculating the sum of all the elements
        sum += arr[i];
        for (int j = i; j < n; j++)
        {
            if (i == j)
            {
                 
                // If there is only one element then we
                // can only get arr[i] score
                dp[i, j] = arr[i];
            }
            else
            {
                // Calculating the dp states
                // using the relation
                dp[i, j] = Math.Max(arr[i] - dp[i + 1, j],
                                            arr[j] - dp[i, j - 1]);
            }
        }
    }
   
    // Equating and returning the final answer
    // as per the relation
    return (sum + dp[0, n - 1]) / 2;
}
 
// Driver code
public static void Main()
{
    int[] arr1 = { 8, 15, 3, 7 };
    int n = arr1.Length;
    Console.WriteLine(maximumAmount(arr1, n));
}
}
// This code is contributed by SRJ

Javascript

// Function to find the maximum possible
// amount of money we can win.
function maximumAmount(arr, n)
{
    let sum = 0;
    let dp= new Array(n);
    for(let i = 0; i < n; i++)
        dp[i] = new Array(n).fill(0);
    for (let i = (n - 1); i >= 0; i--) {
         
        // Calculating the sum of all the elements
        sum += arr[i];
        for (let j = i; j < n; j++) {
            if (i == j) {
                 
                // If there is only one element then we
                // can only get arr[i] score
                dp[i][j] = arr[i];
            }
            else
            {
             
                // Calculating the dp states
                // using the relation
                dp[i][j] = Math.max(arr[i] - dp[i + 1][j],
                               arr[j] - dp[i][j - 1]);
            }
        }
    }
     
    // Equating and returning the final answer
    // as per the relation
    return (sum + dp[0][n - 1]) / 2;
}
 
// Driver Code
let arr1 = [ 8, 15, 3, 7 ];
let n = arr1.length;
console.log(maximumAmount(arr1, n));
 
// This code is contributed by poojaagarwal2.

Output

Time Complexity : O(n^2)

Space Complexity : O(n^2),

Efficient approach : Space optimization

In previous approach the current value dp[i][j] is only depend upon the current and previous row values of DP. So to optimize the space complexity we use a single 1D array to store the computations.

Implementation steps:

Create a 1D vector dp of size n.
Set a base case by initializing the values of DP .
Now iterate over subproblems by the help of nested loop and get the current value from previous computations.
At last return final answer (sum + dp[n – 1]) / 2.

Implementation:

C++

#include <bits/stdc++.h>
using namespace std;
 
// Function to find the maximum possible
// amount of money we can win.
long long maximumAmount(int arr[], int n)
{
    long long sum = 0;
    vector<long long> dp(n, 0);
    for (int i = (n - 1); i >= 0; i--) {
 
        // Calculating the sum of all the elements
        sum += arr[i];
        for (int j = i; j < n; j++) {
            if (i == j) {
 
                // If there is only one element then we
                // can only get arr[i] score
                dp[j] = arr[j];
            }
            else {
                // Calculating the dp states
                // using the relation
                dp[j] = max(arr[i] - dp[j],
                            arr[j] - dp[j - 1]);
            }
        }
    }
    // Equating and returning the final answer
    // as per the relation
    return (sum + dp[n - 1]) / 2;
}
 
// Driver Code
int main()
{
    int arr1[] = { 8, 15, 3, 7 };
    int n = sizeof(arr1) / sizeof(arr1[0]);
    printf("%lld\n", maximumAmount(arr1, n));
 
    return 0;
}

Java

import java.util.*;
 
public class Main {
    // Function to find the maximum possible
    // amount of money we can win.
    public static long maximumAmount(int[] arr, int n)
    {
        long sum = 0;
        long[] dp = new long[n];
        Arrays.fill(dp, 0);
        for (int i = (n - 1); i >= 0; i--) {
 
            // Calculating the sum of all the elements
            sum += arr[i];
            for (int j = i; j < n; j++) {
                if (i == j) {
 
                    // If there is only one element then we
                    // can only get arr[i] score
                    dp[j] = arr[j];
                }
                else {
                    // Calculating the dp states
                    // using the relation
                    dp[j] = Math.max(arr[i] - dp[j],
                                     arr[j] - dp[j - 1]);
                }
            }
        }
        // Equating and returning the final answer
        // as per the relation
        return (sum + dp[n - 1]) / 2;
    }
 
    // Driver Code
    public static void main(String[] args)
    {
        int[] arr1 = { 8, 15, 3, 7 };
        int n = arr1.length;
        System.out.println(maximumAmount(arr1, n));
    }
}

Python3

def maximumAmount(arr, n):
    sum = 0
    dp = [0] * n
    for i in range(n - 1, -1, -1):
       
        # Calculating the sum of all the elements
        sum += arr[i]
        for j in range(i, n):
            if i == j:
               
                # If there is only one element then we
                # can only get arr[i] score
                dp[j] = arr[j]
            else:
               
                # Calculating the dp states
                # using the relation
                dp[j] = max(arr[i] - dp[j], arr[j] - dp[j - 1])
                 
    # Equating and returning the final answer
    # as per the relation
    return (sum + dp[n - 1]) // 2
 
 
arr1 = [8, 15, 3, 7]
n = len(arr1)
print(maximumAmount(arr1, n))

C#

using System;
 
class GFG
{
 
  // Function to find the maximum possible
  // amount of money we can win.
  static long maximumAmount(int[] arr, int n)
  {
    long sum = 0;
    long[] dp = new long[n];
    for (int i = (n - 1); i >= 0; i--) {
 
      // Calculating the sum of all the elements
      sum += arr[i];
      for (int j = i; j < n; j++) {
        if (i == j) {
 
          // If there is only one element then we
          // can only get arr[i] score
          dp[j] = arr[j];
        }
        else {
          // Calculating the dp states
          // using the relation
          dp[j] = Math.Max(arr[i] - dp[j],
                           arr[j] - dp[j - 1]);
        }
      }
    }
    // Equating and returning the final answer
    // as per the relation
    return (sum + dp[n - 1]) / 2;
  }
 
  // Driver Code
  static void Main()
  {
    int[] arr1 = { 8, 15, 3, 7 };
    int n = arr1.Length;
    Console.WriteLine(maximumAmount(arr1, n));
  }
}

Javascript

// Function to find the maximum possible
// amount of money we can win.
function maximumAmount(arr, n)
{
    let sum = 0;
    let dp = new Array(n).fill(0);
    for (let i = (n - 1); i >= 0; i--) {
 
        // Calculating the sum of all the elements
        sum += arr[i];
        for (let j = i; j < n; j++) {
            if (i == j) {
 
                // If there is only one element then we
                // can only get arr[i] score
                dp[j] = arr[j];
            }
            else {
                // Calculating the dp states
                // using the relation
                dp[j] = Math.max(arr[i] - dp[j],
                            arr[j] - dp[j - 1]);
            }
        }
    }
    // Equating and returning the final answer
    // as per the relation
    return Math.floor(sum + dp[n - 1]) / 2;
}
 
// Driver Code
let arr1 = [ 8, 15, 3, 7 ];
let n = arr1.length;
console.log(maximumAmount(arr1, n));