Optimal Strategy for a Game | Set 2
Last Updated :
31 Aug, 2023
Problem statement: Consider a row of n coins of values v1 . . . vn, where n is even. We play a game against an opponent by alternating turns. In each turn, a player selects either the first or last coin from the row, removes it from the row permanently, and receives the value of the coin. Determine the maximum possible amount of money we can definitely win if we move first.
Note: The opponent is as clever as the user.
Let us understand the problem with a few examples:
1. 5, 3, 7, 10 : The user collects maximum value as 15(10 + 5)
2. 8, 15, 3, 7 : The user collects maximum value as 22(7 + 15)
Does choosing the best at each move give an optimal solution?
No. In the second example, this is how the game can finish:
1.
…….User chooses 8.
…….Opponent chooses 15.
…….User chooses 7.
…….Opponent chooses 3.
Total value collected by user is 15(8 + 7)
2.
…….User chooses 7.
…….Opponent chooses 8.
…….User chooses 15.
…….Opponent chooses 3.
Total value collected by user is 22(7 + 15)
So if the user follows the second game state, the maximum value can be collected although the first move is not the best.
We have discussed an approach that makes 4 recursive calls. In this post, a new approach is discussed that makes two recursive calls.
There are two choices:
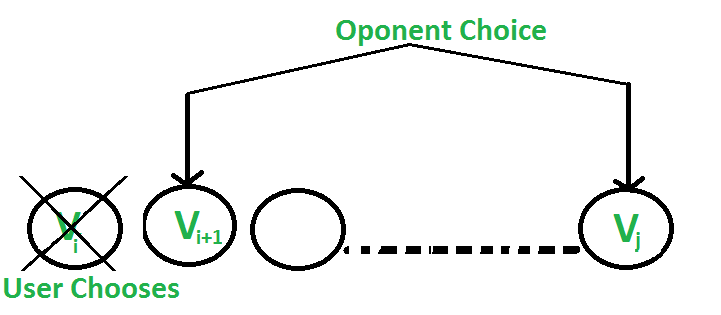
1. The user chooses the ith coin with value Vi: The opponent either chooses (i+1)th coin or jth coin. The opponent intends to choose the coin which leaves the user with minimum value.
i.e. The user can collect the value Vi + (Sum – Vi) – F(i+1, j, Sum – Vi) where Sum is sum of coins from index i to j. The expression can be simplified to Sum – F(i+1, j, Sum – Vi)
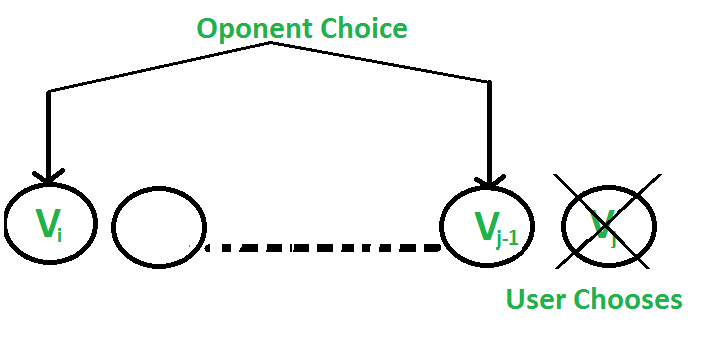
2. The user chooses the jth coin with value Vj: The opponent either chooses ith coin or (j-1)th coin. The opponent intends to choose the coin which leaves the user with minimum value.
i.e. The user can collect the value Vj + (Sum – Vj) – F(i, j-1, Sum – Vj) where Sum is sum of coins from index i to j. The expression can be simplified to Sum – F(i, j-1, Sum – Vj)
The following is the recursive solution that is based on the above two choices. We take a maximum of two choices.
F(i, j) represents the maximum value the user can collect from
i’th coin to j’th coin.
arr[] represents the list of coins
F(i, j) = Max(Sum – F(i+1, j, Sum-arr[i]),
Sum – F(i, j-1, Sum-arr[j]))
Base Case
F(i, j) = max(arr[i], arr[j]) If j == i+1
Simple Recursive Solution :
C++
#include <bits/stdc++.h>
using namespace std;
int oSRec(int arr[], int i, int j, int sum)
{
if (j == i + 1)
return max(arr[i], arr[j]);
return max((sum - oSRec(arr, i + 1, j, sum - arr[i])),
(sum - oSRec(arr, i, j - 1, sum - arr[j])));
}
int optimalStrategyOfGame(int* arr, int n)
{
int sum = 0;
sum = accumulate(arr, arr + n, sum);
return oSRec(arr, 0, n - 1, sum);
}
int main()
{
int arr1[] = { 8, 15, 3, 7 };
int n = sizeof(arr1) / sizeof(arr1[0]);
printf("%d\n", optimalStrategyOfGame(arr1, n));
int arr2[] = { 2, 2, 2, 2 };
n = sizeof(arr2) / sizeof(arr2[0]);
printf("%d\n", optimalStrategyOfGame(arr2, n));
int arr3[] = { 20, 30, 2, 2, 2, 10 };
n = sizeof(arr3) / sizeof(arr3[0]);
printf("%d\n", optimalStrategyOfGame(arr3, n));
return 0;
}
|
Java
import java.io.*;
class GFG {
static int oSRec(int[] arr, int i, int j, int sum)
{
if (j == i + 1)
return Math.max(arr[i], arr[j]);
return Math.max(
(sum - oSRec(arr, i + 1, j, sum - arr[i])),
(sum - oSRec(arr, i, j - 1, sum - arr[j])));
}
static int optimalStrategyOfGame(int[] arr, int n)
{
int sum = 0;
for (int i = 0; i < n; i++) {
sum += arr[i];
}
return oSRec(arr, 0, n - 1, sum);
}
static public void main(String[] args)
{
int[] arr1 = { 8, 15, 3, 7 };
int n = arr1.length;
System.out.println(optimalStrategyOfGame(arr1, n));
int[] arr2 = { 2, 2, 2, 2 };
n = arr2.length;
System.out.println(optimalStrategyOfGame(arr2, n));
int[] arr3 = { 20, 30, 2, 2, 2, 10 };
n = arr3.length;
System.out.println(optimalStrategyOfGame(arr3, n));
}
}
|
Python3
def oSRec(arr, i, j, Sum):
if (j == i + 1):
return max(arr[i], arr[j])
return max((Sum - oSRec(arr, i + 1, j, Sum - arr[i])),
(Sum - oSRec(arr, i, j - 1, Sum - arr[j])))
def optimalStrategyOfGame(arr, n):
Sum = 0
Sum = sum(arr)
return oSRec(arr, 0, n - 1, Sum)
arr1 = [8, 15, 3, 7]
n = len(arr1)
print(optimalStrategyOfGame(arr1, n))
arr2 = [2, 2, 2, 2]
n = len(arr2)
print(optimalStrategyOfGame(arr2, n))
arr3 = [20, 30, 2, 2, 2, 10]
n = len(arr3)
print(optimalStrategyOfGame(arr3, n))
|
C#
using System;
class GFG {
static int oSRec(int[] arr, int i, int j, int sum)
{
if (j == i + 1)
return Math.Max(arr[i], arr[j]);
return Math.Max(
(sum - oSRec(arr, i + 1, j, sum - arr[i])),
(sum - oSRec(arr, i, j - 1, sum - arr[j])));
}
static int optimalStrategyOfGame(int[] arr, int n)
{
int sum = 0;
for (int i = 0; i < n; i++) {
sum += arr[i];
}
return oSRec(arr, 0, n - 1, sum);
}
static public void Main()
{
int[] arr1 = { 8, 15, 3, 7 };
int n = arr1.Length;
Console.WriteLine(optimalStrategyOfGame(arr1, n));
int[] arr2 = { 2, 2, 2, 2 };
n = arr2.Length;
Console.WriteLine(optimalStrategyOfGame(arr2, n));
int[] arr3 = { 20, 30, 2, 2, 2, 10 };
n = arr3.Length;
Console.WriteLine(optimalStrategyOfGame(arr3, n));
}
}
|
Javascript
<script>
function oSRec(arr, i, j, sum)
{
if (j == i + 1)
return Math.max(arr[i], arr[j]);
return Math.max((sum - oSRec(arr, i + 1, j,
sum - arr[i])),
(sum - oSRec(arr, i, j - 1,
sum - arr[j])));
}
function optimalStrategyOfGame(arr, n)
{
let sum = 0;
for(let i = 0; i < n; i++)
{
sum += arr[i];
}
return oSRec(arr, 0, n - 1, sum);
}
let arr1 = [ 8, 15, 3, 7 ];
let n = arr1.length;
document.write(optimalStrategyOfGame(arr1, n) + "</br>");
let arr2 = [ 2, 2, 2, 2 ];
n = arr2.length;
document.write(optimalStrategyOfGame(arr2, n) + "</br>");
let arr3 = [ 20, 30, 2, 2, 2, 10 ];
n = arr3.length;
document.write(optimalStrategyOfGame(arr3, n) + "</br>");
</script>
|
Time complexity : O(2^n)
Space Complexity : O(n)
Memoization Based Solution :
C++
#include <bits/stdc++.h>
using namespace std;
const int MAX = 100;
int memo[MAX][MAX];
int oSRec(int arr[], int i, int j, int sum)
{
if (j == i + 1)
return max(arr[i], arr[j]);
if (memo[i][j] != -1)
return memo[i][j];
memo[i][j]
= max((sum - oSRec(arr, i + 1, j, sum - arr[i])),
(sum - oSRec(arr, i, j - 1, sum - arr[j])));
return memo[i][j];
}
int optimalStrategyOfGame(int* arr, int n)
{
int sum = 0;
sum = accumulate(arr, arr + n, sum);
memset(memo, -1, sizeof(memo));
return oSRec(arr, 0, n - 1, sum);
}
int main()
{
int arr1[] = { 8, 15, 3, 7 };
int n = sizeof(arr1) / sizeof(arr1[0]);
printf("%d\n", optimalStrategyOfGame(arr1, n));
int arr2[] = { 2, 2, 2, 2 };
n = sizeof(arr2) / sizeof(arr2[0]);
printf("%d\n", optimalStrategyOfGame(arr2, n));
int arr3[] = { 20, 30, 2, 2, 2, 10 };
n = sizeof(arr3) / sizeof(arr3[0]);
printf("%d\n", optimalStrategyOfGame(arr3, n));
return 0;
}
|
Java
import java.util.*;
class GFG {
static int MAX = 100;
static int[][] memo = new int[MAX][MAX];
static int oSRec(int arr[], int i, int j, int sum)
{
if (j == i + 1)
return Math.max(arr[i], arr[j]);
if (memo[i][j] != -1)
return memo[i][j];
memo[i][j] = Math.max(
(sum - oSRec(arr, i + 1, j, sum - arr[i])),
(sum - oSRec(arr, i, j - 1, sum - arr[j])));
return memo[i][j];
}
static int accumulate(int[] arr, int start, int end)
{
int sum = 0;
for (int i = 0; i < arr.length; i++)
sum += arr[i];
return sum;
}
static int optimalStrategyOfGame(int[] arr, int n)
{
int sum = 0;
sum = accumulate(arr, 0, n);
for (int j = 0; j < MAX; j++) {
for (int k = 0; k < MAX; k++)
memo[j][k] = -1;
}
return oSRec(arr, 0, n - 1, sum);
}
public static void main(String[] args)
{
int arr1[] = { 8, 15, 3, 7 };
int n = arr1.length;
System.out.printf("%d\n",
optimalStrategyOfGame(arr1, n));
int arr2[] = { 2, 2, 2, 2 };
n = arr2.length;
System.out.printf("%d\n",
optimalStrategyOfGame(arr2, n));
int arr3[] = { 20, 30, 2, 2, 2, 10 };
n = arr3.length;
System.out.printf("%d\n",
optimalStrategyOfGame(arr3, n));
}
}
|
Python3
MAX = 100
memo = [[0 for i in range(MAX)]
for j in range(MAX)]
def oSRec(arr, i, j, Sum):
if (j == i + 1):
return max(arr[i], arr[j])
if (memo[i][j] != -1):
return memo[i][j]
memo[i][j] = max((Sum - oSRec(arr, i + 1, j,
Sum - arr[i])),
(Sum - oSRec(arr, i, j - 1,
Sum - arr[j])))
return memo[i][j]
def optimalStrategyOfGame(arr, n):
Sum = 0
Sum = sum(arr)
for j in range(MAX):
for k in range(MAX):
memo[j][k] = -1
return oSRec(arr, 0, n - 1, Sum)
arr1 = [8, 15, 3, 7]
n = len(arr1)
print(optimalStrategyOfGame(arr1, n))
arr2 = [2, 2, 2, 2]
n = len(arr2)
print(optimalStrategyOfGame(arr2, n))
arr3 = [20, 30, 2, 2, 2, 10]
n = len(arr3)
print(optimalStrategyOfGame(arr3, n))
|
C#
using System;
class GFG {
static int MAX = 100;
static int[, ] memo = new int[MAX, MAX];
static int oSRec(int[] arr, int i, int j, int sum)
{
if (j == i + 1)
return Math.Max(arr[i], arr[j]);
if (memo[i, j] != -1)
return memo[i, j];
memo[i, j] = Math.Max(
(sum - oSRec(arr, i + 1, j, sum - arr[i])),
(sum - oSRec(arr, i, j - 1, sum - arr[j])));
return memo[i, j];
}
static int accumulate(int[] arr, int start, int end)
{
int sum = 0;
for (int i = 0; i < arr.Length; i++)
sum += arr[i];
return sum;
}
static int optimalStrategyOfGame(int[] arr, int n)
{
int sum = 0;
sum = accumulate(arr, 0, n);
for (int j = 0; j < MAX; j++) {
for (int k = 0; k < MAX; k++)
memo[j, k] = -1;
}
return oSRec(arr, 0, n - 1, sum);
}
public static void Main(String[] args)
{
int[] arr1 = { 8, 15, 3, 7 };
int n = arr1.Length;
Console.Write("{0}\n",
optimalStrategyOfGame(arr1, n));
int[] arr2 = { 2, 2, 2, 2 };
n = arr2.Length;
Console.Write("{0}\n",
optimalStrategyOfGame(arr2, n));
int[] arr3 = { 20, 30, 2, 2, 2, 10 };
n = arr3.Length;
Console.Write("{0}\n",
optimalStrategyOfGame(arr3, n));
}
}
|
Javascript
<script>
let MAX = 100;
let memo = new Array(MAX);
for(let i = 0; i < MAX; i++)
{
memo[i] = new Array(MAX);
for(let j = 0; j < MAX; j++)
{
memo[i][j] = 0;
}
}
function oSRec(arr, i, j, sum)
{
if (j == i + 1)
return Math.max(arr[i], arr[j]);
if (memo[i][j] != -1)
return memo[i][j];
memo[i][j] = Math.max((sum - oSRec(arr, i + 1, j,
sum - arr[i])),
(sum - oSRec(arr, i, j - 1,
sum - arr[j])));
return memo[i][j];
}
function accumulate(arr, start, end)
{
let sum = 0;
for(let i = 0; i < arr.length; i++)
sum += arr[i];
return sum;
}
function optimalStrategyOfGame(arr, n)
{
let sum = 0;
sum = accumulate(arr, 0, n);
for(let j = 0; j < MAX; j++)
{
for(let k = 0; k < MAX; k++)
memo[j][k] = -1;
}
return oSRec(arr, 0, n - 1, sum);
}
let arr1 = [ 8, 15, 3, 7 ];
let n = arr1.length;
document.write(
optimalStrategyOfGame(arr1, n) + "<br>");
let arr2 = [ 2, 2, 2, 2 ];
n = arr2.length;
document.write(
optimalStrategyOfGame(arr2, n) + "<br>");
let arr3 = [ 20, 30, 2, 2, 2, 10 ];
n = arr3.length;
document.write(
optimalStrategyOfGame(arr3, n) + "<br>");
</script>
|
Time Complexity : O(n^2)
Space Complexity : O(n^2)
Another Approach: Another idea to easily solve the problem is :
If we denote the coins collected by us as a positive score of an equivalent amount, whereas the coins removed by our opponent with a negative score of an equivalent amount, then the problem transforms to maximizing our score if we go first.
Let us denote dp[i][j] as the maximum score a player can get in the subarray [i . . . j], then
dp[i][j] = max(arr[i]-dp[i+1][j], arr[j]-dp[i][j-1])
This dynamic programming relation can be justified as mentioned below:
This relation holds because
- If we pick the leftmost element, then we would get a score equivalent to
arr[i] – the maximum amount our opponent can get from the subarray [(i+1) … j].
- Similarly picking the rightmost element will get us a score equivalent to
arr[j] – the maximum amount of score our opponent gets from the subarray [i … (j-1)].
This can be solved using the simple Dynamic Programming relation given above. The final answer would be contained in dp[0][n-1].
However, we still need to account for the impact of introducing the negative score.
Suppose dp[0][n-1] equals VAL, the sum of all the scores equals SUM, and the total score of our opponent equals OPP,
- Then according to the original problem we are supposed to calculate abs(OPP) + VAL since our opponent does not have any negative impact on our final answer according to the original problem statement.
- This value can be easily calculated as,
VAL + 2*abs(OPP) = SUM
(OPP removed by our opponent implies that we had gained OPP amount as well, hence the 2*abs(OPP))
=> VAL + abs(OPP) = (SUM + VAL)/2
The implementation of the above approach is given below.
C++
#include <bits/stdc++.h>
using namespace std;
long long maximumAmount(int arr[], int n)
{
long long sum = 0;
vector<vector<long long> > dp(n,vector<long long>(n, 0));
for (int i = (n - 1); i >= 0; i--) {
sum += arr[i];
for (int j = i; j < n; j++) {
if (i == j) {
dp[i][j] = arr[i];
}
else {
dp[i][j] = max(arr[i] - dp[i + 1][j],
arr[j] - dp[i][j - 1]);
}
}
}
return (sum + dp[0][n - 1]) / 2;
}
int main()
{
int arr1[] = { 8, 15, 3, 7 };
int n = sizeof(arr1) / sizeof(arr1[0]);
printf("%lld\n", maximumAmount(arr1, n));
return 0;
}
|
Java
import java.util.*;
class GFG {
static long maximumAmount(int arr[], int n)
{
long sum = 0;
long dp[][] = new long[n][n];
for (int i = (n - 1); i >= 0; i--) {
sum += arr[i];
for (int j = i; j < n; j++) {
if (i == j) {
dp[i][j] = arr[i];
}
else {
dp[i][j] = Math.max(arr[i] - dp[i + 1][j],arr[j] - dp[i][j - 1]);
}
}
}
return (sum + dp[0][n - 1]) / 2;
}
public static void main (String[] args) {
int arr1[] = { 8, 15, 3, 7 };
int n = arr1.length;
System.out.println(maximumAmount(arr1, n));
}
}
|
Python3
import math
def maximumAmount(arr, n):
sum = 0;
dp=[[0]*n for _ in range(n)];
for i in range(n-1, -1, -1):
sum += arr[i];
for j in range(i,n):
if (i == j):
dp[i][j] = arr[i];
else :
dp[i][j] = max(arr[i] - dp[i + 1][j],
arr[j] - dp[i][j - 1]);
return math.floor((sum + dp[0][n - 1]) / 2);
arr1 = [ 8, 15, 3, 7 ];
n = len(arr1);
print(maximumAmount(arr1, n));
|
C#
using System;
public class GFG {
static long maximumAmount(int[] arr, int n)
{
long sum = 0;
long[,] dp = new long[n, n];
for (int i = (n - 1); i >= 0; i--)
{
sum += arr[i];
for (int j = i; j < n; j++)
{
if (i == j)
{
dp[i, j] = arr[i];
}
else
{
dp[i, j] = Math.Max(arr[i] - dp[i + 1, j],
arr[j] - dp[i, j - 1]);
}
}
}
return (sum + dp[0, n - 1]) / 2;
}
public static void Main()
{
int[] arr1 = { 8, 15, 3, 7 };
int n = arr1.Length;
Console.WriteLine(maximumAmount(arr1, n));
}
}
|
Javascript
function maximumAmount(arr, n)
{
let sum = 0;
let dp= new Array(n);
for(let i = 0; i < n; i++)
dp[i] = new Array(n).fill(0);
for (let i = (n - 1); i >= 0; i--) {
sum += arr[i];
for (let j = i; j < n; j++) {
if (i == j) {
dp[i][j] = arr[i];
}
else
{
dp[i][j] = Math.max(arr[i] - dp[i + 1][j],
arr[j] - dp[i][j - 1]);
}
}
}
return (sum + dp[0][n - 1]) / 2;
}
let arr1 = [ 8, 15, 3, 7 ];
let n = arr1.length;
console.log(maximumAmount(arr1, n));
|
Time Complexity : O(n^2)
Space Complexity : O(n^2),
Efficient approach : Space optimization
In previous approach the current value dp[i][j] is only depend upon the current and previous row values of DP. So to optimize the space complexity we use a single 1D array to store the computations.
Implementation steps:
- Create a 1D vector dp of size n.
- Set a base case by initializing the values of DP .
- Now iterate over subproblems by the help of nested loop and get the current value from previous computations.
- At last return final answer (sum + dp[n – 1]) / 2.
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
long long maximumAmount(int arr[], int n)
{
long long sum = 0;
vector<long long> dp(n, 0);
for (int i = (n - 1); i >= 0; i--) {
sum += arr[i];
for (int j = i; j < n; j++) {
if (i == j) {
dp[j] = arr[j];
}
else {
dp[j] = max(arr[i] - dp[j],
arr[j] - dp[j - 1]);
}
}
}
return (sum + dp[n - 1]) / 2;
}
int main()
{
int arr1[] = { 8, 15, 3, 7 };
int n = sizeof(arr1) / sizeof(arr1[0]);
printf("%lld\n", maximumAmount(arr1, n));
return 0;
}
|
Java
import java.util.*;
public class Main {
public static long maximumAmount(int[] arr, int n)
{
long sum = 0;
long[] dp = new long[n];
Arrays.fill(dp, 0);
for (int i = (n - 1); i >= 0; i--) {
sum += arr[i];
for (int j = i; j < n; j++) {
if (i == j) {
dp[j] = arr[j];
}
else {
dp[j] = Math.max(arr[i] - dp[j],
arr[j] - dp[j - 1]);
}
}
}
return (sum + dp[n - 1]) / 2;
}
public static void main(String[] args)
{
int[] arr1 = { 8, 15, 3, 7 };
int n = arr1.length;
System.out.println(maximumAmount(arr1, n));
}
}
|
Python3
def maximumAmount(arr, n):
sum = 0
dp = [0] * n
for i in range(n - 1, -1, -1):
sum += arr[i]
for j in range(i, n):
if i == j:
dp[j] = arr[j]
else:
dp[j] = max(arr[i] - dp[j], arr[j] - dp[j - 1])
return (sum + dp[n - 1]) // 2
arr1 = [8, 15, 3, 7]
n = len(arr1)
print(maximumAmount(arr1, n))
|
C#
using System;
class GFG
{
static long maximumAmount(int[] arr, int n)
{
long sum = 0;
long[] dp = new long[n];
for (int i = (n - 1); i >= 0; i--) {
sum += arr[i];
for (int j = i; j < n; j++) {
if (i == j) {
dp[j] = arr[j];
}
else {
dp[j] = Math.Max(arr[i] - dp[j],
arr[j] - dp[j - 1]);
}
}
}
return (sum + dp[n - 1]) / 2;
}
static void Main()
{
int[] arr1 = { 8, 15, 3, 7 };
int n = arr1.Length;
Console.WriteLine(maximumAmount(arr1, n));
}
}
|
Javascript
function maximumAmount(arr, n)
{
let sum = 0;
let dp = new Array(n).fill(0);
for (let i = (n - 1); i >= 0; i--) {
sum += arr[i];
for (let j = i; j < n; j++) {
if (i == j) {
dp[j] = arr[j];
}
else {
dp[j] = Math.max(arr[i] - dp[j],
arr[j] - dp[j - 1]);
}
}
}
return Math.floor(sum + dp[n - 1]) / 2;
}
let arr1 = [ 8, 15, 3, 7 ];
let n = arr1.length;
console.log(maximumAmount(arr1, n));
|
Output
22
Time Complexity : O(n^2)
Space Complexity : O(n),
This approach is suggested by Ojassvi Kumar.
Share your thoughts in the comments
Please Login to comment...