Skip to content
Related Articles

Related Articles

Optimal Strategy for a Game | DP-31

View Discussion
Improve Article
Save Article
  • Difficulty Level : Hard
  • Last Updated : 20 Jul, 2022

Consider a row of n coins of values v1 . . . vn, where n is even. We play a game against an opponent by alternating turns. In each turn, a player selects either the first or last coin from the row, removes it from the row permanently, and receives the value of the coin. Determine the maximum possible amount of money we can definitely win if we move first.
Note: The opponent is as clever as the user.

Let us understand the problem with few examples:  

  1. 5, 3, 7, 10 : The user collects maximum value as 15(10 + 5)
  2. 8, 15, 3, 7 : The user collects maximum value as 22(7 + 15)

Does choosing the best at each move gives an optimal solution? No. 
In the second example, this is how the game can be finished:

  1. …….User chooses 8. 
    …….Opponent chooses 15. 
    …….User chooses 7. 
    …….Opponent chooses 3. 
    Total value collected by user is 15(8 + 7)
  2. …….User chooses 7. 
    …….Opponent chooses 8. 
    …….User chooses 15. 
    …….Opponent chooses 3. 
    Total value collected by user is 22(7 + 15)

So if the user follows the second game state, the maximum value can be collected although the first move is not the best. 

Approach: As both the players are equally strong, both will try to reduce the possibility of winning of each other. Now let’s see how the opponent can achieve this.

There are two choices:  

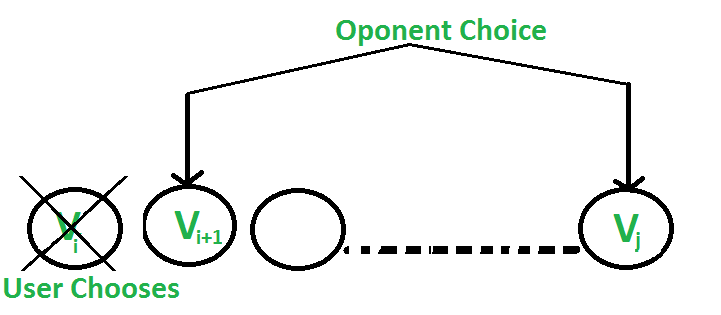
  • The user chooses the ‘ith’ coin with value ‘Vi’: The opponent either chooses (i+1)th coin or jth coin. The opponent intends to choose the coin which leaves the user with minimum value. 
    i.e. The user can collect the value Vi + min(F(i+2, j), F(i+1, j-1) ) where [i+2,j] is the range of array indices available to the user if the opponent chooses Vi+1 and [i+1,j-1] is the range of array indexes available if opponent chooses the jth coin. 

coinGame1

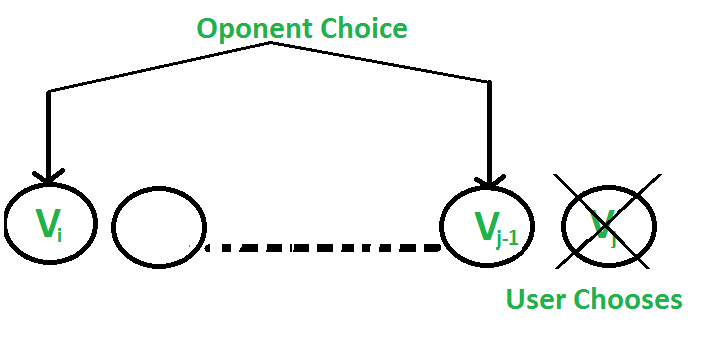
  • The user chooses the ‘jth’ coin with value ‘Vj’: The opponent either chooses ‘ith’ coin or ‘(j-1)th’ coin. The opponent intends to choose the coin which leaves the user with minimum value, i.e. the user can collect the value Vj + min(F(i+1, j-1), F(i, j-2) ) where [i,j-2] is the range of array indices available for the user if the opponent picks jth coin and [i+1,j-1] is the range of indices available to the user if the opponent picks up the ith coin.
     

coinGame2

Following is the recursive solution that is based on the above two choices. We take a maximum of two choices. 

F(i, j) represents the maximum value the user
can collect from i'th coin to j'th coin.

F(i, j) = Max(Vi + min(F(i+2, j), F(i+1, j-1) ), 
              Vj + min(F(i+1, j-1), F(i, j-2) ))
As user wants to maximise the number of coins. 

Base Cases
    F(i, j) = Vi           If j == i
    F(i, j) = max(Vi, Vj)  If j == i + 1

The recursive top down solution in is shown below

C++




// C++ code to implement the approach
 
#include <bits/stdc++.h>
 
using namespace std;
 
vector<int> arr;
map<vector<int>, int> memo;
int n = arr.size();
 
// recursive top down memoized solution
int solve(int i, int j)
{
    if ((i > j) || (i >= n) || (j < 0))
        return 0;
 
    vector<int> k{ i, j };
    if (memo[k] != 0)
        return memo[k];
 
    // if the user chooses ith coin, the opponent can choose
    // from i+1th or jth coin. if he chooses i+1th coin,
    // user is left with [i+2,j] range. if opp chooses jth
    // coin, then user is left with [i+1,j-1] range to
    // choose from. Also opponent tries to choose in such a
    // way that the user has minimum value left.
    int option1
        = arr[i]
          + min(solve(i + 2, j), solve(i + 1, j - 1));
 
    // if user chooses jth coin, opponent can choose ith
    // coin or j-1th coin. if opp chooses ith coin,user can
    // choose in range [i+1,j-1]. if opp chooses j-1th coin,
    // user can choose in range [i,j-2].
    int option2
        = arr[j]
          + min(solve(i + 1, j - 1), solve(i, j - 2));
 
    // since the user wants to get maximum money
    memo[k] = max(option1, option2);
    return memo[k];
}
 
int optimalStrategyOfGame()
{
 
    memo.clear();
    return solve(0, n - 1);
}
 
// Driver code
int main()
{
    arr.push_back(8);
    arr.push_back(15);
    arr.push_back(3);
    arr.push_back(7);
    n = arr.size();
    cout << optimalStrategyOfGame() << endl;
 
    arr.clear();
    arr.push_back(2);
    arr.push_back(2);
    arr.push_back(2);
    arr.push_back(2);
    n = arr.size();
    cout << optimalStrategyOfGame() << endl;
 
    arr.clear();
    arr.push_back(20);
    arr.push_back(30);
    arr.push_back(2);
    arr.push_back(2);
    arr.push_back(2);
    arr.push_back(10);
    n = arr.size();
    cout << optimalStrategyOfGame() << endl;
}
 
// This code is contributed by phasing17

Java



// Java code to implement the approach
import java.util.*;
 
class GFG {
    static ArrayList<Integer> arr = new ArrayList<>();
    static HashMap<ArrayList<Integer>, Integer> memo
        = new HashMap<>();
    static int n = 0;
 
    // recursive top down memoized solution
    static int solve(int i, int j)
    {
        if ((i > j) || (i >= n) || (j < 0))
            return 0;
 
        ArrayList<Integer> k = new ArrayList<Integer>();
        k.add(i);
        k.add(j);
        if (memo.containsKey(k))
            return memo.get(k);
 
        // if the user chooses ith coin, the opponent can
        // choose from i+1th or jth coin. if he chooses
        // i+1th coin, user is left with [i+2,j] range. if
        // opp chooses jth coin, then user is left with
        // [i+1,j-1] range to choose from. Also opponent
        // tries to choose in such a way that the user has
        // minimum value left.
        int option1 = arr.get(i)
                      + Math.min(solve(i + 2, j),
                                 solve(i + 1, j - 1));
 
        // if user chooses jth coin, opponent can choose ith
        // coin or j-1th coin. if opp chooses ith coin,user
        // can choose in range [i+1,j-1]. if opp chooses
        // j-1th coin, user can choose in range [i,j-2].
        int option2 = arr.get(j)
                      + Math.min(solve(i + 1, j - 1),
                                 solve(i, j - 2));
 
        // since the user wants to get maximum money
        memo.put(k, Math.max(option1, option2));
        return memo.get(k);
    }
 
    static int optimalStrategyOfGame()
    {
 
        memo.clear();
        return solve(0, n - 1);
    }
 
    // Driver code
    public static void main(String[] args)
    {
        arr.add(8);
        arr.add(15);
        arr.add(3);
        arr.add(7);
        n = arr.size();
        System.out.println(optimalStrategyOfGame());
 
        arr.clear();
        arr.add(2);
        arr.add(2);
        arr.add(2);
        arr.add(2);
        n = arr.size();
        System.out.println(optimalStrategyOfGame());
 
        arr.clear();
        arr.add(20);
        arr.add(30);
        arr.add(2);
        arr.add(2);
        arr.add(2);
        arr.add(10);
        n = arr.size();
        System.out.println(optimalStrategyOfGame());
    }
}
 
// This code is contributed by phasing17
Python3



def optimalStrategyOfGame(arr, n):
    memo = {}
 
    # recursive top down memoized solution
    def solve(i, j):
        if i > j or i >= n or j < 0:
            return 0
 
        k = (i, j)
        if k in memo:
            return memo[k]
 
        # if the user chooses ith coin, the opponent can choose from i+1th or jth coin.
        # if he chooses i+1th coin, user is left with [i+2,j] range.
        # if opp chooses jth coin, then user is left with [i+1,j-1] range to choose from.
        # Also opponent tries to choose
        # in such a way that the user has minimum value left.
        option1 = arr[i] + min(solve(i+2, j), solve(i+1, j-1))
 
        # if user chooses jth coin, opponent can choose ith coin or j-1th coin.
        # if opp chooses ith coin,user can choose in range [i+1,j-1].
        # if opp chooses j-1th coin, user can choose in range [i,j-2].
        option2 = arr[j] + min(solve(i+1, j-1), solve(i, j-2))
 
        # since the user wants to get maximum money
        memo[k] = max(option1, option2)
        return memo[k]
 
    return solve(0, n-1)
C#



// C# code to implement the approach
using System;
using System.Collections.Generic;
 
class GFG {
  static List<int> arr = new List<int>();
  static Dictionary<List<int>, int> memo
    = new Dictionary<List<int>, int>();
  static int n = 0;
 
  // recursive top down memoized solution
  static int solve(int i, int j)
  {
    if ((i > j) || (i >= n) || (j < 0))
      return 0;
 
    List<int> k = new List<int>{ i, j };
    if (memo.ContainsKey(k))
      return memo[k];
 
    // if the user chooses ith coin, the opponent can
    // choose from i+1th or jth coin. if he chooses
    // i+1th coin, user is left with [i+2,j] range. if
    // opp chooses jth coin, then user is left with
    // [i+1,j-1] range to choose from. Also opponent
    // tries to choose in such a way that the user has
    // minimum value left.
    int option1 = arr[i]
      + Math.Min(solve(i + 2, j),
                 solve(i + 1, j - 1));
 
    // if user chooses jth coin, opponent can choose ith
    // coin or j-1th coin. if opp chooses ith coin,user
    // can choose in range [i+1,j-1]. if opp chooses
    // j-1th coin, user can choose in range [i,j-2].
    int option2 = arr[j]
      + Math.Min(solve(i + 1, j - 1),
                 solve(i, j - 2));
 
    // since the user wants to get maximum money
    memo[k] = Math.Max(option1, option2);
    return memo[k];
  }
 
  static int optimalStrategyOfGame()
  {
 
    memo.Clear();
    return solve(0, n - 1);
  }
 
  // Driver code
  public static void Main(string[] args)
  {
    arr.Add(8);
    arr.Add(15);
    arr.Add(3);
    arr.Add(7);
    n = arr.Count;
    Console.WriteLine(optimalStrategyOfGame());
 
    arr.Clear();
    arr.Add(2);
    arr.Add(2);
    arr.Add(2);
    arr.Add(2);
    n = arr.Count;
    Console.WriteLine(optimalStrategyOfGame());
 
    arr.Clear();
    arr.Add(20);
    arr.Add(30);
    arr.Add(2);
    arr.Add(2);
    arr.Add(2);
    arr.Add(10);
    n = arr.Count;
    Console.WriteLine(optimalStrategyOfGame());
  }
}
 
// This code is contributed by phasing17
Javascript



// JavaScript code to implement the approach
 
function optimalStrategyOfGame(arr, n)
{
 
    let memo = {};
 
    // recursive top down memoized solution
    function solve(i, j)
    {
        if ( (i > j) || (i >= n) || (j < 0))
            return 0;
 
        let k = (i, j);
        if (memo.hasOwnProperty(k))
            return memo[k];
 
        // if the user chooses ith coin, the opponent can choose from i+1th or jth coin.
        // if he chooses i+1th coin, user is left with [i+2,j] range.
        // if opp chooses jth coin, then user is left with [i+1,j-1] range to choose from.
        // Also opponent tries to choose
        // in such a way that the user has minimum value left.
        let option1 = arr[i] + Math.min(solve(i+2, j), solve(i+1, j-1));
 
        // if user chooses jth coin, opponent can choose ith coin or j-1th coin.
        // if opp chooses ith coin,user can choose in range [i+1,j-1].
        // if opp chooses j-1th coin, user can choose in range [i,j-2].
        let option2 = arr[j] + Math.min(solve(i+1, j-1), solve(i, j-2));
 
        // since the user wants to get maximum money
        memo[k] = Math.max(option1, option2);
        return memo[k];
    }
 
    return solve(0, n-1);
}
 
 
// Driver code
let arr1 = [ 8, 15, 3, 7 ];
let n = arr1.length;
console.log(optimalStrategyOfGame(arr1, n));
 
let arr2 = [ 2, 2, 2, 2 ];
n = arr2.length;
console.log(optimalStrategyOfGame(arr2, n));
 
 
let arr3 = [ 20, 30, 2, 2, 2, 10 ];
n = arr3.length;
console.log(optimalStrategyOfGame(arr3, n));
 
 
 
// This code is contributed by phasing17
The bottom up approach is shown below.
C++



// C++ program to find out
// maximum value from a given
// sequence of coins
#include <bits/stdc++.h>
using namespace std;
 
// Returns optimal value possible
// that a player can collect from
// an array of coins of size n.
// Note than n must be even
int optimalStrategyOfGame(int* arr, int n)
{
    // Create a table to store
    // solutions of subproblems
    int table[n][n];
 
    // Fill table using above
    // recursive formula. Note
    // that the table is filled
    // in diagonal fashion (similar
    // to http:// goo.gl/PQqoS),
    // from diagonal elements to
    // table[0][n-1] which is the result.
    for (int gap = 0; gap < n; ++gap) {
        for (int i = 0, j = gap; j < n; ++i, ++j) {
            // Here x is value of F(i+2, j),
            // y is F(i+1, j-1) and
            // z is F(i, j-2) in above recursive
            // formula
            int x = ((i + 2) <= j) ? table[i + 2][j] : 0;
            int y = ((i + 1) <= (j - 1))
                        ? table[i + 1][j - 1]
                        : 0;
            int z = (i <= (j - 2)) ? table[i][j - 2] : 0;
 
            table[i][j] = max(arr[i] + min(x, y),
                              arr[j] + min(y, z));
        }
    }
 
    return table[0][n - 1];
}
 
// Driver program to test above function
int main()
{
    int arr1[] = { 8, 15, 3, 7 };
    int n = sizeof(arr1) / sizeof(arr1[0]);
    printf("%d\n", optimalStrategyOfGame(arr1, n));
 
    int arr2[] = { 2, 2, 2, 2 };
    n = sizeof(arr2) / sizeof(arr2[0]);
    printf("%d\n", optimalStrategyOfGame(arr2, n));
 
    int arr3[] = { 20, 30, 2, 2, 2, 10 };
    n = sizeof(arr3) / sizeof(arr3[0]);
    printf("%d\n", optimalStrategyOfGame(arr3, n));
 
    return 0;
}
Java



// Java program to find out maximum
// value from a given sequence of coins
import java.io.*;
 
class GFG {
 
    // Returns optimal value possible
    // that a player can collect from
    // an array of coins of size n.
    // Note than n must be even
    static int optimalStrategyOfGame(int arr[], int n)
    {
        // Create a table to store
        // solutions of subproblems
        int table[][] = new int[n][n];
        int gap, i, j, x, y, z;
 
        // Fill table using above recursive formula.
        // Note that the tableis filled in diagonal
        // fashion (similar to http:// goo.gl/PQqoS),
        // from diagonal elements to table[0][n-1]
        // which is the result.
        for (gap = 0; gap < n; ++gap) {
            for (i = 0, j = gap; j < n; ++i, ++j) {
 
                // Here x is value of F(i+2, j),
                // y is F(i+1, j-1) and z is
                // F(i, j-2) in above recursive formula
                x = ((i + 2) <= j) ? table[i + 2][j] : 0;
                y = ((i + 1) <= (j - 1))
                        ? table[i + 1][j - 1]
                        : 0;
                z = (i <= (j - 2)) ? table[i][j - 2] : 0;
 
                table[i][j]
                    = Math.max(arr[i] + Math.min(x, y),
                               arr[j] + Math.min(y, z));
            }
        }
 
        return table[0][n - 1];
    }
 
    // Driver program
    public static void main(String[] args)
    {
        int arr1[] = { 8, 15, 3, 7 };
        int n = arr1.length;
        System.out.println(
            "" + optimalStrategyOfGame(arr1, n));
 
        int arr2[] = { 2, 2, 2, 2 };
        n = arr2.length;
        System.out.println(
            "" + optimalStrategyOfGame(arr2, n));
 
        int arr3[] = { 20, 30, 2, 2, 2, 10 };
        n = arr3.length;
        System.out.println(
            "" + optimalStrategyOfGame(arr3, n));
    }
}
 
// This code is contributed by vt_m
Python3



# Python3 program to find out maximum
# value from a given sequence of coins
 
# Returns optimal value possible that
# a player can collect from an array
# of coins of size n. Note than n
# must be even
 
 
def optimalStrategyOfGame(arr, n):
 
    # Create a table to store
    # solutions of subproblems
    table = [[0 for i in range(n)]
             for i in range(n)]
 
    # Fill table using above recursive
    # formula. Note that the table is
    # filled in diagonal fashion
    # (similar to http://goo.gl / PQqoS),
    # from diagonal elements to
    # table[0][n-1] which is the result.
    for gap in range(n):
        for j in range(gap, n):
            i = j - gap
 
            # Here x is value of F(i + 2, j),
            # y is F(i + 1, j-1) and z is
            # F(i, j-2) in above recursive
            # formula
            x = 0
            if((i + 2) <= j):
                x = table[i + 2][j]
            y = 0
            if((i + 1) <= (j - 1)):
                y = table[i + 1][j - 1]
            z = 0
            if(i <= (j - 2)):
                z = table[i][j - 2]
            table[i][j] = max(arr[i] + min(x, y),
                              arr[j] + min(y, z))
    return table[0][n - 1]
 
 
# Driver Code
arr1 = [8, 15, 3, 7]
n = len(arr1)
print(optimalStrategyOfGame(arr1, n))
 
arr2 = [2, 2, 2, 2]
n = len(arr2)
print(optimalStrategyOfGame(arr2, n))
 
arr3 = [20, 30, 2, 2, 2, 10]
n = len(arr3)
print(optimalStrategyOfGame(arr3, n))
 
# This code is contributed
# by sahilshelangia
C#



// C# program to find out maximum
// value from a given sequence of coins
using System;
 
public class GFG {
 
    // Returns optimal value possible that a player
    // can collect from an array of coins of size n.
    // Note than n must be even
    static int optimalStrategyOfGame(int[] arr, int n)
    {
        // Create a table to store solutions of subproblems
        int[, ] table = new int[n, n];
        int gap, i, j, x, y, z;
 
        // Fill table using above recursive formula.
        // Note that the tableis filled in diagonal
        // fashion (similar to http:// goo.gl/PQqoS),
        // from diagonal elements to table[0][n-1]
        // which is the result.
        for (gap = 0; gap < n; ++gap) {
            for (i = 0, j = gap; j < n; ++i, ++j) {
 
                // Here x is value of F(i+2, j),
                // y is F(i+1, j-1) and z is
                // F(i, j-2) in above recursive formula
                x = ((i + 2) <= j) ? table[i + 2, j] : 0;
                y = ((i + 1) <= (j - 1))
                        ? table[i + 1, j - 1]
                        : 0;
                z = (i <= (j - 2)) ? table[i, j - 2] : 0;
 
                table[i, j]
                    = Math.Max(arr[i] + Math.Min(x, y),
                               arr[j] + Math.Min(y, z));
            }
        }
 
        return table[0, n - 1];
    }
 
    // Driver program
 
    static public void Main()
    {
        int[] arr1 = { 8, 15, 3, 7 };
        int n = arr1.Length;
        Console.WriteLine(""
                          + optimalStrategyOfGame(arr1, n));
 
        int[] arr2 = { 2, 2, 2, 2 };
        n = arr2.Length;
        Console.WriteLine(""
                          + optimalStrategyOfGame(arr2, n));
 
        int[] arr3 = { 20, 30, 2, 2, 2, 10 };
        n = arr3.Length;
        Console.WriteLine(""
                          + optimalStrategyOfGame(arr3, n));
    }
}
 
// This code is contributed by ajit
PHP



<?php
// PHP program to find out maximum value
// from a given sequence of coins
 
// Returns optimal value possible that a
// player can collect from an array of
// coins of size n. Note than n must be even
function optimalStrategyOfGame($arr, $n)
{
    // Create a table to store solutions
    // of subproblems
    $table = array_fill(0, $n,
             array_fill(0, $n, 0));
 
    // Fill table using above recursive formula.
    // Note that the table is filled in diagonal
    // fashion (similar to http://goo.gl/PQqoS),
    // from diagonal elements to table[0][n-1]
    // which is the result.
    for ($gap = 0; $gap < $n; ++$gap)
    {
        for ($i = 0, $j = $gap; $j < $n; ++$i, ++$j)
        {
 
            // Here x is value of F(i+2, j),
            // y is F(i+1, j-1) and z is F(i, j-2)
            // in above recursive formula
            $x = (($i + 2) <= $j) ?
               $table[$i + 2][$j] : 0;
            $y = (($i + 1) <= ($j - 1)) ?
                 $table[$i + 1][$j - 1] : 0;
            $z = ($i <= ($j - 2)) ?
               $table[$i][$j - 2] : 0;
 
            $table[$i][$j] = max($arr[$i] + min($x, $y),
                                 $arr[$j] + min($y, $z));
        }
    }
 
    return $table[0][$n - 1];
}
 
// Driver Code
$arr1 = array( 8, 15, 3, 7 );
$n = count($arr1);
print(optimalStrategyOfGame($arr1, $n) . "\n");
 
$arr2 = array( 2, 2, 2, 2 );
$n = count($arr2);
print(optimalStrategyOfGame($arr2, $n) . "\n");
 
$arr3 = array(20, 30, 2, 2, 2, 10);
$n = count($arr3);
print(optimalStrategyOfGame($arr3, $n) . "\n");
 
// This code is contributed by chandan_jnu
?>
Javascript



<script>
 
// Javascript program to find out maximum
// value from a given sequence of coins
 
// Returns optimal value possible
// that a player can collect from
// an array of coins of size n.
// Note than n must be even
function optimalStrategyOfGame(arr, n)
{
     
    // Create a table to store
    // solutions of subproblems
    let table = new Array(n);
    let gap, i, j, x, y, z;
     
    for(let d = 0; d < n; d++)
    {
        table[d] = new Array(n);
    }
 
    // Fill table using above recursive formula.
    // Note that the tableis filled in diagonal
    // fashion (similar to http:// goo.gl/PQqoS),
    // from diagonal elements to table[0][n-1]
    // which is the result.
    for(gap = 0; gap < n; ++gap)
    {
        for(i = 0, j = gap; j < n; ++i, ++j)
        {
             
            // Here x is value of F(i+2, j),
            // y is F(i+1, j-1) and z is
            // F(i, j-2) in above recursive formula
            x = ((i + 2) <= j) ? table[i + 2][j] : 0;
            y = ((i + 1) <= (j - 1)) ?
            table[i + 1][j - 1] : 0;
            z = (i <= (j - 2)) ? table[i][j - 2] : 0;
 
            table[i][j] = Math.max(
                arr[i] + Math.min(x, y),
                arr[j] + Math.min(y, z));
        }
    }
    return table[0][n - 1];
}
 
// Driver code
let arr1 = [ 8, 15, 3, 7 ];
let n = arr1.length;
document.write("" + optimalStrategyOfGame(arr1, n) +
               "</br>");
 
let arr2 = [ 2, 2, 2, 2 ];
n = arr2.length;
document.write("" + optimalStrategyOfGame(arr2, n) +
               "</br>");
 
let arr3 = [ 20, 30, 2, 2, 2, 10 ];
n = arr3.length;
document.write("" + optimalStrategyOfGame(arr3, n));
   
// This code is contributed by divyesh072019
 
</script>
Output
22
4
42
Complexity Analysis: 
  • Time Complexity: O(n2). 
    Use of a nested for loop brings the time complexity to n2.
  • Auxiliary Space: O(n2). 
    As a 2-D table is used for storing states.
Note: The above solution can be optimized by using less number of comparisons for every choice. Please refer below. 
Optimal Strategy for a Game | Set 2
Exercise: 
Your thoughts on the strategy when the user wishes to only win instead of winning with the maximum value. Like the above problem, the number of coins is even. 
Can the Greedy approach work quite well and give an optimal solution? Will your answer change if the number of coins is odd? Please see Coin game of two corners
This article is compiled by Aashish Barnwal. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above
 

My Personal Notes
arrow_drop_up
Previous
Optimal Strategy for a Game | Set 2
Next

Top 20 Dynamic Programming Interview Questions
Recommended Articles
Page :
Game Theory (Normal form game) | Set 2 (Game with Pure Strategy)
31, Jul 19
Game Theory (Normal-form game) | Set 3 (Game with Mixed Strategy)
02, Aug 19
Optimal Strategy for a Game | Set 3
17, Sep 19
Optimal strategy for a Game with modifications
02, Jan 20
Optimal Strategy for the Divisor game using Dynamic Programming
26, Apr 20
Optimal Strategy for a Game | Set 2
14, May 19
Optimal Strategy for a Game | Special Gold Coin
26, Nov 19
Game Theory (Normal-form Game) | Set 4 (Dominance Property-Pure Strategy)
10, Dec 19
Game Theory (Normal-form Game) | Set 5 (Dominance Property-Mixed Strategy)
10, Dec 19
Game Theory (Normal-form Game) | Set 6 (Graphical Method [2 X N] Game)
18, Dec 19
Game Theory (Normal-form Game) | Set 7 (Graphical Method [M X 2] Game)
18, Dec 19
Minimax Algorithm in Game Theory | Set 3 (Tic-Tac-Toe AI - Finding optimal move)
30, Jun 16
Game Theory (Normal - form game) | Set 1 (Introduction)
30, Jul 19
Combinatorial Game Theory | Set 2 (Game of Nim)
21, May 16
Find optimal weights which can be used to weigh all the weights in the range [1, X]
20, Jun 19
Optimal Substructure Property in Dynamic Programming | DP-2
03, Jun 11
Secretary Problem (A Optimal Stopping Problem)
20, Oct 17
Optimal Binary Search Tree | DP-24
14, Dec 12
Combinatorial Game Theory | Set 3 (Grundy Numbers/Numbers and Mex)
06, Jun 16
Combinatorial Game Theory | Set 4 (Sprague - Grundy Theorem)
07, Jun 16
Minimax Algorithm in Game Theory | Set 2 (Introduction to Evaluation Function)
21, Jun 16
Implementation of Tic-Tac-Toe game
30, Jun 16
Minimax Algorithm in Game Theory | Set 4 (Alpha-Beta Pruning)
24, Jul 16
Minimax Algorithm in Game Theory | Set 5 (Zobrist Hashing)
10, Oct 16
Article Contributed By :
https://media.geeksforgeeks.org/auth/avatar.png
GeeksforGeeks
Vote for difficulty
Current difficulty :
Hard





Improved By :
Article Tags :
Practice Tags :
Report Issue

We use cookies to ensure you have the best browsing experience on our website. By using our site, you
acknowledge that you have read and understood our
Cookie Policy &
        Privacy Policy

Lightbox

Start Your Coding Journey Now!