Number of unique permutations starting with 1 of a Binary String
Last Updated :
06 Apr, 2023
Given a binary string composed of 0’s and 1’s. The task is to find the number of unique permutation of the string which starts with 1.
Note: Since the answer can be very large, print the answer under modulo 109 + 7.
Examples:
Input : str ="10101001001"
Output : 210
Input : str ="101110011"
Output : 56
The idea is to first find the count of 1’s and the count of 0’s in the given string. Now let us consider that the string is of length 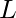 and the string consists of at least one 1. Let the number of 1’s be
and the string consists of at least one 1. Let the number of 1’s be 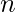 and the number of 0’s be
and the number of 0’s be 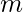 . Out of n number of 1’s we have to place one 1 at the beginning of the string so we have n-1 1’s left and m 0’s we have to permute these (n-1) 1’s and m 0’s in length (L-1) of the string.
. Out of n number of 1’s we have to place one 1 at the beginning of the string so we have n-1 1’s left and m 0’s we have to permute these (n-1) 1’s and m 0’s in length (L-1) of the string.
Therefore, the number of permutation will be:
(L-1)! / ((n-1)!*(m)!)
Below is the implementation of the above idea:
C++
#include <bits/stdc++.h>
using namespace std;
#define MAX 1000003
#define mod 1000000007
long long fact[MAX];
void factorial()
{
fact[0] = 1;
for (int i = 1; i < MAX; i++) {
fact[i] = (fact[i - 1] * i) % mod;
}
}
long long power(long long x, long long y, long long p)
{
long long res = 1;
x = x % p;
while (y > 0) {
if (y & 1)
res = (res * x) % p;
y = y >> 1;
x = (x * x) % p;
}
return res;
}
long long inverse(int n)
{
return power(n, mod - 2, mod);
}
int countPermutation(string s)
{
factorial();
int length = s.length(), num1 = 0, num0;
long long count = 0;
for (int i = 0; i < length; i++) {
if (s[i] == '1')
num1++;
}
num0 = length - num1;
count = (fact[length - 1] *
inverse((fact[num1 - 1] *
fact[num0]) % mod)) % mod;
return count;
}
int main()
{
string str = "10101001001";
cout << countPermutation(str);
return 0;
}
|
Java
public class Improve {
final static int MAX = 1000003 ;
final static int mod = 1000000007 ;
static long fact[] = new long [MAX];
static void factorial()
{
fact[0] = 1;
for (int i = 1; i < MAX; i++) {
fact[i] = (fact[i - 1] * i) % mod;
}
}
static long power(long x, long y, long p)
{
long res = 1;
x = x % p;
while (y > 0) {
if (y % 2 != 0)
res = (res * x) % p;
y = y >> 1;
x = (x * x) % p;
}
return res;
}
static long inverse(int n)
{
return power(n, mod - 2, mod);
}
static int countPermutation(String s)
{
factorial();
int length = s.length(), num1 = 0, num0;
long count = 0;
for (int i = 0; i < length; i++) {
if (s.charAt(i) == '1')
num1++;
}
num0 = length - num1;
count = (fact[length - 1] *
inverse((int) ((fact[num1 - 1] *
fact[num0]) % mod))) % mod;
return (int) count;
}
public static void main(String args[])
{
String str = "10101001001";
System.out.println(countPermutation(str));
}
}
|
Python 3
MAX = 1000003
mod = 1000000007
fact = [0] * MAX
def factorial():
fact[0] = 1
for i in range(1, MAX):
fact[i] = (fact[i - 1] * i) % mod
def power(x, y, p):
res = 1
x = x % p
while (y > 0) :
if (y & 1):
res = (res * x) % p
y = y >> 1
x = (x * x) % p
return res
def inverse( n):
return power(n, mod - 2, mod)
def countPermutation(s):
factorial()
length = len(s)
num1 = 0
count = 0
for i in range(length) :
if (s[i] == '1'):
num1 += 1
num0 = length - num1
count = (fact[length - 1] *
inverse((fact[num1 - 1] *
fact[num0]) % mod)) % mod
return count
if __name__ =="__main__":
s = "10101001001"
print(countPermutation(s))
|
C#
using System;
class GFG
{
static int MAX = 1000003 ;
static int mod = 1000000007 ;
static long []fact = new long [MAX];
static void factorial()
{
fact[0] = 1;
for (int i = 1; i < MAX; i++)
{
fact[i] = (fact[i - 1] * i) % mod;
}
}
static long power(long x,
long y, long p)
{
long res = 1;
x = x % p;
while (y > 0)
{
if (y % 2 != 0)
res = (res * x) % p;
y = y >> 1;
x = (x * x) % p;
}
return res;
}
static long inverse(int n)
{
return power(n, mod - 2, mod);
}
static int countPermutation(string s)
{
factorial();
int length = s.Length, num1 = 0, num0;
long count = 0;
for (int i = 0; i < length; i++)
{
if (s[i] == '1')
num1++;
}
num0 = length - num1;
count = (fact[length - 1] *
inverse((int) ((fact[num1 - 1] *
fact[num0]) % mod))) % mod;
return (int) count;
}
public static void Main()
{
string str = "10101001001";
Console.WriteLine(countPermutation(str));
}
}
|
Javascript
<script>
var MAX = 1000003
var mod = 100000007
var fact = Array(MAX);
function factorial()
{
fact[0] = 1;
for (var i = 1; i < MAX; i++) {
fact[i] = (fact[i - 1] * i) % mod;
}
}
function power(x, y, p)
{
var res = 1;
x = x % p;
while (y > 0) {
if (y & 1)
res = (res * x) % p;
y = y >> 1;
x = (x * x) % p;
}
return res;
}
function inverse(n)
{
return power(n, mod - 2, mod);
}
function countPermutation(s)
{
factorial();
var length = s.length, num1 = 0, num0;
var count = 0;
for (var i = 0; i < length; i++) {
if (s[i] == '1')
num1++;
}
// number of 0's
num0 = length - num1;
count = (fact[length - 1] *
inverse((fact[num1 - 1] *
fact[num0]) % mod)) % mod;
return count;
}
var str = "10101001001";
document.write( countPermutation(str));
</script>
|
Time Complexity: O(n), where n is the length of the string.
Auxilitary Space Complexity : O(n)
Share your thoughts in the comments
Please Login to comment...