Leaf starting point in a Binary Heap data structure
Last Updated :
21 Jul, 2022
Binary Heap is a complete tree (All levels are completely filled except possibly the last level and the last level has all keys as left as possible). In other words, we can say that it’s an almost complete binary tree. A Binary heap is typically represented as array. If we take a closer look, we can noticed that in a Heap with number of nodes n, the leaves start from a particular index and following it, all the nodes are leaves till index n. Let’s see an example to observe this:
10
/ \
20 100
/
30
Let us represent this in the form of an array Arr whose index starts from 1 : we have: Arr[1] = 10 Arr[2] = 20 Arr[3] = 100 Arr[4] = 30 If we observe, the first leaf (i.e. 100) starts from the index 3. Following it Arr[4] is also a leaf. By carefully analyzing, the following conclusion is observed:
The first leaf in a Heap starts from [floor(n/2)]+1 and all the nodes following it till n are leaves.
Conclusion: In a Heap having n elements, Elements from indexes [(floor(n/2)+1) to n] are leaves. What is starting index of leaves if indexes start from 0 instead of 1? The above explanation assumes indexes starting from 1, but in most of the programming languages, index starts with 0.
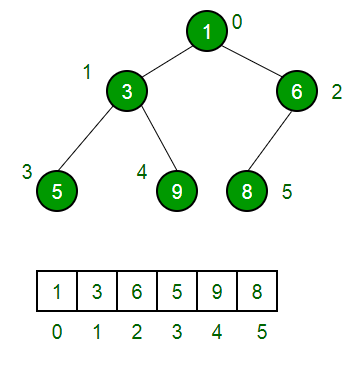
If we consider 0 as starting index, then leaves starts from floor(n/2) and exist till end, i.e., (n-1).
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...